梯度下降法,二维空间三维空间 代码实现
Posted ZhangJiQun.
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了梯度下降法,二维空间三维空间 代码实现相关的知识,希望对你有一定的参考价值。
目录
二维空间梯度下降法
机器学习算法常常可以归结为求解一个最优化问题,而梯度下降法就是求解最优化问题的一个方法。
梯度下降法(gradient descent)或最速下降法(steepest decent),是求解无约束最优化问题的一种最常用的方法。
梯度下降法实现简单,是一种迭代算法,每一步会求解目标函数的梯度向量。
问题定义
那么什么是目标函数,在机器学习中这常常是一个损失函数。不管怎么称呼,它就是一个函数 f(x),而梯度下降法的目的就是获取这个函数的极小值。
下面给出一个较为正式的问题定义。
假设 f(x)是 R上具有一阶连续偏导数的函数。需要求解的无约束最优化问题是:
即需要求出目标函数 f(x) 的极小点 x∗。
算法思想和推导
要理解梯度下降法,首先要理解梯度和负梯度的概念。
梯度是从 n 维推广出来的概念,类似于斜率。梯度的本意是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
梯度下降法的思想,就是选取适当的初值 x0,不断迭代更新 x 的值,极小化目标函数,最终收敛。
由于负梯度方向是使函数值下降最快的方向,因此梯度下降在每一步采用负梯度方向更新 xx 的值,最终达到函数值最小。
可以看出,梯度下降法采用的是贪心的思想。
一阶泰勒展式
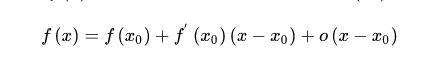
根据一阶泰勒展开,当 x 趋近于 xk 时:
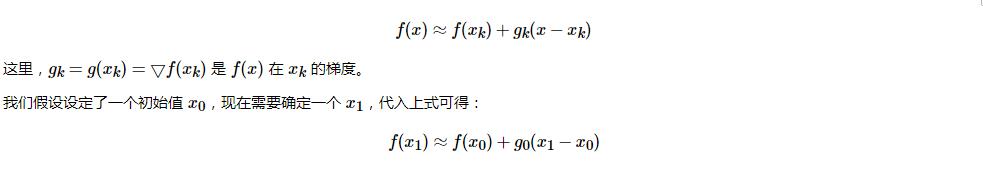
一维问题就是不断求导,直到达到我们设置的精度
其中,学习率 λk 要足够小,使得:
- 满足泰勒公式所需要的精度。
- 能够很好地捕捉到极小值。
这是一个显式表达式,可以不断求出 xk+1xk+1,当满足收敛条件时(如梯度足够小或者 xk+1xk+1 更新变化量足够小),退出迭代,此时 f(xk+1)f(xk+1) 就是一个求解出来的最小函数值。
至此完成了梯度下降法逻辑上的推导。
Python 代码实现
学习率这里 我们是写死的;
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
一维问题的梯度下降法示例
"""
def func_1d(x):
"""
目标函数
:param x: 自变量,标量
:return: 因变量,标量
"""
return x ** 2 + 1
def grad_1d(x):
"""
目标函数的梯度
:param x: 自变量,标量
:return: 因变量,标量
"""
return x * 2
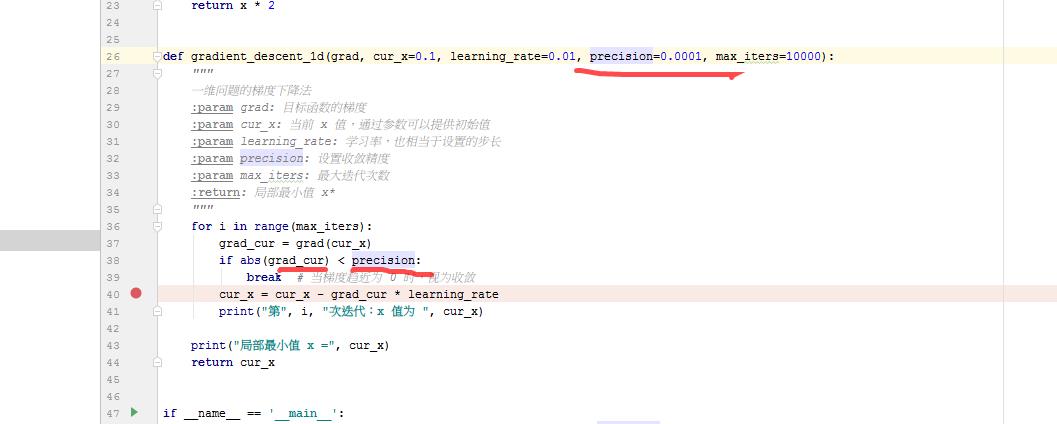
def gradient_descent_1d(grad, cur_x=0.1, learning_rate=0.01, precision=0.0001, max_iters=10000):
"""
一维问题的梯度下降法
:param grad: 目标函数的梯度
:param cur_x: 当前 x 值,通过参数可以提供初始值
:param learning_rate: 学习率,也相当于设置的步长
:param precision: 设置收敛精度
:param max_iters: 最大迭代次数
:return: 局部最小值 x*
"""
for i in range(max_iters):
grad_cur = grad(cur_x)
if abs(grad_cur) < precision:
break # 当梯度趋近为 0 时,视为收敛
cur_x = cur_x - grad_cur * learning_rate
print("第", i, "次迭代:x 值为 ", cur_x)
print("局部最小值 x =", cur_x)
return cur_x
if __name__ == '__main__':
gradient_descent_1d(grad_1d, cur_x=10, learning_rate=0.1, precision=0.01, max_iters=10000)一维问题
假设我们需要求解的目标函数是:最小值在0 点取得
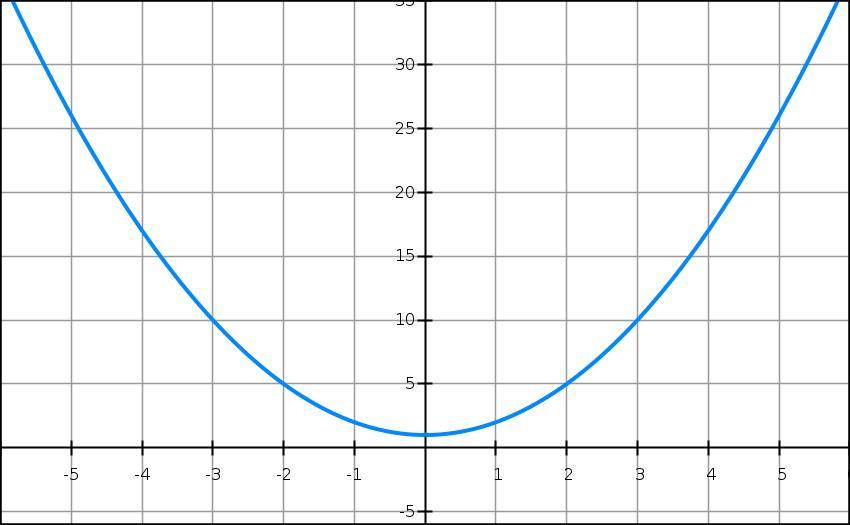
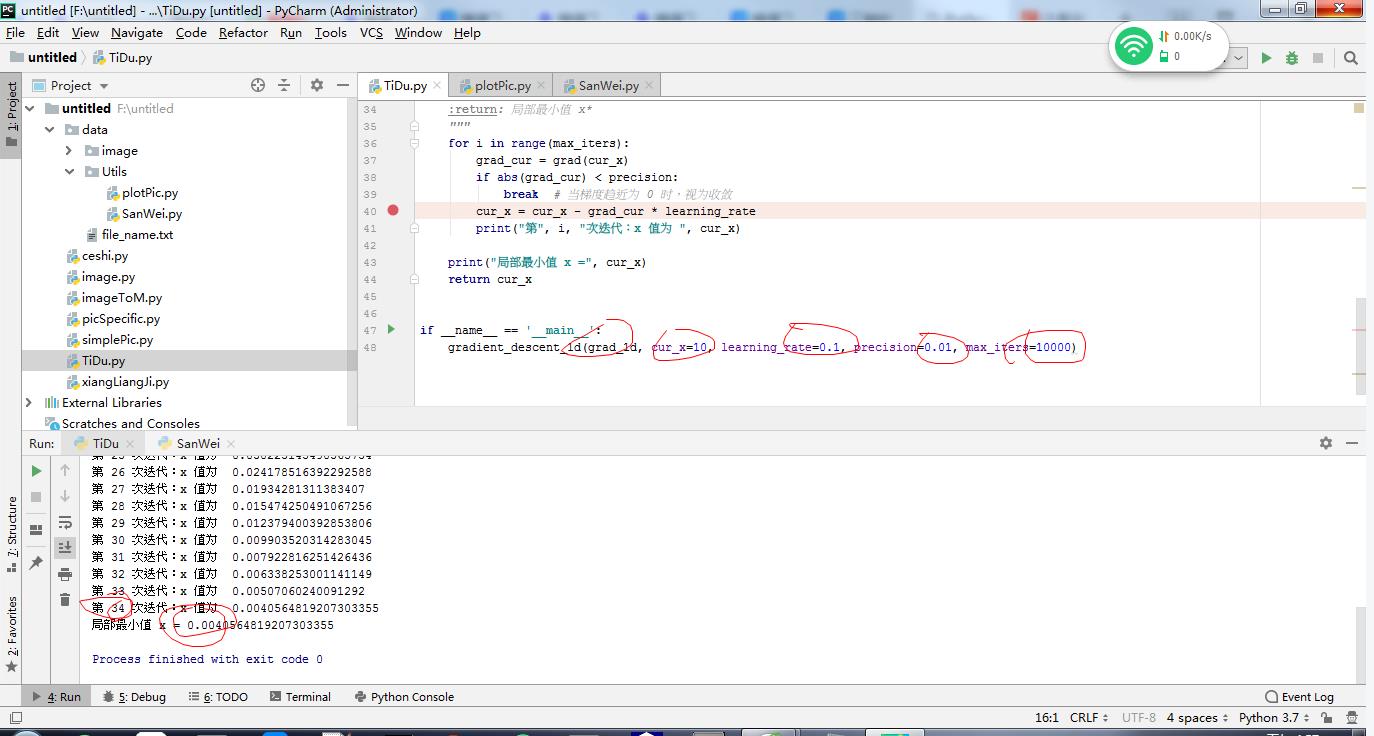
上图就是在倒数小于0.01的时候循环34次求出最小值在近乎0 取得
三维空间梯度下降
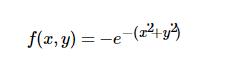 在00 处取得极小值
在00 处取得极小值
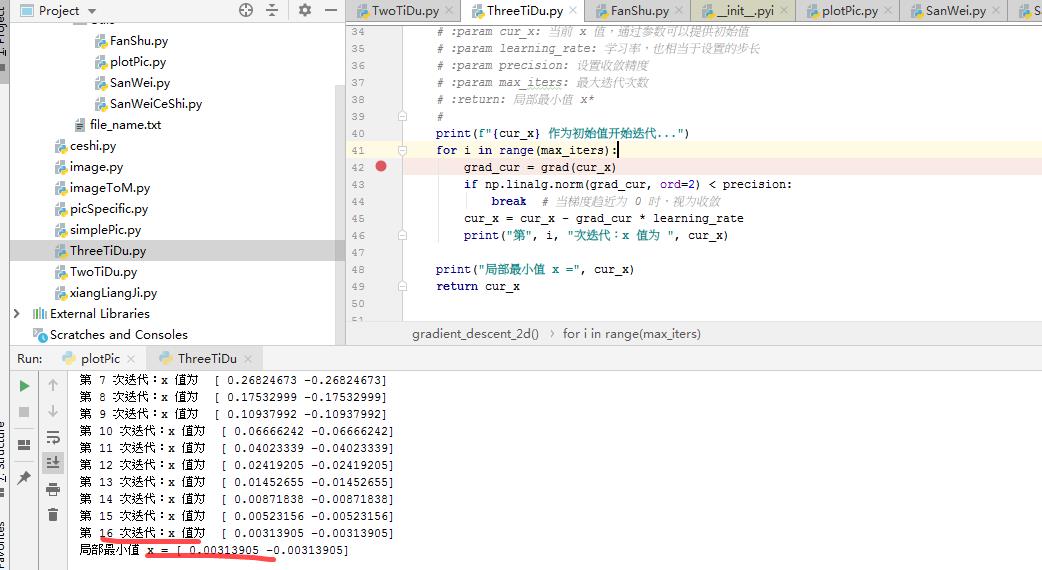
迭代16 次在0 0处取得最小值;
代码展示
其中关键核心代码涉及到范数的问题:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
二维问题的梯度下降法示例
"""
import math
import numpy as np
def func_2d(x):
"""
目标函数
:param x: 自变量,二维向量
:return: 因变量,标量
"""
return - math.exp(-(x[0] ** 2 + x[1] ** 2))
def grad_2d(x):
"""
目标函数的梯度
:param x: 自变量,二维向量
:return: 因变量,二维向量
"""
deriv0 = 2 * x[0] * math.exp(-(x[0] ** 2 + x[1] ** 2))
deriv1 = 2 * x[1] * math.exp(-(x[0] ** 2 + x[1] ** 2))
return np.array([deriv0, deriv1])
def gradient_descent_2d(grad, cur_x=np.array([0.1, 0.1]), learning_rate=0.01, precision=0.0001, max_iters=10000):
#
# 二维问题的梯度下降法
# :param grad: 目标函数的梯度
# :param cur_x: 当前 x 值,通过参数可以提供初始值
# :param learning_rate: 学习率,也相当于设置的步长
# :param precision: 设置收敛精度
# :param max_iters: 最大迭代次数
# :return: 局部最小值 x*
#
print(f"{cur_x} 作为初始值开始迭代...")
for i in range(max_iters):
grad_cur = grad(cur_x)
if np.linalg.norm(grad_cur, ord=2) < precision:
break # 当梯度趋近为 0 时,视为收敛
cur_x = cur_x - grad_cur * learning_rate
print("第", i, "次迭代:x 值为 ", cur_x)
print("局部最小值 x =", cur_x)
return cur_x
if __name__ == '__main__':
gradient_descent_2d(grad_2d, cur_x=np.array([1, -1]), learning_rate=0.2, precision=0.01, max_iters=10000)补充:泰勒展开式的意义
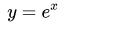
对于一些复杂的函数, 要研究其性质往往是比较困难的. 而多项式函数的性质往往比较简单, 所以有时候, 为了方便研究, 我们可能会想着: 能不能用一个多项式函数去近似一个复杂的函数?
比如说, 现在我们想在点0附近, 用一个多项式函数, 去近似一个复杂函数 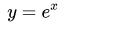 , 那我们应该怎么做呢?
, 那我们应该怎么做呢?
我们知道当x=0时, 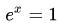 , 所以不妨拿一个"当x=0时, y值也为1的函数"来近似试试, 比如说: y = 1
, 所以不妨拿一个"当x=0时, y值也为1的函数"来近似试试, 比如说: y = 1
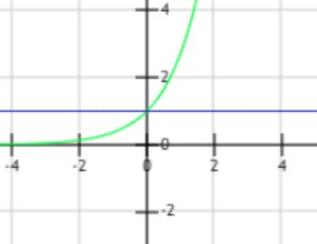
原始函数 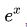 , 近似函数,泰勒一阶展开式在0点的近似函数:y = 1 + x,
, 近似函数,泰勒一阶展开式在0点的近似函数:y = 1 + x,
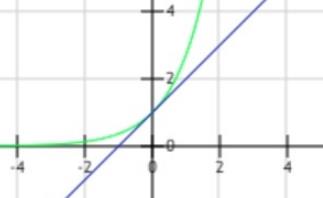
我们尝试在0 点求解二阶泰勒展开式,看看拟合效果

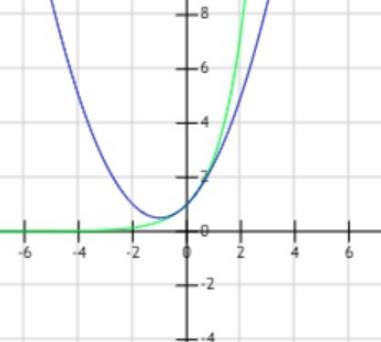
按照这个思路继续求解三阶泰勒展开式
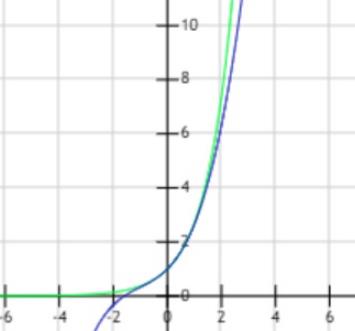
下面不在一一验证,我们可以看到,拟合效果越来越好;
看一下10阶泰勒在0点的展开式
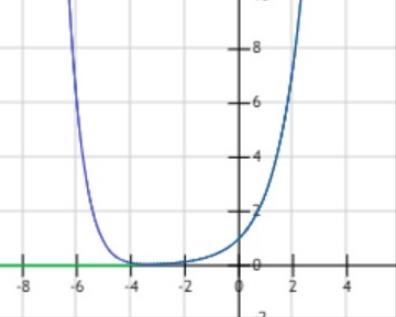
泰勒展示的作用
函数本身我们没有办法计算,但是通过泰勒展开式在某点进行展开,至少在这个区域范围内效果拟合的是较好的,我们有时没有必要知道全部空间 ,仅仅在我们需要计算的空间找一点进行展开即可。
I. 泰勒公式的作用是描述如何在x0点附近, 用一个多项式函数去近似一个复杂函数.
II. 之所以能实现这种近似, 背后的逻辑是:让近似多项式函数在x=x0处的y值, 一阶导, 二阶导 ...n阶导的值 = 原始函数在x=x0处的y值, 一阶导, 二阶导 ...n阶导
即, 如果函数A和函数B在某一点的值一样, 变化率一样, 变化率的变化率一样, 变化率的变化率的变化率也一样... 求导实际就是在拟合函数的变化率
就这样层层深入, 无论深入到哪一个维度, 关于这一点的变化率, 函数A和函数B都是一样的, 那就可以推断:
在这一点上, 函数A和B应该是一样的
在这一点附近, 函数A和B应该很相似
离这一点越远, 函数A和B的相似程度就越难以保证
以上是关于梯度下降法,二维空间三维空间 代码实现的主要内容,如果未能解决你的问题,请参考以下文章