BUAA_2019_数学建模_期末复习提纲

Posted 2020-11-25 fuji-mount

整理者：FUJI_W

时间： 2020年1月2日

考题回顾

建模部分

填空题 - 英文翻译

1. 纳什均衡

2. 博弈论

3. 队列模型

名词解释

**是什么？请举例说明。

1. 纳什均衡

2. 非纳什均衡

简答题

1. 传染病模型 SIS SIR （15分）

2. 存储模型（允许缺货，不允许缺货）（15分）

仿真部分

判断题（10分）

大多是仿真那一节

填空题（10分）

MATLAB的数组赋值，多项式求解；

分布式交互仿真的特点等

简答题（10分）

1. ADAMS（3分）

2. 并行计算树（4分）

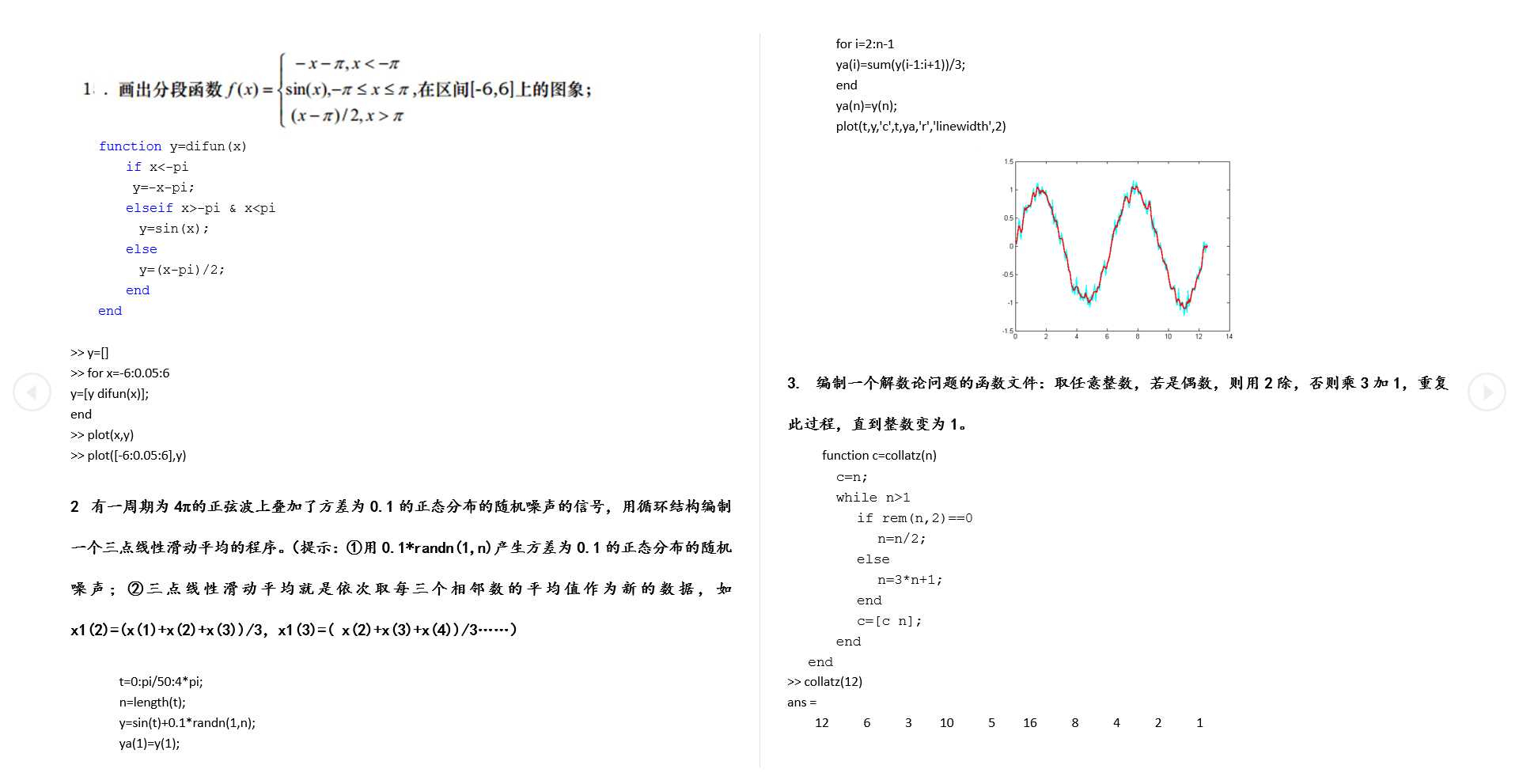
3. MATLAB程序书写（水仙花数的计算）（4分）

---

一、建模

建模基础

1. 实物模型：玩具、照片、飞机、火箭模型；

   物理模型：水箱中的舰艇、风洞中的飞机；

   符号模型：地图、电路图、分子结构图；

2. 数学建模（Mathematical Modeling）：对于一个现实对象 ，为了一个特定目的，根据其内在
   规律，作出必要的简化假设，运用适当的数学工具得到的一个数学结构 。

3. 数学模型（Mathematical）：建立数学模型的全过程。（ 包括表述、求解、解释、检验等 ）

4. 数学建模的基本方法：

   1. 机理分析：主要通过实例研究（Case Studies）来学习。
   2. 测试分析：黑箱测试，通过对量测数据的统计分析，找出与数据拟合最好的模型。
   3. 二者结合：用机理分析建立模型结构，用测试分析确定模型参数。

5. 数学建模一般步骤：

   1.模型求解；2.模型分析；3.模型检验；4.模型应用。

6. 数学模型的分类

   分类标准	具体类别
   对某个实际问题了解的深入程度	白箱模型、灰箱模型、黑箱模型
   模型中变量的特征	连续型模型、离散型模型或确定性模型、随机型模型等
   建模中所用的数学方法	初等模型、微分方程模型、差分方程模型、优化模型等
   研究课题的实际范畴	人口模型、生态系统模型 、交通流模型、经济模型、 基因模型等

模型汇总

1 初等模型

1. 椅子能否在不平的地面上放平

   

2. 赛艇成绩

   

2 数学规划模型

1. 奶制品的生产与销售

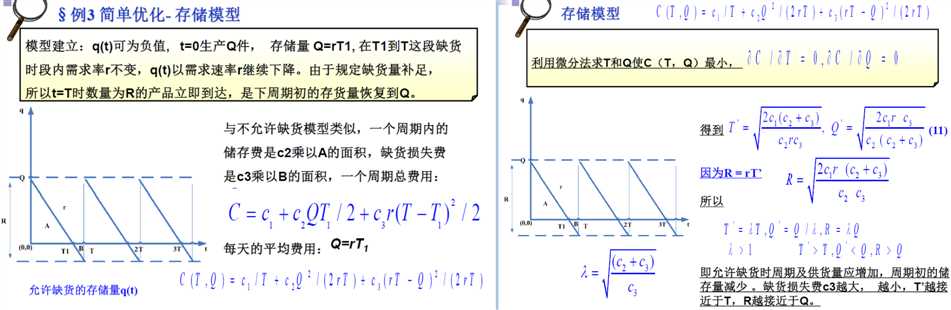
3 简单优化模型

1. 存储模型（允许缺货）

   

2. 存储模型（不允许缺货）

   

4 微分建模

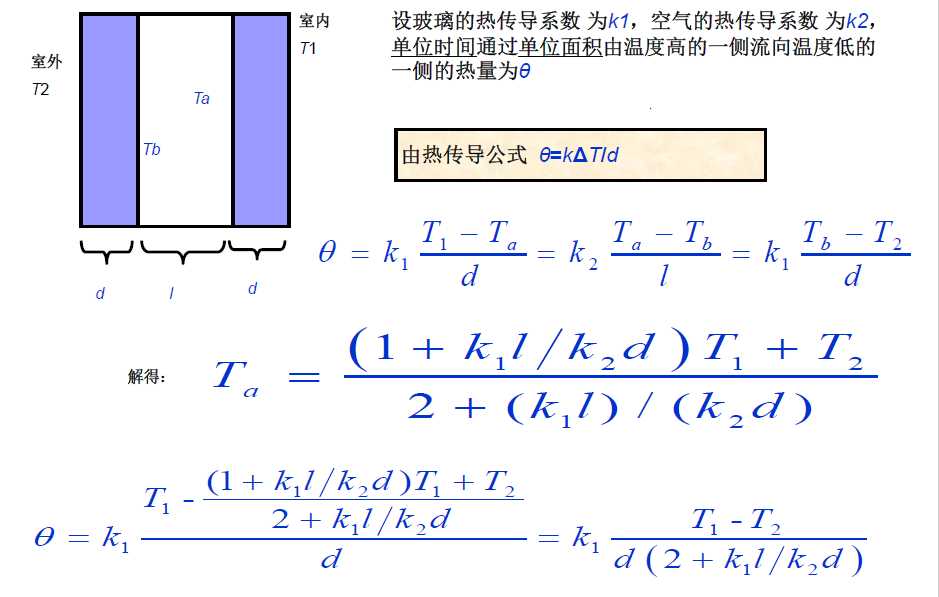
1. 崖高的估计

   

2. 双层玻璃的功效

   

3. ==传染病模型==

   

4. Malthus 人口模型

   

5. Logistic 人口模型

   

6. Lanchester 战争模型

   

7. 多级火箭发射模型

   

8. 军备竞赛模型（稳定性判断方法 p,q>0）

5 差分方程

1. ==市场经济的蛛网模型==

   

6 离散事件仿真

1. 离散事件基本概念

   

2. 仿真时间推进

   1. 固定时间步长推进方法：所有实体的时钟以同样的步长更新；
   2. 下一事件推进方法：时间推进时从当前事件发生时间到下一事件发生时间，也就是说，仿真会跳过没有事件发生的时间段；
   • 未来事件列表（FEL）：包含所有将要调用的事件，并且以时序排列；
   • 执行过程（Executive Routine）：取出下一事件，推进仿真时间并且将控制权交给正确的执行过程。

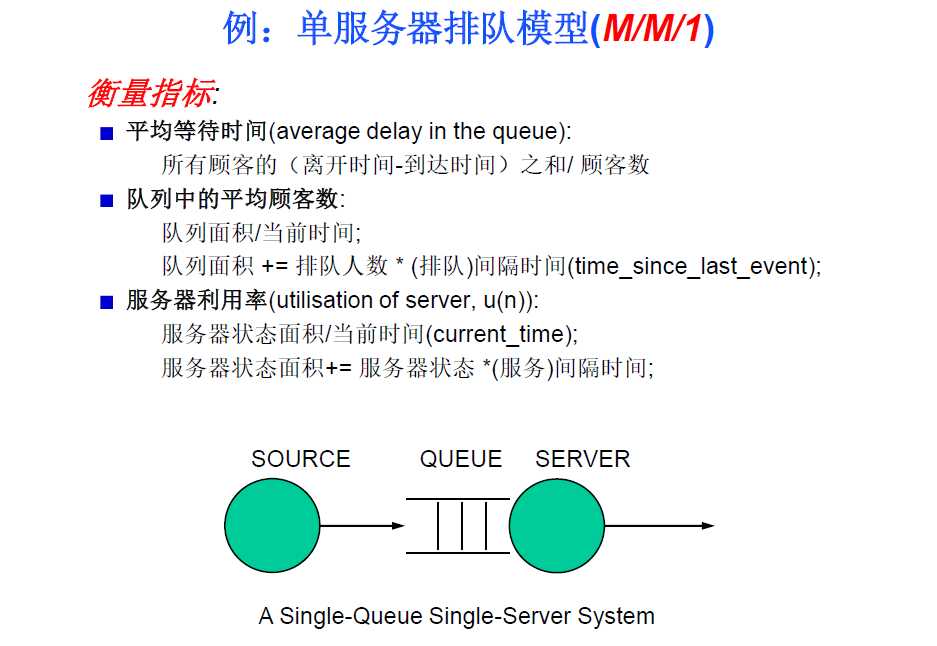
3. 队列模型

   1. M/M/1 中三个参数的意义；

   2. 

7 马氏链模型

1. 概念：描述一类重要的随机动态系统(过程)的模型

   • 系统在每个时期所处的状态是随机的；
   • 从一时期到下时期的状态按一定概率转移；
   • 下时期状态只取决于本时期状态和转移概率. 已知现在，将来与过去无关（无后效性）。

2. 健康与疾病

   

3. 钢琴销售的存储策略

8 离散模型

1. 层次分析法

   • 层次划分：目标层 O，准则层 C，方案层 P；
   • 特点：定性与定量结合；
   • 
   • 

2. 循环比赛的名次

   

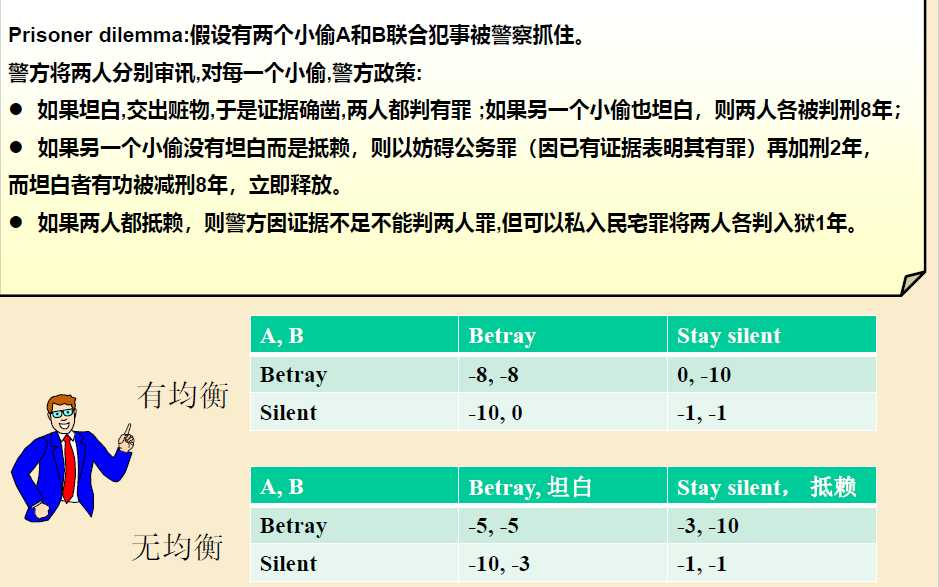
9 博弈模型

1. 多方合作的 Shapley 分配 —— 例 效益的合理分配

   )

2. 纳什均衡（Nash equilibrium）—— 例 进攻与撤退的抉择

   1. 基本概念

      

   2. 实例分析

      

10 社会力模型

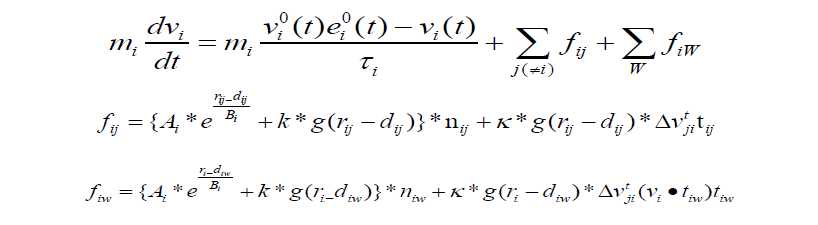
英文汇总

原文	翻译
人口模型	Malthus / Logistic
战争模型	Lanchester
经济订货批量公式	EOQ: Economic Order Quantity
离散事件仿真	Discrete Event Simulation，缩写为 DES 包含 实体（entity）及其相关属性（attribute），活动（activity），事件（event），进程（process），
同步模型	synchronous model of time
异步模型	asynchronous model of time
下一事件时间推进算法	next-event time advance algorithm
层次分析法	Analytic Hierarchy Process
纳什均衡	Nash Equilibrium
支付矩阵	Payoff Matrix
马氏链	Markov Chain

二、仿真

第八章 物理仿真

1 概述

1. 数学仿真

   对实际系统进行抽象，并将其特性用数学关系加以描述而得到系统的数学模型，对数学模型进行实验的过程称为数学仿真。

2. 数字计算机仿真（串行仿真？）

   将系统数学模型用计算机程序加以实现。

3. 物理仿真

   按照真实系统的物理性质构造系统的物理模型，并在物理模型上进行实验的过程称为物理仿真。

4. 半实物仿真

   将数学模型与物理模型甚至实物联合起来进行实验。

   ==当被仿真的系统中存在物理模型或实物时，必须进行实时仿真。物理仿真和半实物仿真均为实时仿真。==

5. 半实物仿真实验（地面物理实验）——飞行控制系统工程

   • 仿：飞行器在空间运动的环境和状态；
   • 真：实际的飞行控制器或主要元部件，如自动驾驶仪、增稳系统、导引头、平台、捷联惯导系统、陀螺等。
   • 组成：仿真计算机，仿真设备，参试设备，实验控制台，支持服务系统。

2 仿真设备及实验原理

? 仿真设备也常被称为模拟器，是半实物仿真中使用数量和种类最多、也最重要一类设备，在系统中用于模拟参试设备所处的真实环境中的某一种物理现象，其模拟或输出的信号是传感器可感知的各种物理现象和效应。

3 仿真器

1. 仿真器是一种有人在回路中的物理仿真系统。
2. 仿真器是一种以计算机为核心的声、光、机电系统。

第九章 并行仿真（重点）

1 一般概念

1. 串行仿真

   • 运算符称为指令流；运算数称为数据流；指令流与数据流合称信息流

   • 一个操作符只对应一组操作数，产生一个计算结果，这种方式称为==单指令流单数据流方式（SISD）==。

     ==以SISD方式工作的计算机是串行计算机，进行的仿真是串行仿真。==

2. 并行处理

   • 同时性：多个事件在同一时刻发生；—— 并行计算
   • 并发性：多个事件在同一时间间隔内发生；—— 串并行混合计算

2 并行计算机的分类及结构

1. 按信息流分类（SIMD，MIMD，MISD）

   

2. 按并行工作单元的层次等级分类

   • 关联并行处理机

     实现存储器操作的并行。

   • 流水线处理机（向量机）

     实现处理器的并行操作。

   • 并行处理机

     实现处理机的并行操作。

   • 多计算机系统

     实现指令和任务的并行。（MIMD）

   • 分布式共享存储多处理机系统（DSM）

     每个并行单元有独立的操作系统。

3 并行算法

1. 计算问题分类

   • 串行计算问题
     若一个问题的计算是按照SISD方式进行，即：每步计算都是一个操作符作用于一组操作数，产生一个结果，当前步计算依赖于前一步的结果，则称为串行计算问题。
   • 并行计算问题
     若一个问题的计算是按照SIMD方式或MIMD方式进行，各分量之间无依赖，则称为并行计算问题。
   • 串并行混合计算问题
     若一个问题既有串行计算部分又有并行计算部分，则称为串并行混合计算问题。

2. 计算机算法的划分

   按指令流与数据流的执行方式

   1. 串行算法：SISD，串行计算机
   2. 同步并行算法：SIMD，并行计算机
   3. 异步并行算法：MIMD，并行计算机

3. ==ADAMS 时序图==

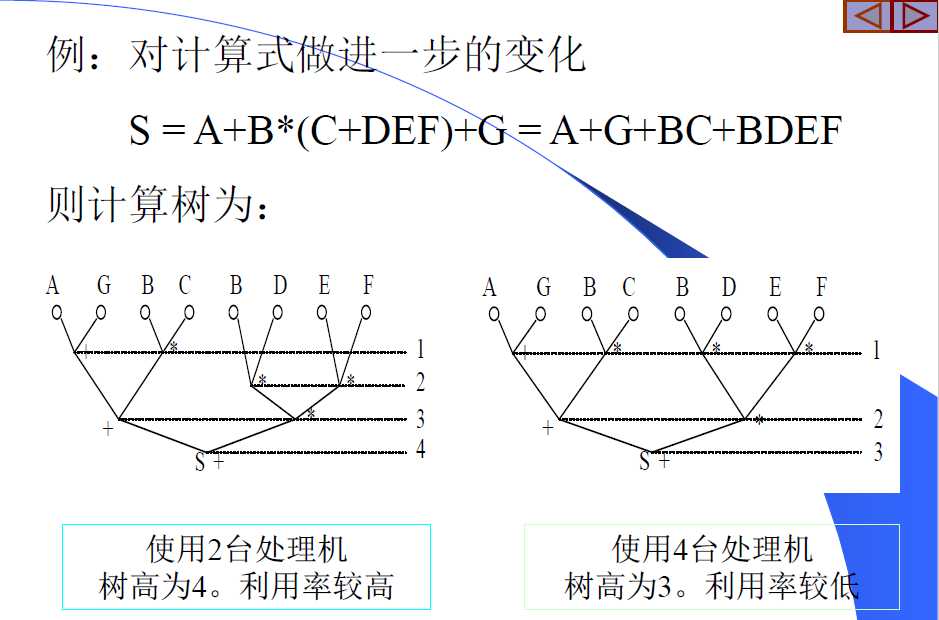
4. ==并行算法的计算树==

   • 名词

     • 树叶：输入的n个数。
     • 节点：双目操作数的操作符。
     • 树枝：节点-节点间或树叶-节点间的连线。
     • 树根：计算结果。
     • 枝高度：树叶到树根间的枝数。
     • 树高：最大枝高度，即计算次数。

   • 

附录