如何在matlab中用样条函数平滑曲线

Posted 2023-05-17

我要对位移曲线求导得到速度曲线，在求导之前想先对位移曲线进行平滑，该用什么方法？用matlab中的spline()可以吗？请说具体些，谢谢了！

也就是用插值方法,增加样点,用样条函数拟合,这样使得曲线平滑了

%不是很平滑的曲线

x=1:5;

y=1+x.^2+8*rand(1,length(x));

plot(x,y,'b-');

%插值,增加x样点数

x1 = 1:0.1:5

%用样条函数插值

y1=spline(x,y,x1);

hold on;

plot(x1,y1,'r-');

(红线比蓝线平滑)

参考技术A 就是用spline()
spline()是根据采集的一些点平滑成一条曲线。
比如：
x=[1 2 3 5 8];
y=[3 2 6 4 9];
t=1:5;
ts=1:0.01:5;
xs=spline(t,x,ts);
ys=spline(t,y,ts);
plot(xs,ys,x,y,'o')

画出的图就是把（x,y) 这5个点进行光滑连接成曲线

matlab练习程序（均匀B样条）

B样条是对贝塞尔曲线的一种扩展，包含两个贝塞尔曲线不具有的优点：

1. B样条的多项式次数可以独立于控制点数目，而贝塞尔曲线次数和控制点是紧密相关的。

2. B样条允许局部控制曲线或曲面生成。

B样条曲线生成的关键是构造出基函数，下面提供了二次、三次和四次三种基函数来进行B样条曲线生成。

matlab代码如下：

clear all;
close all;
clc;

p =ginput();    %至少点五个点，因为下面有四次样条
plot(p(:,1),p(:,2),‘k-o‘);  

%二次均匀b样条
re2=[];
for i=1:length(p)-2  
    for t=0:0.01:1   
        
        b0 = 1/2*(1-t)^2;
        b1 = 1/2*(-2*t^2+2*t+1);
        b2 = 1/2*t^2;
        
        x=b0*p(i,1)+b1*p(i+1,1)+b2*p(i+2,1);
        y=b0*p(i,2)+b1*p(i+1,2)+b2*p(i+2,2);        
        
        re2=[re2;x y];
    end
end

%三次均匀b样条
re3=[];
for i=1:length(p)-3  
    for t=0:0.01:1   
  
        b0=1/6*(1-t)^3;                       
        b1=1/6*(3.*t^3-6*t^2+4);        
        b2=1/6*(-3*t^3+3*t^2+3*t+1);     
        b3=1/6*t^3;                     
  
        x=b0*p(i,1)+b1*p(i+1,1)+b2*p(i+2,1)+b3*p(i+3,1);    
        y=b0*p(i,2)+b1*p(i+1,2)+b2*p(i+2,2)+b3*p(i+3,2);     

        re3=[re3;x y];
    end
end

%四次均匀b样条
re4=[];
for i=1:length(p)-4  
    for t=0:0.01:1   
  
        b0=1/24*(t^4-4*t^3+6*t^2-4*t+1);                     
        b1=1/24*(-4*t^4+12*t^3-6*t^2-12*t+11);      
        b2=1/24*(6*t^4-12*t^3-6*t^2+12*t+11);    
        b3=1/24*(-4*t^4+4*t^3+6*t^2+4*t+1);                     
        b4=1/24*t^4;
        
        x=b0*p(i,1)+b1*p(i+1,1)+b2*p(i+2,1)+b3*p(i+3,1)+b4*p(i+4,1);    
        y=b0*p(i,2)+b1*p(i+1,2)+b2*p(i+2,2)+b3*p(i+3,2)+b4*p(i+4,2);     

        re4=[re4;x y];
    end
end

hold on;  
plot(re2(:,1),re2(:,2),‘r‘);
plot(re3(:,1),re3(:,2),‘g‘);
plot(re4(:,1),re4(:,2),‘b‘);

结果如下：

 

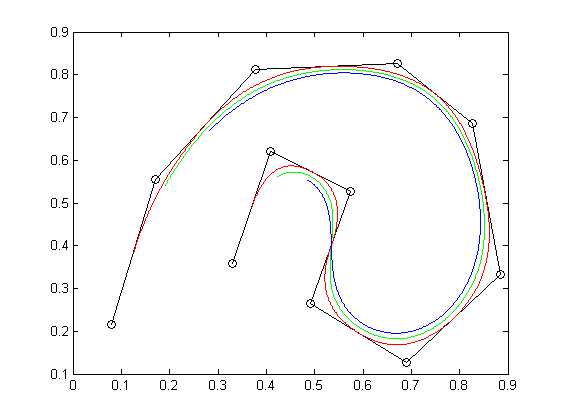
其中黑色为控制点，红色为二次样条，绿色为三次样条，蓝色为四次样条。