通过n+1个控制点求出n段分段函数的解析式

Posted 2020-11-22 dong628

最近刚好学了解析几何，在学完二元一次方程组与一次函数的关系后，我突然有了一个大胆的想法！

可不可以用程序自动求出一次函数的解析式呢？

这个想法源自于最近一段时间数学练习册上百考不厌的同类型题：给定在一次函数图像上的两个点的坐标（互不相同），求出这个一次函数的解析式

 

 

 

 

 

既然是同一类型的题，我又会做，我为什么不让程序帮我做呢？

何况我又是一个拿过PJ省二的OIer（虽然SX很水），而且对自己的数学很有信心。

于是我就在数学课上想这个问题（这就是我上数学课走神的借口？？），并且成功想了出来怎么做。

 

基本思路

众所周知，当我们把一个一次函数用y=kx+b的形式表示时，我们把k叫作斜率，把b叫作截距。

由于一次函数的图像是一条直线，那么可得：当 x1-x2=x2-x3 时，y1-y2=y2-y3，也就是说当自变量x增加的值相等时，因变量y的值增加也相等，这个相信初中数学都已经讲过了；x每增加1，y增加的量就是斜率，这个我相信初中数学也都讲过（虽然教材上没有），而且这个证明过程非常简单。

根据上面两条，不难得出，x每增加n，y增加的值就是n倍的斜率。

所以，要求斜率，可以把两个点的横坐标增加的值m算出来，再算纵坐标增加的值n，然后通过n/m计算出斜率。

至于截距，将随便一个点的x，y，k代入，然后算出b。

用更简单的式子表示，就是：

k=(a-c)/(b-d)

b=b-ak

其中两个点的坐标分别为 ( a, b )，( c, d )

然后数学老师在我想出来10分钟后向我们讲了这个公式

然而，我又看到了这道题：

 

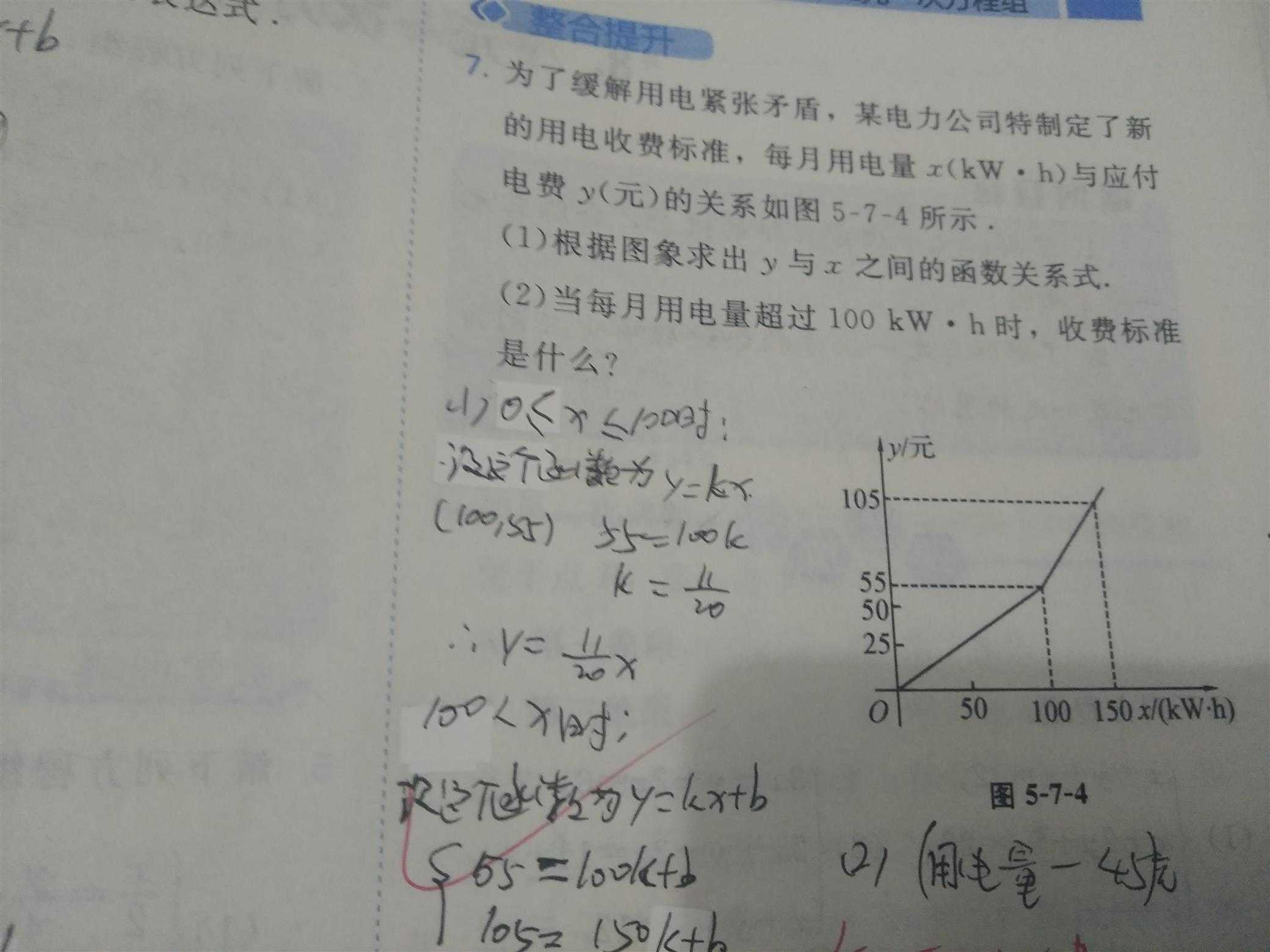
之后又想如何求分段函数。。

这个是比较简单的，把每两个点的函数解析式算出来，然后取值范围就是在两个点的横坐标值之间。

需要注意的是，输入必须是有序的，即从左到右输入，如果不是的话同一个x就可能对应不同的y了。

代码：

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int n;
 5 double point[105][2], k, b;
 6 
 7 int main(){
 8     scanf("%d", &n);
 9     for(int i=0; i<n; i++){
10         scanf("%lf%lf", &point[i][0], &point[i][1]);
11     }
12     for(int i=0; i<n-1; i++){
13         k=(point[i][1]-point[i+1][1])/(point[i][0]-point[i+1][0]);
14         b=point[i][1]-k*point[i][0];
15         printf("y=");
16         if(k==1){
17             printf("x");
18         }
19         else if(k!=0){
20             cout << k << ‘x‘;
21 //            printf("%.2lfx", k);
22         }
23         if(b>0){
24             cout << ‘+‘ << b;
25 //            printf("+%.2lf", b);
26         }
27         else if(b<0){
28             cout << b;
29 //            printf("%.2lf", b);
30         }
31         cout << " (" << point[i][0] << " <= x < " << point[i+1][0] << ")
";
32 //        printf(" (%.2lf <= x < %.2lf)
", point[i][0], point[i+1][0]);
33     }
34 
35     return 0;
36 }

 

这玩意简直是做题神器啊！！