机器学习：PCA（高维数据映射为低维数据 封装&调用）

Posted 2020-11-20 volcao

# 每个主成分向量的长度与数据集的特征数一样

# 主成分分析法的本质：将数据集从一个坐标系转换到另一个坐标系，原坐标系有 n 个维度（n 中特征），则转换的新坐标系也有 n 个维度，每个主成分表示一个维度，只是对于转换后的坐标系，只取前 k 个维度（也就是前 k 个主成分），此 k 个维度相对于数据集更加重要，形成矩阵 W_k ；

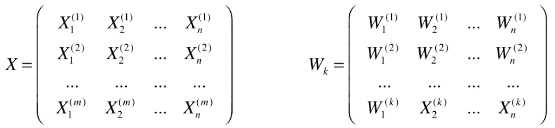
# 将 n 维特征空间转换为 k 维（此为降维的过程）：

　　原则：将 n 维的样本数据转换为 k 维的数据

　　操作：将数据集 X 的一个 n 维样本，与矩阵 W_k 相乘，得到一个 k 维数据；

 

# 将 n 维数据集 X 降维为 k 维数据 X_k：X . W_k^T = X_k ；

 

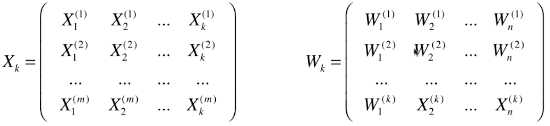
# 将降维后的 k 维数据 X_k 恢复到 n 维数据 X_m ：X_k . W_k = X_m；

　　# 注：恢复后的数据集 X 已经不是原始的数据集了，因为在前期降维的过程回丢失原始数据集的信息，恢复数据集时，丢失的信息无法恢复；

 

# X_m 与原始数据 X 的区别：