matlab 求解一个含参数方程代码

Posted 2023-04-23

我在用Matlab的时候遇上这么一个问题。现在简化一下，问题大概是这样的： 有一个一个函数f(x;a) = x + a，这里，x是自变量，a是一个参数，现在给定一个参数a，要求f(x;a) = 0的值。 我应该怎么编程实现啊？我不需要解析解，要数值解就行了。 我看fsolve的说... 我在用Matlab的时候遇上这么一个问题。现在简化一下，问题大概是这样的： 有一个一个函数f(x;a) = x + a，这里，x是自变量，a是一个参数，现在给定一个参数a，要求f(x;a) = 0的值。 我应该怎么编程实现啊？我不需要解析解，要数值解就行了。 我看fsolve的说明里边，没有传参数的说明啊。 比如说，有这么一段代码： a = 1; x0 = 1; x = fsolve(@f, x0); %现在这样子写不对啊，因为我要传参数a进去，现在没有传进去 %在另一个文件里边： function F = f(x,a) F = x + a; 展开 我还有些问题： 1那种形式不满足我的要求，因为我的那个待求解方程里边还有求和号什么的，一行写不了。 我今天查帮助查到了你说的第4种格式，但是没有太看明白。 x = fsolve(@f, x0,[],a); 第三个参数[]是代表F = f(x,a)里边的第一个参数是自变量吗？比如，我的真正待求解的函数是这样子的： function F = subf(lambda, u, D, beta) %lambda是自变量，其余是参数 所以，我是应该写成下边这个样子吗？ EValues = fsolve(@subf, lambda0, [], u, D, bm); 是这样吗？ 顺便问一下，这个函数有多个根，Matlab支持多个根同时求解吗？或者是我能一次性多给它几个初始试探点x0吗？谢谢！

参考技术A 你的问题属于目标函数存在附加参数情况下怎样传递附加参数的问题，一般有以下几种方法：
1、使用匿名函数，这是最简单的做法：
12345>> a = 1;x0 = 1;>> x = fsolve(@(x)x+a, x0)Optimization terminated: first-order optimality is less than options.TolFun.x = -1
2、使用嵌套函数（Nested
Functions）。
3、使用全局变量（不推荐）。
4、如果优化函数支持附加参数的传递，直接传递，例如，对于你现在的函数，可以直接写成
1x = fsolve(@f, x0,[],a);
对应的匿名函数形式为
1x = fsolve(@(x,a)x+a, x0,[],a)

具体可搜索帮助关于“Passing
Extra
Parameters”的主题。

路径规划基于matlab FMM快速行进法船舶路径规划含Matlab源码 2291期

⛄一、FMM简介

FMM是一种基于熵条件逆风策略求解Eikonal方程的高效数值方法,它在矩形直角格网中求解Eikonal方程的复杂度为O(Nlog N),其中N为格网总数。在一个二维规划空间中,两点之间的最优路径p满足最小代价要求,其中代价C是一个各向异性场,它与位置和方向都有关。
假定有势函数u(x),x表示位置,它满足Eikonal方程:

u(x)按最陡梯度下降的轮廓线就是最优路径,边界条件u(xgoal)=0作为默认已知。当C=1,方程的解就是起点到目标点的欧式距离,它可以简单的通过构造具有单位速度的扩展边界曲线得到。然而,若C不等于1,边界曲线会和自己交叉形成多值的“燕尾解”。熵条件解(没有多值“燕尾”)通常采用粘滞解理论在Eiknoal方程的右边加上平滑项以去除演化边界曲线的“尖角”。添加平滑项后Eiknoal方程形如:

当ε→0时,这种平滑能很好地消除多值“燕尾”现象。FMM是能够自动抽取粘滞解的数值方法,它存在Tsitsiklis算法和Sethian算法两种形式,前者常用于处理可能存在迂回线路的情况,也是本文演化模型FMM实现的基础。

经典的Eiknoal方程一阶求解采用Gudunov逆风策略,该数值方法收敛于粘滞解[7]。在航迹规划中最小代价求解问题的Eiknoal方程通常写成如下形式:

其中T为时间距离函数,τ为扩展代价函数,其Gudunov近似策略为:

通过上述方程和近似计算策略得到时间距离函数分布图,在此基础上利用最陡下降法反向跟踪抽取出发点和目标点之间的最短路径。

⛄二、部分源代码

clc
clear
close all
load mat_T.mat
load map.mat
dbstop if error
tic
% %% 输入起点与终点
% % 起点
% % start = input("请输入起点: ");
% 终点
% goal=input("请输入终点: ");
start=[50,20];
goal=[150,190];

%% 计算速度矩阵V与时间矩阵T
mat_V=ones(size(map));

mat_T=ones(size(map))*inf;
for i=1:size(map,1)
for j=1:size(map,2)
if map(i,j)==0
mat_T(i,j)=NaN;
end
end
end

%初始化mat_T(start)为0
mat_T(goal(1),goal(2))=0;
%初始化Far和Known
Far=[];
Known=[];
for i=1:size(map,1)
for j=1:size(map,2)
if igoal(1)&&jgoal(2)
Known=[i,j];
else
Far=[Far;i,j];
end
end
end

⛄三、运行结果

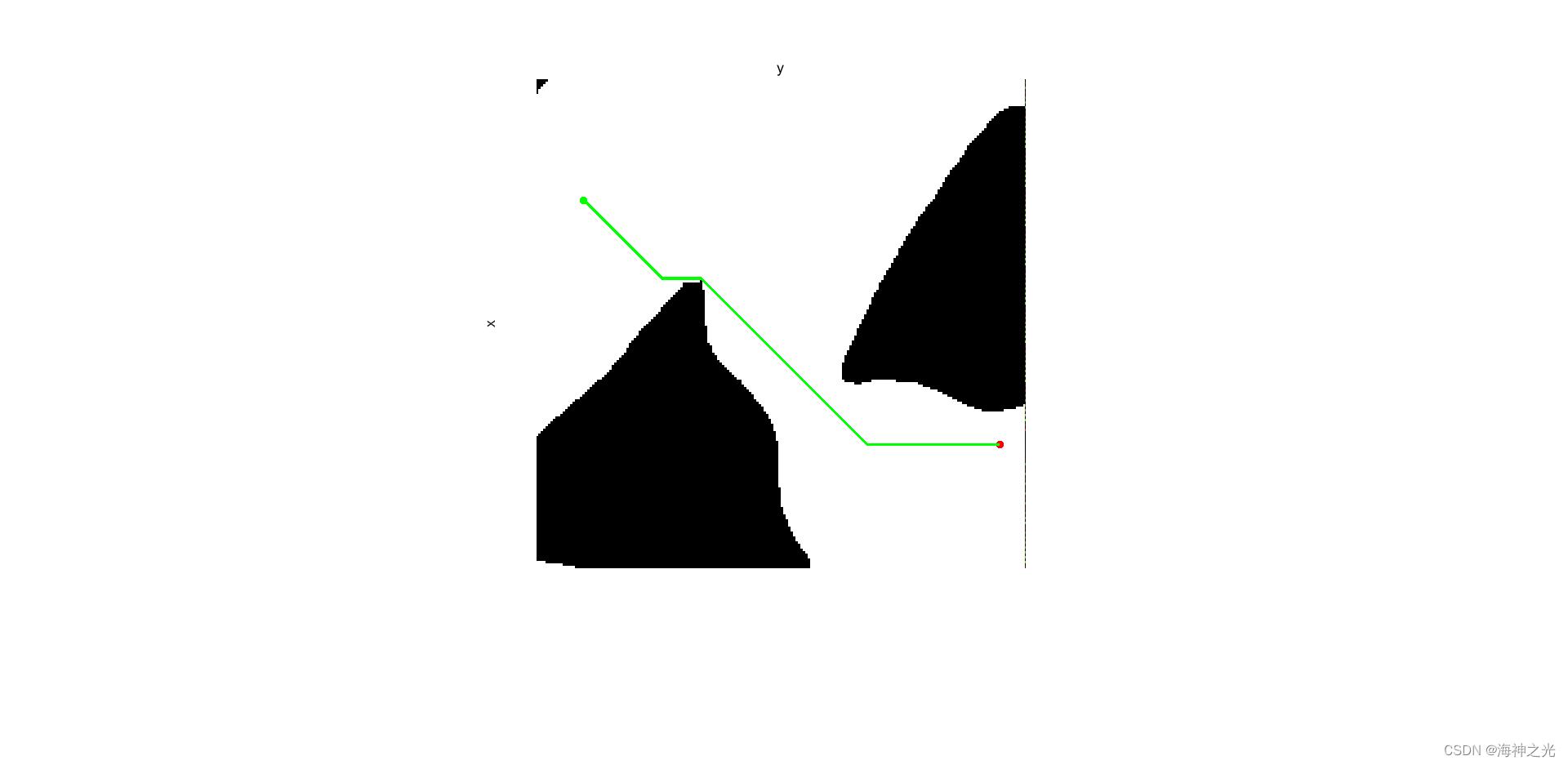
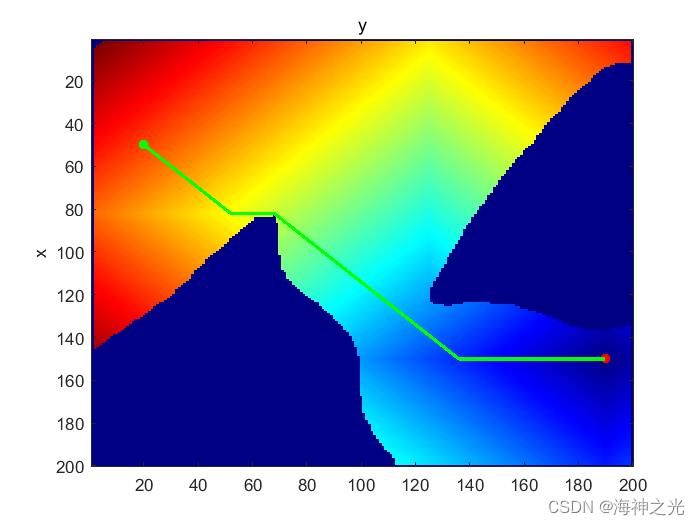
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]李时东,蔡超,丁明跃.一种航迹约束演化新模型及其FMM实现[J].系统仿真学报. 2011,23(05)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除