数据结构(05)_单链表（单链表静态单链表单向循环链表）

Posted 2020-11-19

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构(05)_单链表（单链表静态单链表单向循环链表）相关的知识，希望对你有一定的参考价值。

21.线性表的链式存储结构

21.1.链式存储的定义：

为了表示每个数据元素与其直接后继之间的逻辑关系，数据元素除过存储本身的信息之外，还需要存储其后继元素的地址信息。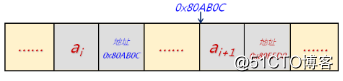
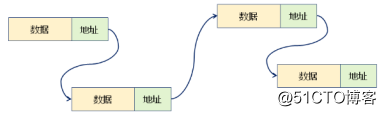
技术分享图片
链式存储结构的逻辑结构：

数据域：存储数据元素本身
指针域：存储相邻节点的地址

统一的专业术语：
— 顺序表：—顺序存储结构的线性表
— 链表：基于链式存储的线性表
单链表：每个节点只包含直接后继的地址信息
循环链表：单链表的最后一个节点的后继为第一个节点
双向链表：节点中包含其直接前驱和后继的信息
链表中基本概念：
— 头节点：链表中的辅助节点，包含指向第一个数据元素的指针，一般不包含数据。
— 数据节点：链表中代表数据元素的节点，表现为：（数据元素、地址）
— 尾节点：链表中最后一个节点，包含的地址信息为空
21.2.单链表

单链表中的节点定义：

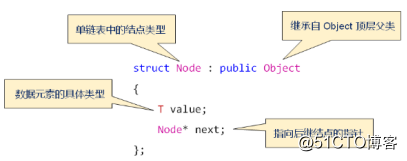
注意：这里的struct是用来定义一个类，与class的访问属性相反，默认为public
单链表的内部结构：
头节点在单链表中的意义是：辅助数据元素的定位，方便插入和删除，因此，头节点不存储实际的数据。

21.3.单链表的插入与删除：

插入：
从头节点开始，通过current指针定位到目标位置
从堆空间中申请新的Node节点
执行插入操作(注意先处理后半部分的挂接，否则会导致链表断开，数据丢失，内存泄漏)
```
node->value = e;
node->next = current->next;
Current->next = node;
```
删除：
从头节点开始，通过current指针定位到目标位置
使用toDel指针指向需要删除的节点
执行操作
```
toDel = current->next;
current->next = toDel->nex;
delete toDel;
```
22.单链表的实现

22.1.设计要点和实现

类族结构：

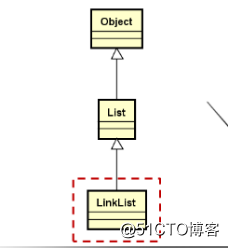
— 类模板，通过头节点访问后继节点
— 定义内部节点的类型Node，用于描述数据域和指针域
— 实现线性表的关键操作，增、删、查等。
```
template < typename T >
class LinkList : public List<T>
{
protected:
struct Node : public Object
{
    Node * next;
    T value;
};
int m_length;
mutable Node m_header;
// 当前所找到的节点不是要直接操作的节点，要操作的是该节点的next
Node *position(int i) const
public:
LinkList()
bool insert(const T& e)
bool insert(int index, const T& e)
bool remove(int index)
bool set(int index, const T& e)
T get(int index)
bool get(int index, T& e) const
int length() const
void clear()
~LinkList()
};
```
22.2.隐患和优化

优化：
代码中多个函数存在对操作节点的定位逻辑。可以将该段代码实现为一个position函数。
```
Node *position(int i) const
{
    Node *ret = reinterpret_cast<Node*>(&m_header);

    for(int p=0; p<i; p++)
    {
        ret = ret->next;
    }

    return ret;
}
```
隐患：

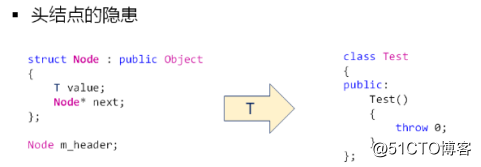
LinkList<Test> L; // 抛出异常，分析为什么我们没有定义 Test 对象，但确抛出了异常
原因在于单链表头节点构造时会调用泛指类型的构造函数
解决方案：
头节点构造时，避免调用泛指类型的构造函数，也即是说要自定义头节点的类型，并且该类型是一个匿名类型
```
mutable struct : public Object
{
    char reserved[sizeof(T)];
    Node *next;
}m_header;
```
注意：这里我们自定义都头结点类型和Node的内存结构上要一模一样（不要将两个成员变量的位置交换）。

22.3 单链表的最终实现

template <typename T>
class LinkList : public List<T>
{
protected:
    int m_length;
    int m_step;

    struct Node : public Object
    {
        Node* next;
        T value;
    };
    // 游标,获取游标指向的数据元素,遍历开始前将游标指向位置为0的数据元素,通过节点中的next指针移动游标
    Node* m_current;

    // 构造头节点时，会调用泛指类型的构造函数，如果泛指类型构造函数中抛出异常，将导致构造失败
    //mutable Node m_header;
    // 为了避免调用泛指类型的构造函数，自定义头节点的类型(内存结构上要一模一样)，并且该类型是一个匿名类型（没有类型名）
    mutable struct : public Object
    {
        Node *next;
        char reserved[sizeof(T)];
    }m_header;

    Node* position(int index) const
    {
        Node* ret = reinterpret_cast<Node*>(&m_header);

        for(int p=0; p<index; p++)
        {
            ret = ret->next;
        }

        return ret;
    }

    virtual Node* create()
    {
        return new Node();
    }

    virtual void destroy(Node* pNode)
    {
        delete pNode;
    }

public:
    LinkList()
    {
        m_header.next = NULL;
        m_length = 0;
        m_step = 0;
        m_current = NULL;
    }

    int find(const T& e) const
    {
        int ret = -1;
        Node* node = m_header.next;

        for(int i=0; i<m_length; i++)
        {
            if(node->value == e)
            {
                ret = i;
                break;
            }

            node = node->next;
        }

        return ret;
    }

    bool insert(const T& e)
    {
        return insert(m_length, e);
    }

    bool insert(int index, const T& e)
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* node = create();
            if(NULL != node)
            {
                Node* current = position(index);

                node->next = current->next;
                current->next = node;
                node->value =e;
                m_length++;
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "no enough memory to insert node.");
            }
        }

        return ret;
    }

    bool remove(int index)
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* current = position(index);

            Node* toDel = current->next;
            if( toDel ==  m_current)
            {
                m_current = toDel->next;    // 确保当前元素删除后m_current指向正确的位置
            }
            current->next = toDel->next;
            destroy(toDel);
            m_length--;
        }

        return ret;
    }

    bool set(int index, const T& e)
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* current = position(index);
            current->next->value = e;
        }

        return ret;
    }

    virtual T get(int index) const
    {
        T ret;

        if(get(index, ret))
        {
            return ret;
        }
        else
        {
            THROW_EXCEPTION(IndexOutOfBoundsException, "index out of range.");
        }
    }

    bool get(int index, T& e) const
    {
        bool ret = (index>=0) && (index<=m_length);

        if(ret)
        {
            Node* current = position(index);
            e = current->next->value;
        }

        return ret;
    }

    void traverse(void)     //O(n^2)
    {
        for(int i=0; i<length(); i++)
        {
            cout << (*this).get(i) << endl;
        }
    }

    void traverse_r(int i, int step = 1)     //O(n)
    {
        for((*this).move(i, step);!(*this).end();(*this).next())    //(*this).move(0,2)
        {
            cout << (*this).current() << endl;
        }
    }

    virtual bool move(int i, int step = 1)    // O(n)
    {
        bool ret = (0<=i)&&(i<m_length)&&(step>0);

        if(ret)
        {
            m_current = position(i)->next;
            m_step = step;
        }

        return ret;
    }

    virtual bool end()
    {
        return (m_current == NULL);
    }

    virtual T current()
    {
        if(!end())
        {
            return m_current->value;
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException,"No value at current position...");
        }
    }

    virtual bool next()
    {
        int i =0;

        while((i<m_step)&&!end())
        {
            m_current = m_current->next;
            i++;
        }

        return(i == m_step);
    }

    int length() const
    {
        return m_length;
    }

    void clear()
    {
        while(m_header.next)
        {
            Node* toDel = m_header.next;
            m_header.next = toDel->next;
            destroy(toDel);
            m_length--;
        }
    }

    ~LinkList()
    {
        clear();
    }

};

23.顺序表和单链表的对比分析

23.1.代码优化

1.查找操作：
可以为线性表list增加一个查找操作， int find (const T& e) const
参数为待查找的元素，返回值为查找到的元素首次出现的位置，没有找到返回 -1
2.比较操作：
当我们定义的了上述查找函数之后，线性表中的数据为类类型时，查找函数编译出错，原因在于我们没有重载==操作符。
解决的办法，在顶层父类Object中重载==和!=操作符，并且让自定义的类继承自顶层父类Object。

23.2.对比分析

单链表和顺序表的时间复杂度对比：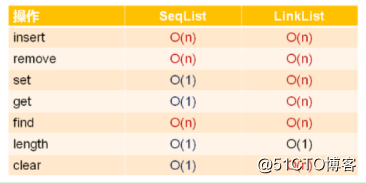
技术分享图片
问题：
顺序表的整体时间复杂度比单链表低，那么单链表还有使用的价值吗？实际工程中为什么单链表反而用的比较多？
——实际工程中，时间复杂度只是效率的一个参考指标

对于内置基础类型，顺序表和单链表的效率不相上下（或者说顺序表更优）
对于自定义类型，顺序表在效率上低于单链表
效率的深度分析：
插入和删除
——顺序表：涉及大量数据对象的复制操作
——单链表只涉及指针操作，效率与对象无关
数据访问
——顺序表：随机访问，可以直接定位数据对象
——单链表：顺序访问，必须从头开始访问数据无法直接定位
工程开发中的选择:
顺序表
——数据元素的类型相对简单，不涉及深拷贝
——数据元素相对稳定，访问操作远远多于插入和删除
单链表：
——数据元素相对复杂，复制操作相对耗时
——数据元素不稳定，需要经常插入和删除，访问操作较少
总结：
线性表中元素的查找依赖于相等比较操作符（==）
顺序表适用于访问需求较大的场合（随机访问）
单链表适用于数据元素频繁插入删除的场合（顺序访问）
当数据元素类型相对简单时，两者效率不相上下
24.单链表的遍历与优化

24.1.遍历

遍历一个单链表的方法：通过for循环来调用get函数即可实现。
```
for(int i=0; i<list.length(); i++)
{
cout << list.get(i) << endl;
}
```
这段代码的时间复杂度为O（n^2）,所以我们希望对其优化，得到一个线性阶的遍历函数。

24.2.设计思路：
在单链表的内部定义一个游标（Node *m_current）
遍历开始前将游标指向位置为0的数据元素
获取游标指向的数据元素
通过节点中的next指针移动游标
提供一组遍历相关的函数，以线性的时间复杂度遍历链表

函数原型：
```
bool move(int i, int step = 1);
bool end();
T current();
bool next();
```
24.3.优化

单链表内部的一次封装：
```
virtual Node *create()
{
    return new Node();
}
virtual void destory(Node *pn)
{
    delete pn;
}
```
进行上述封装得到意义：增加程序的可扩展性

25.静态单链表的实现

25.1.单链表的缺陷：

长时间使用单链表对象频繁的增加和删除数据元素，会导致堆空间产生大量的内存碎片，导致系统运行缓慢。
新的线性表：
在单链表的内部增加一片预留的空间，所有的node对象都在这篇空间中动态创建和动态销毁。

层次结构：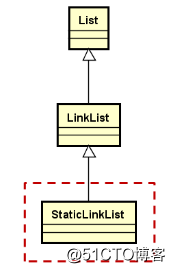

25.2.设计思路：
类模板，继承自LinkList
在类中定义固定大小的空间（unsigned char[N]）
重写create和destroy函，改变内存的分配和归还方式
在Node类中重载operator new，用于指定在内存上创建对象

template < typename T, int N>
class StaticLinkList : public LinkList<T>
{
protected:
    // (1)注意这里不能直接写为Node，编译报错，原因是Node中涉及泛指类型T，所以要声明 LinkList<T>::Node
    // (2)上面的写法在某些编译情况下依然会报错，原因在于，编译器不知道这里的Node是一个类对象，还是一个静态成员对象，
    //    所以前面还需使用template声明Node是一个类对象。
    typedef typename LinkList<T>::Node Node;
    struct SNode : public Node
    {
      void *operator new (unsigned int size, void *p)
      {
          (void)size;
          return p;
      }
    };

    unsigned char m_space[sizeof(SNode) *N];
unsigned int m_used[N];

   Node *create()
   {
        SNode *ret = NULL;

        for(int i=0; i<N; i++)
        {
            if( !m_used[i] )     // 0为空，1为有数据元素，不可用
            {
                ret = reinterpret_cast<SNode*>(m_space) + i;
                ret = new(ret)SNode;    //返回指定内存地址
                m_used[i] = 1;
                break;
            }
        }
        return ret;
   }

   void destroy(Node *pn)
   {
        SNode *space = reinterpret_cast<SNode *>(m_space);
        SNode *spn = dynamic_cast<SNode*>(pn);

        for(int i=0; i<N; i++)
        {
            if( pn == (space + i) )
            {
                m_used[i] = 0;
                spn->~SNode();      //直接调用析构函数
            }
        }
   }

public:
    StaticLinkList()
    {
        for(int i=0; i<N; i++)
        {
            m_used[i] = 0;
        }
    }

};

上节封装create和destroy的意义：
为了本节实现StaticList 做准备，两者的不同之处在于链表节点内存分配的不同，因此将仅有的不同封装与父类和子类的虚函数中。最终通过多态技术，来实现。

25.3 静态单链表的最终实现

template <typename T, int N>
class StaticLinkList : public LinkList<T>
{
protected:
    // typename 表明Node是一个类而非静态成员变量，Node中包含泛指类型，所以使用 LinkList<T>指明
    typedef typename LinkList<T>::Node Node;
    struct SNode : public Node
    {
        // 重载后的结果，返回指定内存空间
        void* operator new(unsigned int size, void* p)
        {
            (void)size;
            return p;
        }
    };

    unsigned int m_space[N];
    unsigned int m_used[N];

    Node* create(void)
    {
        SNode* ret = NULL;

        for(int i=0; i<N; i++)
        {
            if(!m_used[i])
            {
                ret = reinterpret_cast<SNode*>(m_space) + i;
                ret = new(ret) SNode();     //返回指定内存空间
                break;
            }
        }
        return ret;
    }

    void destroy(Node* pn)
    {
        SNode* space = reinterpret_cast<SNode*>(m_space);
        SNode* spn = dynamic_cast<SNode*>(pn);

        for(int i=0; i<N; i++)
        {
            if(pn == space+i)
            {
                m_used[i] = 0;
                spn->~SNode();
                break;
            }
        }
    }

public:
    StaticLinkList()
    {
        for(int i=0; i<N; i++)
        {
            m_used[i] = 0;
        }
    }

    int capacity(void)
    {
        return N;
    }

/**
析构函数定义的原则：对于一个独立类，构造函数中没有使用系统资源，则可以不用定义析构函数，使用系统默认系统的即可。
但对于StaticLinkList这个类，继承制LinkList，当我们没有定义该类的析构函数时：在对象析构时，会默认去调用编译器自己提供的析构函数，然后再调用其父类的析构函数，再其父类的析构函数中会调用clear函数，最终会调用父类的destroy函数。
在父类的destroy 中会使用delete去释放堆空间，而我我们StaticLinkList中的数据并不是在堆空间的，所以会导致程序的不稳定。
解决办法：自定义析构函数，最终调用子类的destroy函数。
**/
    ~StaticLinkList()
    {
        this->clear();
    }

};

29.循环链表

29.1.概念和结构

1.什么是循环链表？
概念上：任意元素有一个前驱和后继，所有数据元素的关系构成一个环
实现上：循环链表是一种特殊的链表，尾节点的指针保存了首节点的地址。
逻辑构成：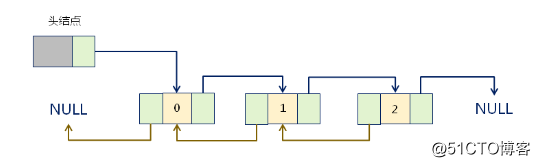
技术分享图片

29.2.继承关系和实现要点

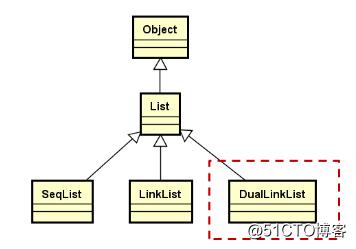
技术分享图片
实现思路：
1.通过模板定义CircleList类，继承自LinkList类
2.定义内部函数last_to_first()用于将单链表首尾相连
3.特殊处理：
首元素的插入和删除操作：
插入首元素时，先将头结点和尾节点的指针指向要插入的元素，然后将要插入元素的指针指向之前的首节点；
删除首节点时，首先将尾节点和头的指针指向要删除节点的下个节点）。
4.重新实现：清空操作和遍历操作，注意异常安全（注意异常安全）。
循环链表可用于解决约瑟夫环的问题。
循环链表声明：

template < typename T >
class CircleList : public LinkList<T>
{
protected:
    Node* last() const
    void last_to_first() const
    int mod(int i) const
public:
    bool insert(const T& e)
    bool insert(int index, const T& e)
    bool remove(int index)
    bool set(int index, const T& e)
    bool get(int index, const T& e) const
    T get(int index) const
    int find (const T& e) const
    void clear()
    bool move(int i, int step)
    bool end()
    ~CircleList()
};

注意：循环链表的实现中，查找和遍历及清空操作要注意异常安全。不能改变链表的状态（比如先将循环链表改为单链表，然后直接调用单链表的相关实现，最后再将链表首尾相连。这样操作如果再过程中调用了泛指类型的构造函数，而且抛出异常，将导致循环链表变成单链表）。

29.3 循环链表的最终实现

template < typename T >
class CircleLinkList : public LinkList<T>
{
protected:
    typedef typename LinkList<T>::Node Node;
    int mod(int i)
    {
        return ( (this->m_length == 0) ? 0 : (i % this->m_length));
    }

    Node* last()
    {
        return this->position(this->m_length-1)->next;
    }

    void last_to_first()
    {
        last()->next = this->m_header.next;
    }

public:
    bool insert(const T& e)
    {
        return insert(this->m_length, e);
    }

    bool insert(int index, const T& e)
    {
        bool ret = true;
        index = index % (this->m_length + 1);   // 可插入点=length+1

        ret = LinkList<T>::insert(index, e);

        if(index == 0)
        {
            last_to_first();
        }

        return ret;
    }

    bool remove(int index)
    {
        bool ret = true;
        index = mod(index);

        if(index == 0)
        {
            Node* toDel = this->m_header.next;

            if(toDel != NULL)   // 类似于判断index是否合法
            {
                this->m_header.next = toDel->next;
                this->m_length--;

                if(this->m_length > 0)
                {
                    last_to_first();
                    if(this->m_current == toDel)
                    {
                        this->m_current = toDel->next;
                    }
                }
                else
                {
                    this->m_current = NULL;
                    this->m_header.next = NULL;
                    this->m_length = 0;
                }
            }
            else
            {
                ret = false;
            }
        }
        else
        {
            ret = LinkList<T>::remove(index);
        }

        return ret;
    }

    T get(int index)
    {
        return LinkList<T>::get(mod(index));
    }

    bool get(int index, T& e)
    {
        return LinkList<T>::get(mod(index), e);
    }

    bool set(int index, const T& e)
    {
        return LinkList<T>::set(mod(index), e);
    }

    int find(const T& e) const
    {
        int ret = -1;
        Node* node = this->m_header.next;

        for(int i=0; i<this->m_length; i++)
        {
            if(node->value == e)
            {
                ret = i;
                break;
            }

            node = node->next;
        }

        return ret;
    }

    bool move(int i, int step)
    {
        return LinkList<T>::move(mod(i), step);
    }

    bool end()
    {
        return ( (this->m_current == NULL) || (this->m_length == 0) );
    }

    void clear()
    {
        if(this->m_length > 1)
        {
            remove(1);
        }
        if(this->m_length == 1)
        {
            Node* toDel = this->m_header.next;

            this->m_current = NULL;
            this->m_header.next = NULL;
            this->m_length = 0;

            this->destroy(toDel);
        }
    }

    ~CircleLinkList()
    {
        clear();
    }
};

以上是关于数据结构(05)_单链表（单链表静态单链表单向循环链表）的主要内容，如果未能解决你的问题，请参考以下文章

循环链表（循环单链表循环双链表）的相关操作的代码实现（C语言）

数据结构学习笔记（单链表单循环链表带头双向循环链表）的增删查改排序等）

第二十五课静态单链表的实现

数据结构开发：静态单链表的实现

循环单链表实现

数据结构(05)_单链表（单链表静态单链表单向循环链表）

21.线性表的链式存储结构

21.1.链式存储的定义：

21.2.单链表

21.3.单链表的插入与删除：

22.单链表的实现

22.1.设计要点和实现

22.2.隐患和优化

22.3 单链表的最终实现

23.顺序表和单链表的对比分析

23.1.代码优化

23.2.对比分析

24.单链表的遍历与优化

24.1.遍历

24.2.设计思路：

24.3.优化

25.静态单链表的实现

25.1.单链表的缺陷：

25.2.设计思路：

25.3 静态单链表的最终实现

29.循环链表

29.1.概念和结构

29.2.继承关系和实现要点

29.3 循环链表的最终实现