数据结构开发:静态单链表的实现
Posted pylearn
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构开发:静态单链表的实现相关的知识,希望对你有一定的参考价值。
0.目录
1.单链表的遍历与优化
2.静态单链表的实现
3.小结
1.单链表的遍历与优化
问题:
- 如何遍历单链表中的每一个数据元素?
当前单链表的遍历方法:

遗憾的事实:
- 不能以线性的时间复杂度完成单链表的遍历
新的需求:
- 为单链表提供新的方法,在线性时间内完成遍历
设计思路 ( 游标 ):
- 在单链表的内部定义一个游标( Node* m_current )
- 遍历开始前将游标指向位置为0的数据元素
- 获取游标指向的数据元素
- 通过结点中的next指针移动游标
提供一组遍历相关的函数,以线性的时间复杂度遍历链表。

遍历函数原型设计:
bool move(int i, int step = 1);bool end();T current();bool next();
单链表的遍历:
改进LinkList.h
#ifndef LINKLIST_H
#define LINKLIST_H
#include "List.h"
#include "Exception.h"
namespace StLib
{
template <typename T>
class LinkList : public List<T>
{
protected:
struct Node : public Object
{
T value;
Node* next;
};
mutable struct : public Object
{
char reserved[sizeof(T)];
Node* next;
} m_header;
int m_length;
int m_step;
Node* m_current;
Node* position(int i) const
{
Node* ret = reinterpret_cast<Node*>(&m_header);
for(int p=0; p<i; p++)
{
ret = ret->next;
}
return ret;
}
public:
LinkList()
{
m_header.next = NULL;
m_length = 0;
m_step = 1;
m_current = NULL;
}
bool insert(const T& e)
{
return insert(m_length, e);
}
bool insert(int i, const T& e)
{
bool ret = ((0 <= i) && (i <= m_length));
if( ret )
{
Node* node = new Node();
if( node != NULL )
{
Node* current = position(i);
node->value = e;
node->next = current->next;
current->next = node;
m_length++;
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to insert new element ...");
}
}
return ret;
}
bool remove(int i)
{
bool ret = ((0 <= i) && (i < m_length));
if( ret )
{
Node* current = position(i);
Node* toDel = current->next;
current->next = toDel->next;
delete toDel;
m_length--;
}
return ret;
}
bool set(int i, const T& e)
{
bool ret = ((0 <= i) && (i < m_length));
if( ret )
{
position(i)->next->value = e;
}
return ret;
}
T get(int i) const
{
T ret;
if( get(i, ret) )
{
return ret;
}
else
{
THROW_EXCEPTION(IndexOutOfBoundsException, "Invalid parameter i to get element ...");
}
return ret;
}
bool get(int i, T& e) const
{
bool ret = ((0 <= i) && (i < m_length));
if( ret )
{
e = position(i)->next->value;
}
return ret;
}
int find(const T& e) const
{
int ret = -1;
int i = 0;
Node* node = m_header.next;
while ( node )
{
if( node->value == e )
{
ret = i;
break;
}
else
{
node = node->next;
i++;
}
}
return ret;
}
int length() const
{
return m_length;
}
void clear()
{
while ( m_header.next )
{
Node* toDel = m_header.next;
m_header.next = toDel->next;
delete toDel;
}
m_length = 0;
}
bool move(int i, int step = 1)
{
bool ret = (0 <= i) && (i < m_length) && (step > 0);
if( ret )
{
m_current = position(i)->next;
m_step = step;
}
return ret;
}
bool end()
{
return (m_current == NULL);
}
T current()
{
if( !end() )
{
return m_current->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
}
}
bool next()
{
int i = 0;
while( (i < m_step) && !end() )
{
m_current = m_current->next;
i++;
}
return (i == m_step);
}
~LinkList()
{
clear();
}
};
}
#endif // LINKLIST_Hmain.cpp测试
#include <iostream>
#include "LinkList.h"
using namespace std;
using namespace StLib;
int main()
{
LinkList<int> list;
for(int i=0; i<5; i++)
{
list.insert(0, i);
}
for(list.move(0); !list.end(); list.next())
{
cout << list.current() << endl;
}
return 0;
}运行结果为:
4
3
2
1
0单链表内部的一次封装:

内部的封装:
改进LinkList.h
#ifndef LINKLIST_H
#define LINKLIST_H
#include "List.h"
#include "Exception.h"
namespace StLib
{
template <typename T>
class LinkList : public List<T>
{
protected:
struct Node : public Object
{
T value;
Node* next;
};
mutable struct : public Object
{
char reserved[sizeof(T)];
Node* next;
} m_header;
int m_length;
int m_step;
Node* m_current;
Node* position(int i) const
{
Node* ret = reinterpret_cast<Node*>(&m_header);
for(int p=0; p<i; p++)
{
ret = ret->next;
}
return ret;
}
virtual Node* create()
{
return new Node();
}
virtual void destroy(Node* pn)
{
delete pn;
}
public:
LinkList()
{
m_header.next = NULL;
m_length = 0;
m_step = 1;
m_current = NULL;
}
bool insert(const T& e)
{
return insert(m_length, e);
}
bool insert(int i, const T& e)
{
bool ret = ((0 <= i) && (i <= m_length));
if( ret )
{
Node* node = create();
if( node != NULL )
{
Node* current = position(i);
node->value = e;
node->next = current->next;
current->next = node;
m_length++;
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to insert new element ...");
}
}
return ret;
}
bool remove(int i)
{
bool ret = ((0 <= i) && (i < m_length));
if( ret )
{
Node* current = position(i);
Node* toDel = current->next;
current->next = toDel->next;
destroy(toDel);
m_length--;
}
return ret;
}
bool set(int i, const T& e)
{
bool ret = ((0 <= i) && (i < m_length));
if( ret )
{
position(i)->next->value = e;
}
return ret;
}
T get(int i) const
{
T ret;
if( get(i, ret) )
{
return ret;
}
else
{
THROW_EXCEPTION(IndexOutOfBoundsException, "Invalid parameter i to get element ...");
}
return ret;
}
bool get(int i, T& e) const
{
bool ret = ((0 <= i) && (i < m_length));
if( ret )
{
e = position(i)->next->value;
}
return ret;
}
int find(const T& e) const
{
int ret = -1;
int i = 0;
Node* node = m_header.next;
while ( node )
{
if( node->value == e )
{
ret = i;
break;
}
else
{
node = node->next;
i++;
}
}
return ret;
}
int length() const
{
return m_length;
}
void clear()
{
while ( m_header.next )
{
Node* toDel = m_header.next;
m_header.next = toDel->next;
destroy(toDel);
}
m_length = 0;
}
bool move(int i, int step = 1)
{
bool ret = (0 <= i) && (i < m_length) && (step > 0);
if( ret )
{
m_current = position(i)->next;
m_step = step;
}
return ret;
}
bool end()
{
return (m_current == NULL);
}
T current()
{
if( !end() )
{
return m_current->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
}
}
bool next()
{
int i = 0;
while( (i < m_step) && !end() )
{
m_current = m_current->next;
i++;
}
return (i == m_step);
}
~LinkList()
{
clear();
}
};
}
#endif // LINKLIST_H问题:
- 封装 create 和 destroy 函数的意义是什么?
2.静态单链表的实现
单链表的一个缺陷:
- 触发条件
- 长时间使用单链表对象频繁增加和删除数据元素
- 可能的结果
- 堆空间产生大量的内存碎片,导致系统运行缓慢
新的线性表
- 设计思路:
- 在“单链表”的内部增加一片预留的空间,所有的Node对象都在这片空间中动态创建和动态销毁。

静态单链表的继承层次结构:
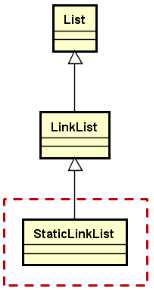
静态单链表的实现思路:
- 通过模板定义静态单链表类( StaticLinkList )
- 在类中定义固定大小的空间( unsigned char[] )
- 重写 create 和 destroy 函数,改变内存的分配和归还方式
- 在Node类中重载 operator new,用于在指定内存上创建对象
(在StLib中实现StaticLinkList.h):
#ifndef STATICLINKLIST_H
#define STATICLINKLIST_H
#include "LinkList.h"
namespace StLib
{
template <typename T, int N>
class StaticLinkList : public LinkList<T>
{
protected:
typedef typename LinkList<T>::Node Node;
struct SNode : public Node
{
void* operator new(size_t size, void* loc)
{
(void)size;
return loc;
}
};
unsigned char m_space[sizeof(SNode) * N];
int m_used[N];
Node* create()
{
SNode* ret = NULL;
for(int i=0; i<N; i++)
{
if( !m_used[i] )
{
ret = reinterpret_cast<SNode*>(m_space) + i;
ret = new(ret)SNode();
m_used[i] = 1;
break;
}
}
return ret;
}
void destroy(Node *pn)
{
SNode* space = reinterpret_cast<SNode*>(m_space);
SNode* psn = dynamic_cast<SNode*>(pn);
for(int i=0; i<N; i++)
{
if( psn == (space + i) )
{
m_used[i] = 0;
psn->~SNode();
}
}
}
public:
StaticLinkList()
{
for(int i=0; i<N; i++)
{
m_used[i] = 0;
}
}
int capacity()
{
return N;
}
};
}
#endif // STATICLINKLIST_Hmain.cpp测试
#include <iostream>
#include "StaticLinkList.h"
using namespace std;
using namespace StLib;
int main()
{
StaticLinkList<int, 5> list;
for(int i=0; i<5; i++)
{
list.insert(0, i);
}
for(list.move(0); !list.end(); list.next())
{
cout << list.current() << endl;
}
return 0;
}运行结果为:
4
3
2
1
0Q & A:
- LinkList 中封装 create 和 destroy 函数的意义是什么?
- 为静态单链表( StaticLinkList )的实现做准备。StaticLinkList 与 LinkList 的不同仅在于链表结点内存分配上的不同;因此,将仅有的不同封装于父类和子类的虚函数中。
3.小结
- 单链表的遍历需要在线性时间内完成
- 在单链表内部定义游标变量,通过游标变量提高效率
- 遍历相关的成员函数是相互依赖,相互配合的关系
- 封装结点的申请和删除操作更有利于增强扩展性
- 顺序表与单链表相结合后衍生出静态单链表
- 静态单链表是 LinkList 的子类,拥有单链表的所有操作
- 静态单链表在预留的空间中创建结点对象
- 静态单链表适合于频繁增删数据元素的场合( 最大元素个数固定 )
以上是关于数据结构开发:静态单链表的实现的主要内容,如果未能解决你的问题,请参考以下文章