可持久化线段树

Posted 2023-04-18

参考技术A 在这里，所谓“可持久化”的数据结构并非指将数据存在非易失的存储器上，而是指保存了数据修改的历史信息。比如说对可持久化线段树进行修改操作，操作完成后我们可以在线段树原有的时间复杂度内查询到希望查询的版本的信息，比如“第二次修改后区间L和R之间的和”。

通常遇到的线段树都是构建之后结构不变化的，所以在修改关键值时，只有节点内的值受到影响，而树本身的结构不发生变化（比如左右子节点所表示的区间）。这为线段树进行可持久化提供了便利。我们每次修改的时候不直接改动原来节点的值，而是创建一系列新的节点。如果整棵树复制的话不仅非常耗费时间，而且占用空间太大。在线段树的单次修改中，实际上受到影响的节点是有限的，原来的节点可以得到重复利用。

可持久化线段树每次修改都会自上而下地新建一些节点。每次修改后的版本都有一个根节点与之对应。

只考虑单点修改，我们将递归过程中所有的节点创建一个“影子节点”，所谓“影子节点”保存的是当前修改结束后的受到更改的值。当u是v的影子节点时，我们称v时u的原节点。

在线段树的修改操作中，子节点修改完成后只影响到父节点（pushup操作），而不会影响到兄弟节点。所以我们发现，当修改影响到非叶子结点u时，（在单点修改中）他一定只有一个子节点会受到修改的影响，比如右子节点受到影响，此时u的影子节点v的左子节点指向u的左子节点，而v的右子节点对应的是受到影响的新右子节点w，w是u的右子节点的影子节点，以此类推。

对于区间修改，需要维护一个lazy标签来推迟更新操作，在pushdown操作时，创建了u的原节点的子节点的影子节点，在实际实现中，通过维护一个节点的origin节点指针就可以做到这一点。

由于可持久化线段树在修改过程中需要不断新建影子节点，所以通常的下标标记子节点的方法不再有效。节点需要维护的不仅仅是线段树的关键值x，还有左右子节点指针lch、rch，lazy标记和原节点指针origin。

在修改线段树时，沿着最新版本的线段树自上而下地遍历、创建影子节点并修改即可。

下面的程序实现了一个维护区间和的可持久化线段树，支持区间修改。而且这个程序包含了一个demo。首先输入一个n，随后输入n个整数，表示a[1]~a[n]的初始值。随后开始查询和修改操作，输入q查询，m修改。查询接受一个版本号（从0开始），输出序列所有的值。修改接受u、v和w，表示将区间[u,v]每个元素加上w。

Have fun！

可持久化专题——浅谈主席树：可持久化线段树

前言

不得不说，可持久化数据结构真是太难了！

由于数据结构这东西真的太玄学了，学这个主席树我真的学了很久。

---

简介

主席树为什么叫主席树？据说因为它是一个名字缩写为(HJT)的神犇发明的，与当时主席的名字缩写一样......

主席树实质上就是一棵可持久化线段树，它的具体实现可以看下面。

---

让我们从值域线段树开始说起

要学主席树，我们就要先学值域线段树。

值域线段树的区间存的并不是节点信息，而是在值在某一范围内的数的个数。

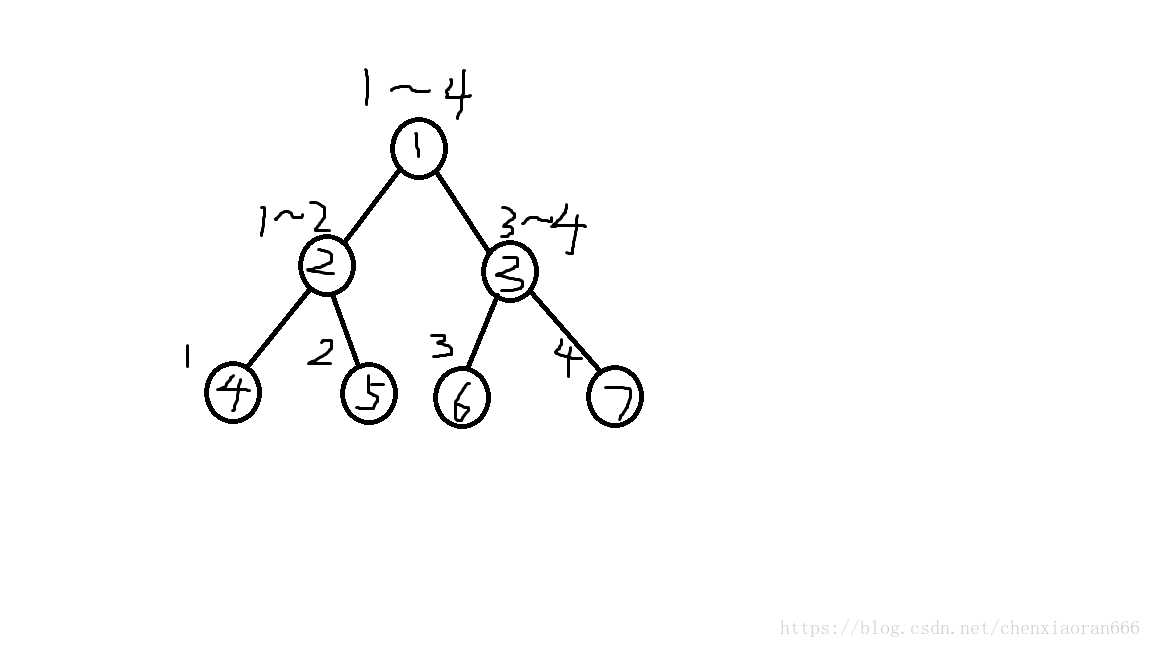
如图就是一棵值域线段树，其中1号节点存储的是大于等于1小于等于4的数字个数，2号节点存储的是大于等于1小于等于2的数字个数，3号节点存储的是大于等于3小于等于4的数字个数，4号节点存储的是等于1的数字个数，5号节点存储的是等于2的数字个数，6号节点存储的是等于3的数字个数，7号节点存储的是等于4的数字个数。

值域线段树的查询也挺简单的，若要查询这段区间内的第(k)大，只要比较当前元素的左子树大小加1（1是当前元素本身的大小）与询问的(k)，若大于等于，就访问左子树，否则将(k)减去当前元素的左子树大小加1，然后访问右子树。

这和平衡树有什么区别！！！

还有一个问题，就是值域线段树存储的区间范围是固定的，所以如果要查询区间第(k)大，我们就不能只用一棵值域线段树。

考虑建(n)棵值域线段树，每棵值域线段树存储区间([1,i])的信息，这样一来，要查询([l,r])的第(k)大时，只要在查询的过程中，将第(r)棵值域线段树的信息减去第(l-1)棵值域线段树的信息即可，这利用了前缀和的思想。
或许你会问，这有什么用？建(n)棵树，内存那么大，我平衡树第一个不服！

好吧，不服就不服，值域线段树还是有点用的，因为平衡树没法可持久化啊（可持久化(Treap)请走开）！

---

从值域线段树到主席树

知道了值域线段树，我们就可以开始尝试实现主席树了。

来研究一下下面两棵分别存储([1,3])和([1,4])区间信息的值域线段树（圆圈中为以该节点为根的子树大小）。

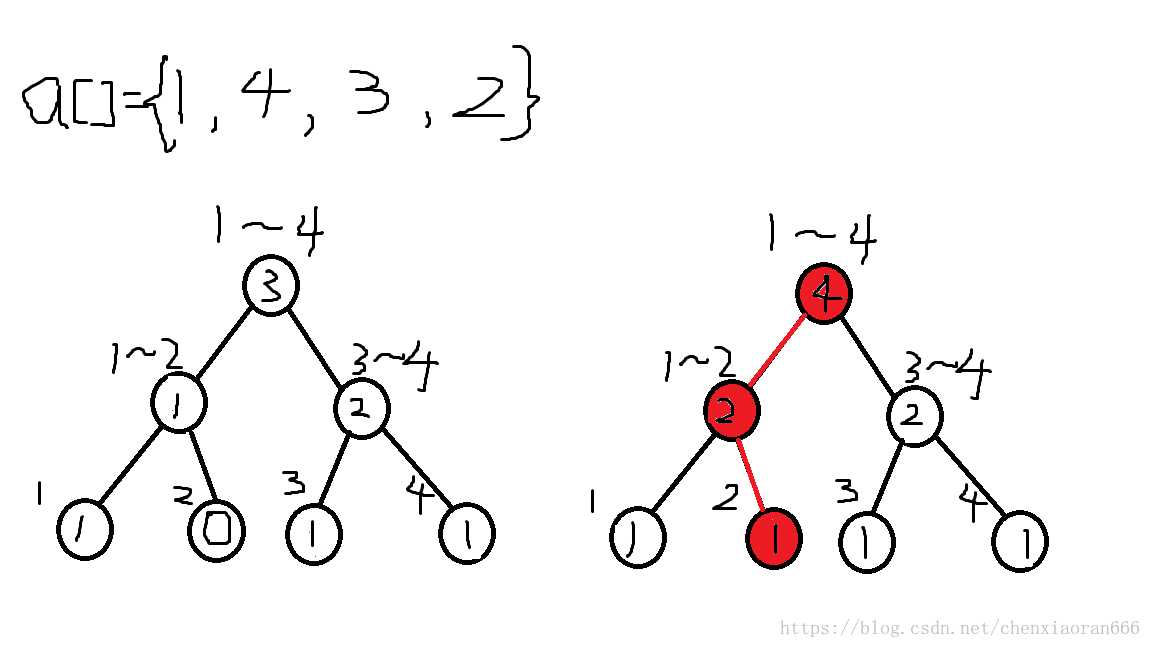
仔细观察可得，我们每次新加入一个节点，有影响的只有图中(color{red}{标红})的节点。

再仔细观察一下，这些节点都在一条链上（废话）。

那么，我们就会有一个大胆的想法：可不可以每次只新建一条链而不是一棵树，就像下面这样？

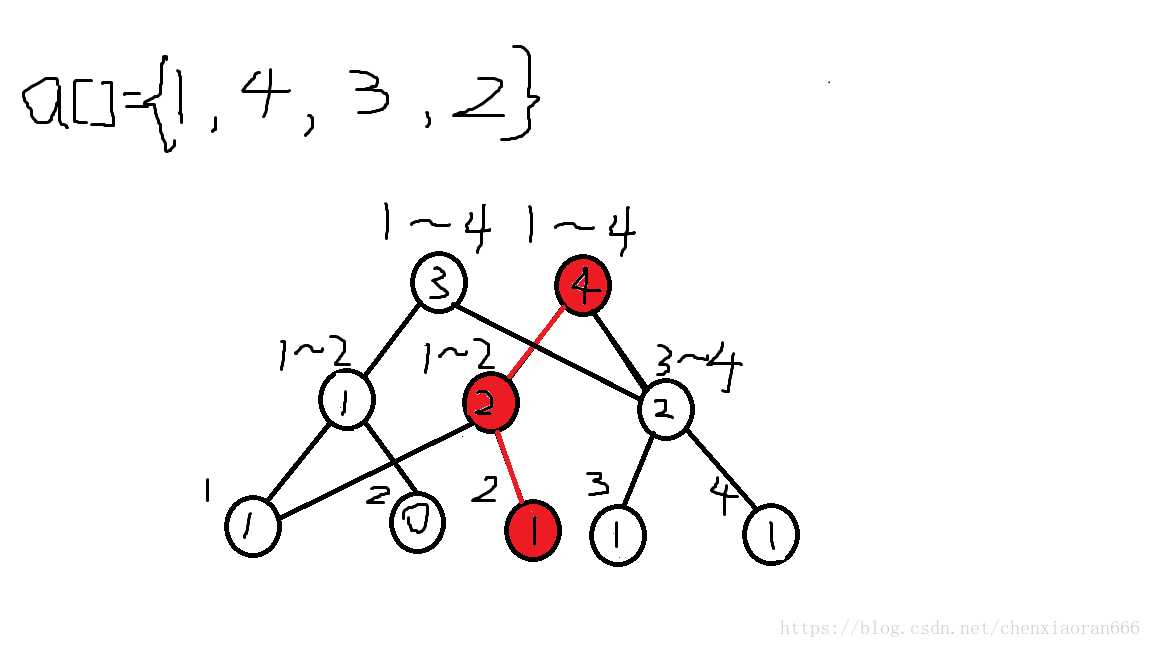
这就是传说中的主席树了。

---

主席树的具体实现

当然，真正实现主席树时，还是有一些细节要注意的。

这里就不多讲了，直接上代码吧：（洛谷板子题）

#include<bits/stdc++.h>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define LL long long
#define swap(x,y) (x^=y,y^=x,x^=y)
#define tc() (A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++)
#define pc(ch) (pp_<100000?pp[pp_++]=(ch):(fwrite(pp,1,100000,stdout),pp[(pp_=0)++]=(ch)))
#define N 200000 
int pp_=0;char ff[100000],*A=ff,*B=ff,pp[100000];
using namespace std;
int n,Q,m,tot=0,rt[N+5],a[N+5],p[N+5];
struct Chairman_Tree
{
    int Son[2],Size;
}node[N<<6];
inline void read(int &x)
{
    x=0;int f=1;char ch;
    while(!isdigit(ch=tc())) f=ch^‘-‘?1:-1;
    while(x=(x<<3)+(x<<1)+ch-‘0‘,isdigit(ch=tc()));
    x*=f;
}
inline void write(int x)
{
    if(x<0) pc(‘-‘),x=-x;
    if(x>9) write(x/10);
    pc(x%10+‘0‘);
}
inline void Build(int &rt,int l,int r)//建出一棵初始时的的树，和传统的线段树几乎一样
{
    rt=++tot;//新建一个节点，动态开点也是主席树中特别重要的
    int mid=l+r>>1;
    if(!(l^r)) return;
    Build(node[rt].Son[0],l,mid),Build(node[rt].Son[1],mid+1,r);//分别建树
}
inline void NewPoint(int &rt,int lst,int l,int r,int val)//新建一个节点（准确来说，应该是新建一条链）
{
    node[rt=++tot]=node[lst],++node[rt].Size;//动态开点，先复制原先的节点，然后将子树大小加1
    int mid=l+r>>1;
    if(!(l^r)) return;
    if(val<=mid) NewPoint(node[rt].Son[0],node[lst].Son[0],l,mid,val);//如果插入的新值比当前元素小（或等于），那么就新建一个左儿子
    else NewPoint(node[rt].Son[1],node[lst].Son[1],mid+1,r,val);//否则，新建一个右儿子
}
inline int Query(int rt1,int rt2,int l,int r,int k)//区间查询，相当于同时在两棵值域线段树上询问
{
    int mid=l+r>>1;
    if(!(l^r)) return l;//如果l与r相等，就返回l
    if(node[node[rt2].Son[0]].Size-node[node[rt1].Son[0]].Size>=k) return Query(node[rt1].Son[0],node[rt2].Son[0],l,mid,k);//如果当前左子树大小加1大于等于询问的k，那么访问左子树
    else return Query(node[rt1].Son[1],node[rt2].Son[1],mid+1,r,k-node[node[rt2].Son[0]].Size+node[node[rt1].Son[0]].Size);//否则，将k减去当前左子树大小加1
}
inline int num(int x)//求出一个数离散化后的值，一个二分的过程
{
    int l=1,r=m;
    while(l<=r)
    {
        int mid=l+r>>1;
        if(p[mid]==x) return mid;
        else if(p[mid]>x) r=mid-1;
        else l=mid+1;
    }
}
int main()
{
    register int i;
    for(read(n),read(Q),i=1;i<=n;++i) read(a[i]),p[i]=a[i];
    for(sort(p+1,p+n+1),Build(rt[0],i=1,m=unique(p+1,p+n+1)-p-1);i<=n;++i) NewPoint(rt[i],rt[i-1],1,m,num(a[i]));//将元素离散化，新建一棵树以及n条链，注意存储每条链的根节点的编号
    for(i=1;i<=Q;++i)//询问
    {
        int x,y,k;
        read(x),read(y),read(k),write(p[Query(rt[x-1],rt[y],1,m,k)]),pc(‘
‘);//利用前缀和思想
    }
    return fwrite(pp,1,pp_,stdout),0;
}