leetcode No518 零钱兑换Ⅱ java

Posted 2022-12-15 短腿Cat

题目

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:

输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2:

输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。

示例 3:

输入: amount = 10, coins = [10] 
输出: 1

注意:

你可以假设：
0 <= amount (总金额) <= 5000
1 <= coin (硬币面额) <= 5000
硬币种类不超过 500 种
结果符合 32 位符号整数

来源：力扣（LeetCode）
链接：leetcode No518 零钱兑换Ⅱ

---

题解

咱来分析分析题，其实题目意思就是：用一些硬币组合的值能等于一个他给定的数，要求我们计算有多少种组合。
我刚看到这道题的时候寻思这道题咋这么熟悉啊，突然想起来我做过类似的题：leetcode No39 组合总和 ，刚想上手直接dfs暴力解决，但是我看到这道题的数据范围之后，我直觉告诉我如果dfs是必定超时了，而且总用暴力办法是没有长进的，因此我抛弃了这种做法。
其实，这就是一道比较典型的动态规划题（对dp不太熟悉的小伙伴可以康康这篇博客，当初我就是看这个入门动态规划的dp入门），本题的 ‘人为分类’ 叫做：背包问题（如果对背包问题不太熟悉的小伙伴们，可以先了解了解背包问题，有dp基础的也可以直接往下看），因为假设每一种面额的硬币有无限个，更加细的分类的话我们叫这类题目为：完全背包问题。（其实无非就是动态规划，更细的分类对新手很友好，但是做过一两个基础的背包问题后应该要学会自己拓展做变式题，做不出再去看题解）

下面我们来分析本题

• 第一步：初始化dp数组：
  好的开头是成功的一半，第一步我们应该要确定dp数组是由什么组成的，很显然，这道题“硬币”就是基础背包问题的“物品”，硬币值就是“物品值”，所以dp的一个维度为硬币，再看，本题的“amount值”就是基础背包问题的“背包容量”，因此amount也应该设定为一个维度，因此dp数组有两个维度，是基于硬币和amount来得出的
  dp[i][j] 代表的含义：coins数组的前 i 个硬币能组合成 j 的组合数，因此我们的初始表得到了：
  

• 第二步：确定初始值：
  这此dp数组的初始值可不能乱赋，想想：有任意多个硬币，总共要0元的时候，答案是多少？答案是 1
  因为要0元的时候我们可以不选择任何硬币这样一种情况，因此dp[i][0]的值为1
  而当硬币为前0个（没有硬币）的情况，j无论为多少答案都是0，因此dp[0][j]为0
  所以有：
  
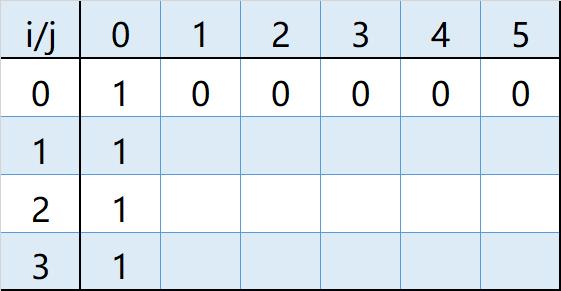
  注：我们可以在i的0、1、2、3右边标上其对应的硬币值方便我们考虑计算

• 第三步 分情况考虑，得出动态转移方程 （考虑dp[i][j]）

1. 在dp[i][j]中,当不选择下标为i的硬币时，dp[i][j]结果为dp[i - 1][j]（从前i个硬币变成前i - 1个硬币，最终要求得出的都是 j 值）
2. 在dp[i][j]中，当选择下标为i的硬币时，设下标为i的硬币值为val
   ①当取 1 个下标为i的硬币时的情况为：dp[i][j] = dp[i - 1][j - val*1]
   ②当取 2 个下标为i的硬币时的情况为：dp[i][j] = dp[i - 1][j - val*2]
   ③当取 3 个下标为i的硬币时的情况为：dp[i][j] = dp[i - 1][j - val*3]
   …
   ④当取 n 个下标为i的硬币时的情况为：dp[i][j] = dp[i - 1][j - val*n]
   注：j - val*n要求要大于0（上边界）（n取1时为下边界）

因此动态转移方程为：

• 不选择当前硬币时：dp[i][j]=dp[i-1][j]
• 选择当前硬币时：dp[i][j]=dp[i-1][j-n*val]

dp[i][j]中，因为不选择该硬币i时的情况和选择当前硬币时的n=0的情况相同，因此dp方程我们可以浓缩成一个式子：

dp[i]\\[j]=dp[i-1]\\[j-n*val]   ( 0≤n && j - n*val>=0 ) 即为： dp[i]\\[j]=dp[i-1]\\[j-n*val]   ( 0≤n && n<=j / val )

因此我们就可以编写程序了：

class Solution 
    public int change(int amount, int[] coins) 
        int len = coins.length;
        int[][] dp = new int[len + 1][amount + 1];
        //初始化面额为0的时候都是有1种方式（就是全都不选）
        for (int i = 0; i <= len; i++) 
            dp[i][0] = 1;
        
        for (int j = 1; j <= amount; j++) 
            for (int i = 1; i <= len; i++) 
                int val = coins[i - 1];//这里注意第i种硬币面值在coins数组中应为下标i - 1
                for (int n = 0; n * val <= j; n++) 
                    dp[i][j] += dp[i - 1][j - n * val];
                
            
        
        return dp[len][amount];
    

后续还有优化解法，之后会再更新，喜欢的看客们点个赞吧~