leetcode No279 完全平方数 java

Posted 2021-07-11 短腿Cat

题目

题解

刚看到这道题的时候，我的直觉就告诉我，肯定有很巧妙的数学办法，但是左思右想还是没想出来，算了，还是先上普通的解法吧。

万变不离其‘背包’—完全背包 朴素解法

与昨天的每日一题非常相似（题目作标：No518 零钱兑换Ⅱ 题解作标：No518超基础全方位入门本题）
这道题化成背包问题来看的话，背包问题的物品就是平方数（物品下标为i，体积为i*i）, 背包容量就是给定的数字n。表中i 和 j 分别表示，考虑从1 到 i 这些数中取平方数（比如1、2、3取得为1、4、9），这些平方数以最少的数量相加得到 j ，这个数量为多少。（假设j = 12，i = 3时，dp[i][j] = 3，原因是：12 = 4 + 4 + 4，一共有 3 个 4 组成）

那么问题来了，i 我们该如何取值呢？
实际上，既然要前 i 个数的平方值组成 j 的话，那么最大值 i 的平方数就不可以超过j，因此边界条件为 i * i ≤ j。

假设n值为13，则因此dp表格为：

注：dp[i][0]初始化为0很好理解，至于为什么dp[0][j]初始化为n的原因，先推出动态转移方程再细说 边界问题。

本题推出动态转移方程的核心思想其一就是 dp[i][j] 中j这一项要大于0，现在我们来分步骤考虑：

• 在dp[i][j]中，当不选择下标为i的平方数时，dp[i][j]结果为dp[i - 1][j]（因为不考虑为i的这个数，所以dp[i][j]的答案肯定由前i - 1个数得出）
• 在dp[i][j]中，当选择下标为 i 的平方数时，设 x 等于 i 的平方数（x = i * i），有如下情况：
  ①当取 1 个下标为i的平方数x时，情况为：dp[i][j] = dp[i - 1][j - x] + 1 （减掉1个x，剩余的值由前i - 1个数得出）
  ②当取 2 个下标为i的硬币时的情况为：dp[i][j] = dp[i - 1][j - x*2] + 2 （减掉2个x，剩余的值由前i - 1个数得出）
  ③当取 3 个下标为i的硬币时的情况为：dp[i][j] = dp[i - 1][j - x*3] + 3 （减掉3个x，剩余的值由前i - 1个数得出）
  … (令a = j - x*n ，要保证dp[i][a] 中的a是要大于0的)
  ④当取 m 个下标为i的硬币时的情况为：dp[i][j] = dp[i - 1][j - x*n] + m （减掉n个x，剩余的值由前i - 1个数得出）
  由上述可知，一共有n种情况，我们的dp[i][j]到底该取哪一种情况呢？题目要求我们要“最少能有多少平方数组成”，因此我们应该取这m种情况的最小值，即为：dp[i][j] = min( dp[i-1][j - x], dp[i-1][j - x * 2], … , dp[i - 1][j - x * m] )

将（选择当前下标 i 的情况）和（不选择当前下标 i 的情况）一起考虑，最终的动态转移方程为：
dp[i][j] = min( dp[i-1][j], dp[i-1][j - x] + 1, dp[i-1][j - x * 2] + 2, … , dp[i - 1][j - x * m] + m )
（ j - x * m >= 0 ）
得到的最终表为：

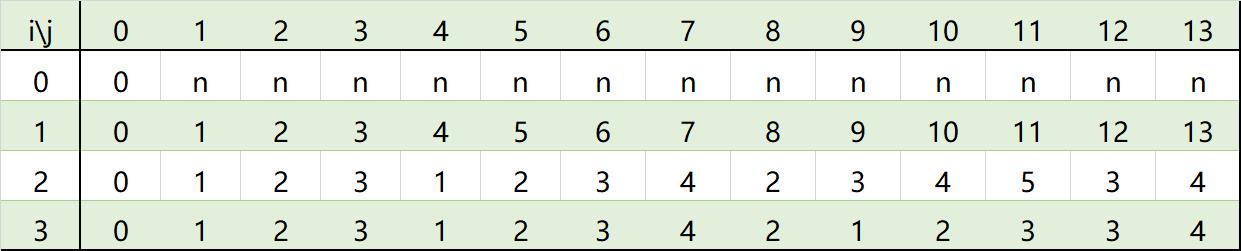
然后返回其dp[3][13]即可

边界问题 ： 昨天经过小伙伴的提醒，我注意到初始化值这一块也需要注意注意这里解释一下为什么dp[0][j]初始化为n的原因：

1. 有意义性：我们初始化的时候必须先判断当前初始化的数是否有意义，比如：

   ①dp[[i][0]表示有前i个数的平方相加得到0，最少需要多少个数，这非常显而易见，就是需要0个；
   ②dp[0][j]，前0个数的平方相加最少可以得到 j 值；当j为0的时候，可以取到dp[0][0]答案就是；当 j 不为0的时候，无论如何取值都不能让0的平方和等于一个不为0的数，因此我们发现，j>0,i=0的情况下dp无意义，
   
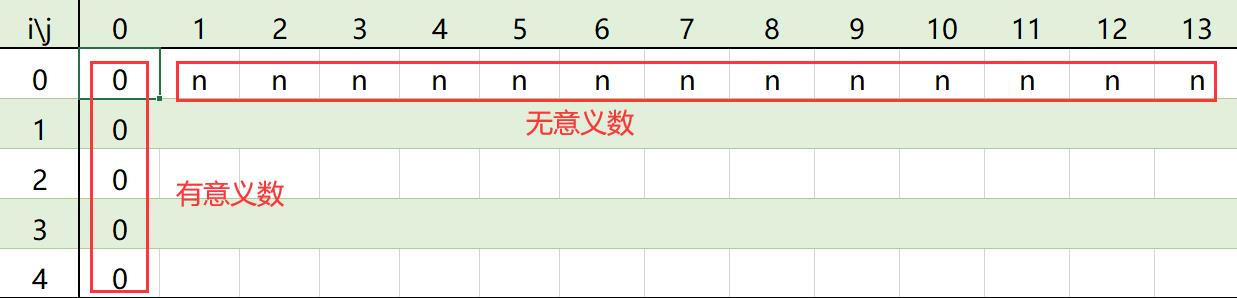
   既然无意义的话可以随便赋值了吗，不可以，应该怎么赋值呢，我们接着下一条赋值原则来讲。

2. 初始化值需要遵循一个原则，即“无后效性”，意思说的就是，之后计算dp[i][j]如果要用到这些值的话，这些值必须对计算结果不产生错误的影响，比如我们计算：dp[1][1] 因为要判断上述dp方程的一堆数里的最小值，那么我们初始化的dp[0][j]就不能比我们计算出来的其他值还要小，所以我们要让要让dp[0][j]在一定范围尽可能大，不然最小值取得的是我们初始化的一个数，产生了错误的结果，就无意义了。那么既然要让dp[0][j]尽可能大，能让他等于int类型的最大值吗，这是不可以的，为什么呢？

3. 基于本题的特殊性，我们来看动态转移方程，计算 dp[i][j]，需要用到 dp[i - 1][j - x * m] + m，既然有一个 + m，假设当前dp[i - 1][j - x * m]值就为int最大值，如果再让其+m就会溢出！
   
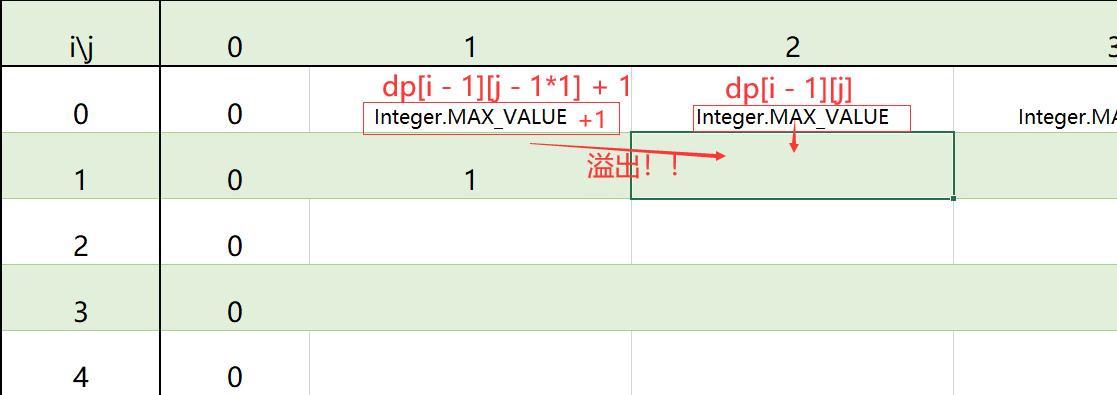
   因此我们不能让其等于int最大值；再看，我们在表中取值最大只能取到n（n 由 n 个 1 的平方数 组成），因此我们初始化其为n即可，也可以赋值一个不会溢出的数，如三叶姐初始化为0x3f3f3f3f，这样一个不会溢出的数。

朴素解法的答案为：

public int numSquares(int n) {
        int row = 0;
        for (row = 0; row * row < n; row++) {
        }
        int[][] dp = new int[row + 1][n + 1];

        for (int i = 1; i <= n; i++)
            dp[0][i] = n;

        for (int i = 1; i <= row; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = dp[i - 1][j];
                for (int a = 1; j - a * i * i >= 0; a++)
                    dp[i][j]= Math.min (dp[i][j], dp[i - 1][j - a * i * i] + a);
            }
        }
        return dp[row][n];
    }

但是很抱歉，这种写法是会超时的，但是我们可以学到这个题的主要思想，运用这个思想来进行优化，这就是我们下一步要说的优化解法。

完全背包 —进阶解法

任何从原始dp数组求得解的dp题，都是可以进行优化的，而本题的优化非常巧妙我们来看动态转移方程式（右边有m+1项）：

如果将j 替换成 j - x ，则表达式如下。（右边有m项）

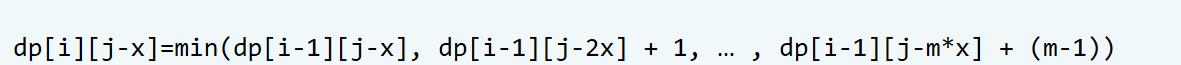
两式子放在一块儿对比，我们发现颜色相同的部分的值是相等的：

如果将dp[i][j-x]加1，就可以有如下代替：

由此得出dp[i][j] = min(dp[i - 1][j], dp[i][j - x] + 1),然后就可以进行i的维度的消去，写成：

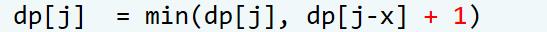
注：min中的dp[j]就是未更新的dp[j]，外部的dp[j]就是更新后的dp[j].

由此我们可以编写出代码：

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, 0x3f3f3f3f);
        dp[0] = 0;
        for (int i = 1; i * i <= n; i++) {
            for (int j = i * i; j <= n; j++) {
                if (j - i * i >= 0)
                    dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
            }
        }
        return dp[n];
    }
}

还有一种我最开始提过的解法，即数学结论法，这个方法之后我有时间再写一篇题解专门说一说吧
后话
套路是死的，但是题目却是活的，刷题过程中学一学套路呀模板什么的并没什么问题，但是最主要的是要能通过这些模板，将其转换成自己的内在的思想，这个才是真正能学到的东西，我们共同刷题的路上一起进步哦。

---

今日的题解已经送达，客观还喜欢吗，有疑问的话欢迎一起讨论嗷