《从零开始：机器学习的数学原理和算法实践》chap1

Posted 2022-12-14 临风而眠

《从零开始：机器学习的数学原理和算法实践》chap1 学习笔记

文章目录

• 《从零开始：机器学习的数学原理和算法实践》chap1 学习笔记
• • chap1 补基础：不怕学不懂微积分
  • 1.1 深入理解导数的本质
  • • 直观理解复合函数求导
  • 1.2 理解多元函数偏导
  • 1.3 理解微积分
  • 1.4 泰勒公式
  • 参考资料

chap1 补基础：不怕学不懂微积分

绝大多数机器学习算法在训练或者预测时会碰到最优化问题，而最优化问题的解决需要用到微积分中函数极值的求解知识

1.1 深入理解导数的本质

• 书中这两个挺有意思的

  • 哲学层面理解变化

    • 古希腊”飞矢不动“的论断
      • 该论断认为飞行的箭每一时刻必然位于空中的一个特定位置，每一瞬间都是静止的，既然每一瞬间都是精致的，那么飞行的箭就是”静止不动“的
    • 日常我们使用”运动“概念的时候，会牵涉时间、位置两个因素
      • ”每一瞬间箭都是静止的“这句话有问题
        • 每一瞬间就是每个时刻，每个时刻都会处于某个位置上，但是“静止”是一个跟“时间段”有关联的概念，不存在某个时 刻是“静止”还是“运动”的说法
        • 为了更好地刻画”运动“或”变化“，数学中引入了函数的概念

  • 生活中处处有函数

    • 下面是书中原话，我觉得很好玩

      ​ “你是你吗?”时刻$t_1$看到这句话的你跟时刻$t_2$开始思考这句话的你，难道没有发生变化吗?显然，时刻$t_2$的你已经不是时刻$t_1$的你了，但是大家并不会因此觉得“你不是你”。更一般地说，小时候的你跟现在的你相比，样貌、思想、行为、爱好都存在很大的不同，但是你并不会觉得小时候的你不是你。所以，什么是你呢?
      ​ 我们知道，任何事物都处于时间的河流之中，时间就像河流一样滚滚向前，不断流逝。所以，你可以被看成一个以时间为自变量、自身状态为因变量的函数，自变量的取值范围是你的寿命，而你就是与时刻对应的无穷多状态的总和。
      ​ 你在不同时刻有着不同的状态，我们为什么又会认为不同状态下的你是同一个“你”呢?这其实可以用连续函数来解释。虽然不同时刻的你对应着不同的状态，但是相邻时刻对应的状态差别很小，并且随着时刻越来越接近，状态差别也越来越小，这就是函数的连续性。这很好理解，例如用你读到这段话前后的时刻来对比，你的状态差别很小，别人也不会奇怪地对你说“你变了”;可是如果你跟几年未见的朋友再次见面，朋友可能就会发现你的变化。

• 从瞬时速度到导数

  • 导数典型的应用场景就是对瞬时速度的求解

    这里需要用到极限的概念
    

• 从近似运动来理解导数

  • 撇开极限的概念来理解

  • 寻找一个与变速运动最接近的匀速运动来求解

  • 不过不知道书上这段话是否全面，因为书上举的例子是二次函数的

    [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RkmajEB6-1669338352304)(https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20221125004819.png)]

直观理解复合函数求导

• 函数的主要复合方式

  • 函数相加
  • 函数相乘
  • 函数嵌套

• 感觉乘法法则讲的不错
  

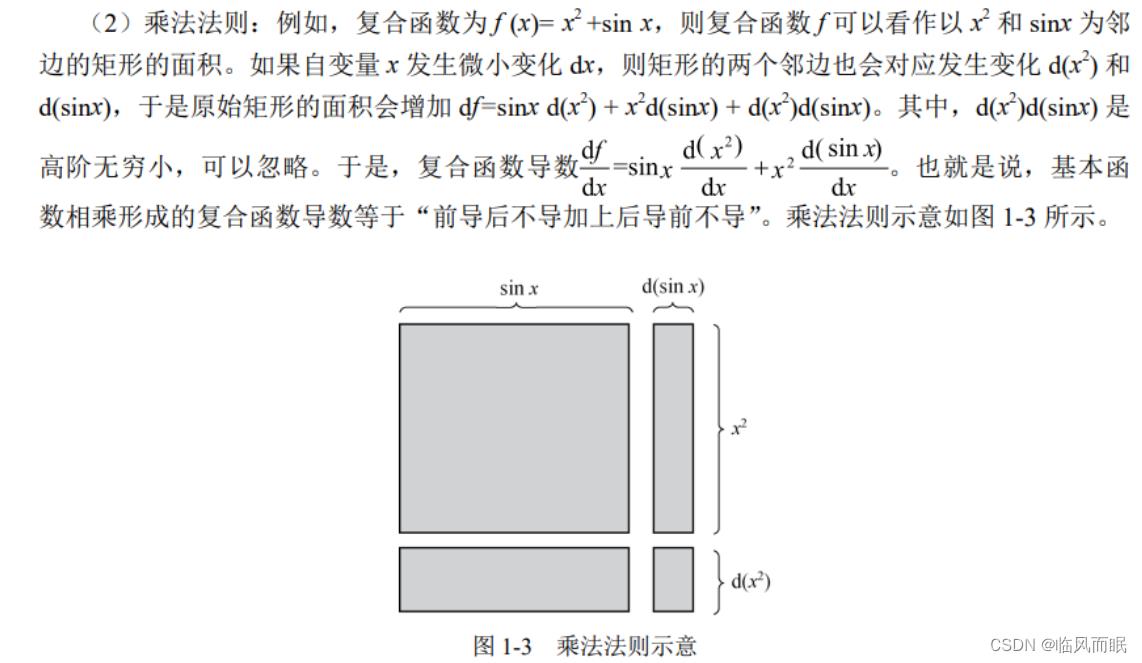
1.2 理解多元函数偏导

• 多元函数偏导数是什么

  • 求解方法：各个击破，对一个变量求导时，将其他变量暂时看成固定的参数
  • 保持其他变量固定而关注一个变量的微小变化带来的函数值变化情况，这种变化的比值就是偏导数

• 搞清楚梯度是什么

  • 梯度是导数对多元函数的推广，它是多元函数对各个自变量求偏导形成的向量

  • 梯度实际上是多变量微分的一般化

  • 梯度的本意是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）

  • 一般来说，梯度可以定义为一个函数的全部偏导数构成的向量

    • 突然联想到高中学物理的时候的”沿着电场强度方向，电势下降最快“

      • 去知乎上看了一些证明

        静电场中场强如何表示成点位的负梯度的？不要从环路积分往回推。就从电场强度的表达式进行直接的数学推导。？ - Sometimes Naive的回答 - 知乎 https://www.zhihu.com/question/41278859/answer/1477812184

        

      • 然后又在想 梯度下降肯定也能用到求电势的一些问题里面吧哈哈哈

1.3 理解微积分

书上是这样划分的，有一定道理

• 直观理解积分

  • 面积累加

• 直观理解微积分基本定理

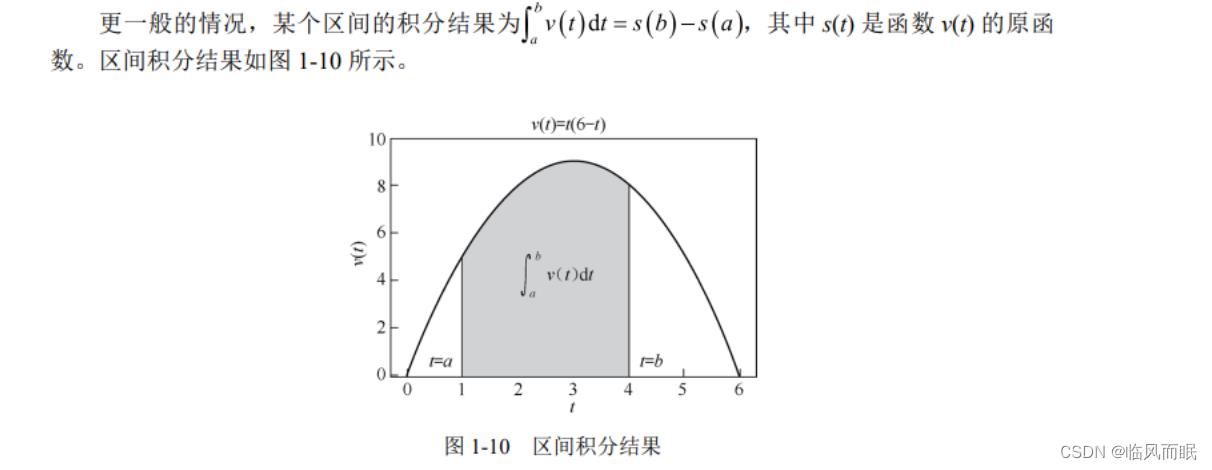
面积的差

如果函数 f(x) 在区间 [a, b] 上连续, 并且存在 原函数 F(x), 则 ${\int }_a^{b}f(x)\mathrm{d}x=F(b)-F(a)$ 。

1.4 泰勒公式

太真实了

• 泰勒公式是什么

  泰勒公式的典型形式如下:$f(x)=\frac{f(a)}{0!}+\frac{f^{\prime }(a)}{1!}(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\cdots +\frac{f^{(n)}(a)}{n!}(x-a{)}^n+R_n(x)$

  其中, $R_n(x)$ 是高阶无穷小量。上述公式也称为 f(x) 在点 a 处的泰勒级数。

  • 泰勒公式的主要作用是对特别复杂的函数进行化简, 具体来说就是通过近似函数来代替原函数, 通过使用简单熟悉的多项式去代替复杂的原函数。

• 直观理解泰勒公式

  • 多项式函数具有很好的性质，如易于计算、求导和积分等，所以如果能够用多项式函数来 近似代替一些复杂函数，那样很多问题就好解决了

  • 泰勒公式在实践中有着大量而广泛的应用，是数学中广泛应用的 函数近似工具。泰勒公式常见的应用场景是在某个点附近用多项式函数去逼近某个复杂的函数， 从而通过多项式函数在该点处的数值去获得复杂函数在该点处的近似值

  • 书上的例子蛮好的

  • 
    

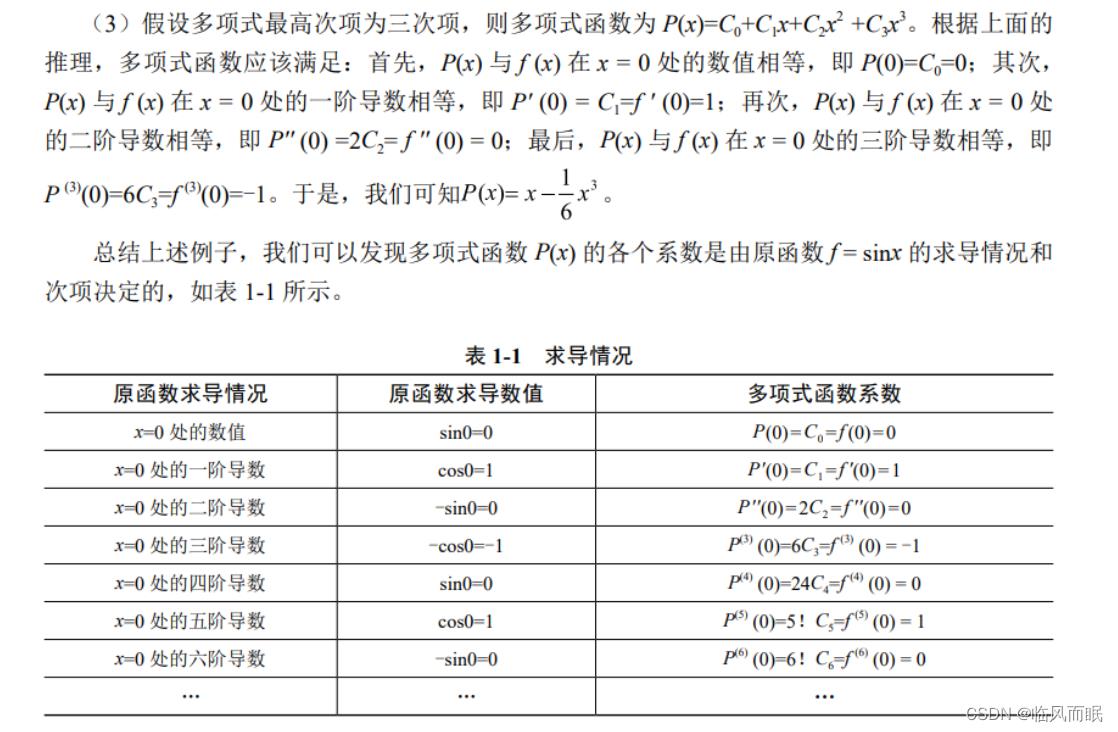
• 微积分基本定理与泰勒公式的关系

  • 感觉很妙
  • https://baijiahao.baidu.com/s?id=1668076072865336256&wfr=spider&for=pc

参考资料

• 《从零开始：机器学习的数学原理和算法实践》