Style Transfer from Non Parallel Text by Cross Alignment
Posted Facico
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Style Transfer from Non Parallel Text by Cross Alignment相关的知识,希望对你有一定的参考价值。
Style Transfer from Non Parallel Text by Cross Alignment
-
引入一个跨语料库(两个语料库有相同的content,但数据非并行)且能精确对齐的表达
-
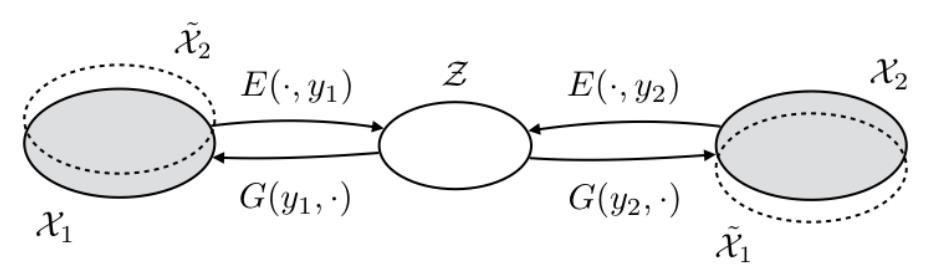
学习一个encoder,可以把input映射到一个与style无关的content表达。再将其传递给与style有关的decoder解码。
-
不用VAE(变分自编码器),因为我们需要使潜在content表达更丰富与自然
-
三个任务:情感转化,单词替换密码的破译,恢复语序
-
和CV的风格转化一样的有相似的结构
-
很多NLP任务都要并行数据,我们这里不用并行数据,而是从间接的训练信号信号引导句子生成
-
和前人的工作相似的:通过学习解开潜在表示来生成带可控属性的句子。他们的模型建立在VAE上并用独立约束使得我们可以从生成的句子推断出属性
-
我们这里的约束可以用同样的方式添加
-
-
有很多技术用于解决由RNN生成的离散样本做对抗性训练的问题
- professor-force: 采用用teacher-force的训练和self-feeding的测试来减少差距的方法
- 通过使用2个连续松弛来近似离散采样过程,可以通过反向传播有效地优化训练过程
假设数据是由如下方式生成的
- 1、分布 p ( y ) p(y) p(y)生成潜在style变量y
- 2、分布 p ( z ) p(z) p(z)生成潜在content变量z
- 3、分布 p ( x ∣ y , z ) p(x|y,z) p(x∣y,z)生成数据x
对于
数
据
X
1
=
(
x
1
(
1
)
.
.
.
x
1
(
n
)
)
,
X
2
=
(
x
2
(
1
)
.
.
.
x
2
(
n
)
)
未
知
量
的
风
格
y
1
,
y
2
分
布
p
(
x
1
∣
y
1
)
,
p
(
x
2
∣
y
2
)
两
种
内
容
的
转
化
p
(
x
1
∣
x
2
;
y
1
,
y
2
)
,
p
(
x
2
∣
x
1
;
y
1
,
y
2
)
(
条
件
概
率
中
的
分
号
表
示
待
估
参
数
)
从
边
缘
分
布
还
原
联
合
分
布
p
(
x
1
,
x
2
∣
y
1
,
y
2
)
=
∫
z
p
(
z
)
p
(
x
1
∣
y
1
,
z
)
p
(
x
2
∣
y
2
,
z
)
d
z
数据\\quad X_1=(x_1^(1)...x_1^(n)),X_2=(x_2^(1)...x_2^(n))\\\\ 未知量的风格\\quad y_1,y_2\\\\ 分布\\quad p(x_1|y_1),p(x_2|y_2)\\\\ 两种内容的转化\\quad p(x_1|x_2;y_1,y_2),p(x_2|x_1;y_1,y_2)\\\\\\qquad(条件概率中的分号表示待估参数)\\\\ 从边缘分布还原联合分布\\quad p(x_1,x_2|y_1,y_2)=\\int_zp(z)p(x_1|y_1,z)p(x_2|y_2,z)dz
数据X1=(x1(1)...x1(n)),X2=(x2(1)...x2(n))未知量的风格y1,y2分布p(x1∣y1),p(x2∣y2)两种内容的转化p(x1∣x2;y1,y2),p(x2∣x1;y1,y2)(条件概率中的分号表示待估参数)从边缘分布还原联合分布p(x1,x2∣y1,y2)=∫zp(z)p(x1∣y1,z)p(x2∣y2,z)dz
- 这个还原是有缺陷的
- 假设边缘分布得到的 p ( x ∣ y 1 ) = p ( x ∣ y 2 ) , y 1 ≠ y 2 p(x|y_1)=p(x|y_2),y_1≠y_2 p(x∣y1)=p(x∣y2),y1=y2,那么x最后风格可以是 y 1 , y 2 y_1,y_2 y1,y2中的的任一个
- 所以上面的框架对任意不同的y_1,y_2满足
p
(
x
∣
y
1
)
≠
p
(
x
∣
y
2
)
p(x|y_1)≠p(x|y_2)
p(x∣y1)=p(x∣y2)才能成立
- 这同样说明对于不同的style y生成的x不同
- 同时,这很可能对简化的数据分布来说不成立,所以当我们的分布z越复杂,我们越可能从边缘分布还原联合分布
z的分布
高斯分布
先用最常用的标准正态分布 z ∼ N ( 0 , I ) z\\sim N(0,I) z∼N(0,I)
假设style y是一个仿射变换 y = ( A , b ) y=(A,b) y=(A,b)
- 有 x = A z + b + ϵ x=Az+b+\\epsilon x=Az+b+ϵ
- 那么对于 b = 0 b=0 b=0和任意正交矩阵满足 A , A z + b ∼ N ( 0 , I ) A,Az+b \\sim N(0,I) A,Az+b∼N(0,I),此时的 x x x对任意的 y = ( A , 0 ) y=(A,0) y=(A,0)有相同的分布。
- 在上面这种情况,因为这种可以旋转的影响,我们不能恢复分布
混合高斯分布
- 不过对于一个复杂的分布,像混合高斯分布这样的,放射变换的形式可以被唯一确定
p ( z ) = ∑ k = 1 K π k N ( z ; μ k , Σ k ) K ≥ 2 , Σ i ≠ Σ j Y = ( A , b ) ∣ ∣ A ∣ ≠ 0 p ( x ∣ y , z ) = N ( x ; A z + b , ϵ 2 I ) 这 样 对 于 两 个 不 用 y 就 有 p ( x ∣ y 1 ) ≠ p ( x ∣ y 2 ) p(z)=\\sum_k=1^K \\pi_k N(z;\\mu_k,\\Sigma_k)\\qquad K\\geq 2,\\Sigma_i \\not= \\Sigma_j\\\\ Y=\\left\\(A,b)||A|\\not=0\\right\\\\\\ p(x|y,z)=N(x;Az+b,\\epsilon^2I)\\\\这样对于两个不用y就有p(x|y_1)\\not=p(x|y_2) p(z)=k=1∑KπkN(z;μk,Σk)K≥2,Σi=Σj以上是关于Style Transfer from Non Parallel Text by Cross Alignment的主要内容,如果未能解决你的问题,请参考以下文章
Non-resolvable parent POM for com.example:dubbo:0.0.1-SNAPSHOT: Could not transfer artifact org.spri
基于window7+caffe实现图像艺术风格转换style-transfer