数字信号处理相关4(FPGA实现FIR滤波器)
Posted Times_poem
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字信号处理相关4(FPGA实现FIR滤波器)相关的知识,希望对你有一定的参考价值。
来自:https://blog.csdn.net/u014783685/article/details/74466107
1、FIR滤波器总体设计
本设计是基于FPGA实现一个8阶的FIR数字低通滤波器。本次设计首先利用MATLAB中的FDAtool工具设计出一个采样频率为5KHZ、截止频率为1KHZ的FIR低通滤波器,通过FDAtool导出8点系数,然后将系数进行放大、取整,以便于在FPGA中使用,最后通过QuartusII进行Verilog语言编写滤波器算法,然后通过Modesim仿真结果和MATLAB仿真结果的比较来验证该滤波器的正确性。系统的总体设计框图如下:
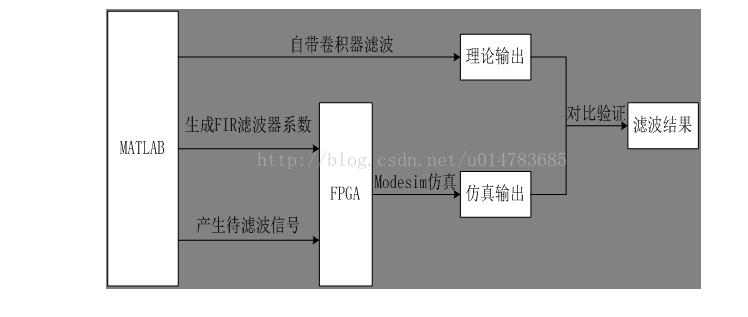
首先由MATLAB生成一个由三个正弦波叠加的待滤波信号,三个正弦波的频率分别是1KHZ,3KHZ,4KHZ。然后将待滤波信号送入Modesim仿真,观察滤波后的波形,再利用MATLAB里面的conv函数将滤波器系数和待滤波信号卷积并观察滤波后的波形图,将Modesim的仿真结果和MATLAB的仿真结果比较并验证在FPGA中滤波器算法的正确性。
2、FIR滤波器原理
在学习数字信号处理时,滤波器是重点,数字滤波器有很多种,比如FIR、IIR、LMS等滤波算法,FIR (Finite Impulse Response)滤波器的特点是它的冲击响应是有限的,它跟过去的信号无关,所以在使用时容易实现,速度快。
要理解FIR滤波器,需要知道信号的频域跟时域的关系,信号的频谱就是信号在频域上的表现形式,如果一个信号由2个正弦波叠加(图1)而成,我们在时域是看不出什么规律的,将信号进行傅里叶变换到频域(图2),我们就可以
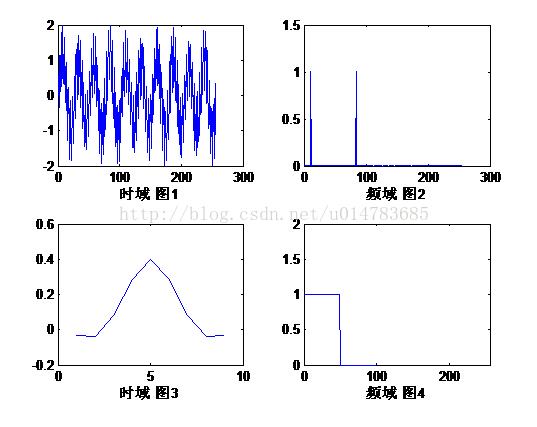
很清楚的看到该信号是由2个正弦波叠加而成的。
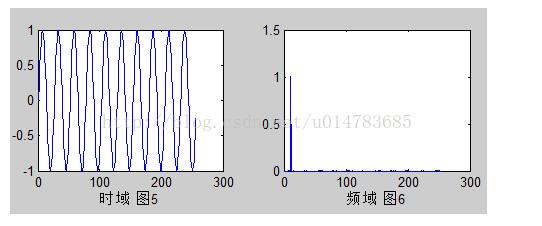
如果我们要对图1这个信号进行滤波,从频域上看,将信号的频谱乘以图4所示的矩形波,结果的频谱很显然就只剩下了低频段的这个正弦波,那么我们知道在频域和一个矩形波相乘就可以将高频滤出,在时域怎么做呢?我们学过信号与系统,知道频域卷积定理,这个定理的内容就是说:两个信号在频域相乘,那么在时域就相当于卷积,在时域相乘,在频域就相当于卷积。知道了这个定理,我们将图4的频域信号反变换到时域,变成图3所示的信号,我们将这个信号和图1的信号进行卷积,得到的结果就是图5所示的波形,这个波形的频谱如图6所示。这样我们便完成了对信号的滤波。
MATLAB中的FDAtool就是用来根据需要的滤波器生成图3所示的滤波器系数。
3、MATLAB生成信号
3.1滤波器系数设计
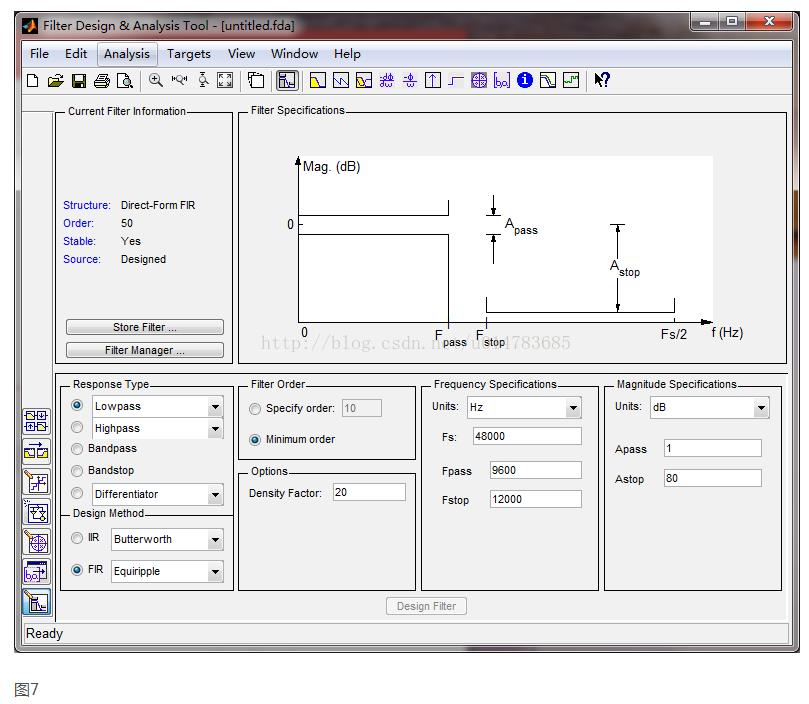
在MATLAB中输入fdatool即可打开滤波器设计工具,如图7所示。里面可以设置滤波器的类型,采样频率,截止频率等。本设计设置的参数如图8所示。
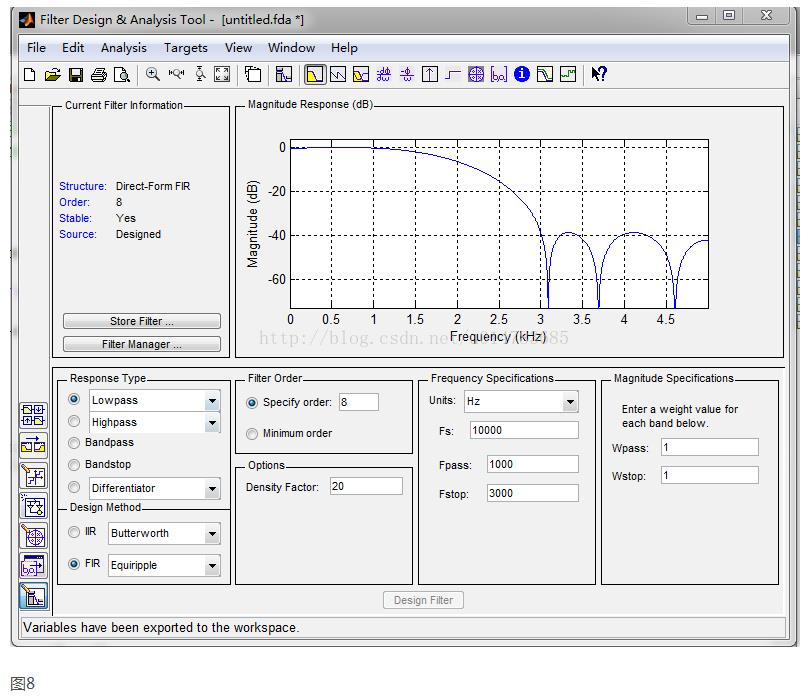
然后将此滤波器系数导出,然后用以下命令将系数放大、取整:
>> Num
Num =
-0.0325 -0.0384 0.0784 0.2874 0.3984 0.2874 0.0784 -0.0384 -0.0325
>> Num=round(Num*400)//将系数放大并取整
Num =
-13 -15 31 115 159 115 31 -15 -13
>> Num=Num+20//将系数符号变成正的,便于FPGA使用
Num =
7 5 51 135 179 135 51 5 7
最终生成的系数Num即可用于FPGA进行FIR滤波器实现。
3.2 待滤波信号的设计
本设计用于仿真的输入波形是三个正弦波叠加而成,分别是1KHZ、3KHZ、4KHZ。下面是用于生成待滤波信号的m文件内容:
%*********产生.data文件 用于FPGA仿真************%
Fs = 10000; %采样频率决定了两个正弦波点之间的间隔
N = 4096; %采样点数
N1 = 0 : 1/Fs : N/Fs-1/Fs;
s = sin(1000*2*pi*N1) + sin(3000*2*pi*N1) +sin(4000*2*pi*N1);//三种正弦波
fidc = fopen('D:\\FPGA\\FIR\\mem.txt','wt'); //将结果写入mem.txt文件,便于modesim使用
for x = 1 : N
fprintf(fidc,'%x\\n',round((s(x)+2.12)*58));
end
fclose(fidc);
4、FPGA实现FIR算法
实现FIR滤波器的过程其实就是实现卷积的过程,卷积的公式如下,从如下公式
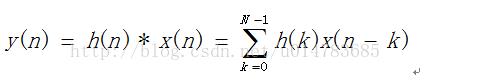
中可以看出,x(n)是我们的待滤波信号,h(n)是滤波器系数,卷积的过程其实就是一个乘、累加的过程,所以用FPGA实现8阶FIR滤波器的主要分成三级流水线,第一级、将输入信号延时,这样才能将信号和滤波器系数相乘。第二级、将输入信号和系数相乘。第三级、将乘积进行累加得到结果。
第一级流水线的实现代码如下:
reg[7:0] delay_pipeline1 ;
reg[7:0] delay_pipeline2 ;
reg[7:0] delay_pipeline3 ;
reg[7:0] delay_pipeline4 ;
reg[7:0] delay_pipeline5 ;
reg[7:0] delay_pipeline6 ;
reg[7:0] delay_pipeline7 ;
reg[7:0] delay_pipeline8 ;
reg[7:0] delay_pipeline9 ;
always@(posedge CLK or negedge RSTn)
if(!RSTn)
begin
delay_pipeline1 <= 8'b0 ;
delay_pipeline2 <= 8'b0 ;
delay_pipeline3 <= 8'b0 ;
delay_pipeline4 <= 8'b0 ;
delay_pipeline5 <= 8'b0 ;
delay_pipeline6 <= 8'b0 ;
delay_pipeline7 <= 8'b0 ;
delay_pipeline8<= 8'b0 ;
delay_pipeline9<= 8'b0 ;
end
else
begin
delay_pipeline1 <= FIR_IN ;
delay_pipeline2 <= delay_pipeline1 ;
delay_pipeline3 <= delay_pipeline2 ;
delay_pipeline4 <= delay_pipeline3 ;
delay_pipeline5 <= delay_pipeline4 ;
delay_pipeline6 <= delay_pipeline5 ;
delay_pipeline7 <= delay_pipeline6 ;
delay_pipeline8 <=delay_pipeline7 ;
delay_pipeline9<= delay_pipeline8 ;
end
这一级的功能是将输入信号进行延时,每到来一个时钟信号,便将输入信号保存到delay_pipelin1中,然后将剩下的依次移动一位。
第二级流水线的实现的部分代码如下:
wire[7:0] coeff1 = 8'd7; //滤波器系数
wire[7:0] coeff2 = 8'd5;
wire[7:0] coeff3 = 8'd51;
wire[7:0] coeff4 = 8'd135;
wire[7:0] coeff5 = 8'd179;
wire[7:0] coeff6 = 8'd135;
wire[7:0] coeff7 = 8'd51;
wire[7:0] coeff8 = 8'd5;
wire[7:0] coeff9 = 8'd7;
reg signed [16:0] multi_data1 ;//乘积结果
reg signed [16:0] multi_data2 ;
reg signed [16:0] multi_data3 ;
reg signed [16:0] multi_data4 ;
reg signed [16:0] multi_data5 ;
reg signed [16:0] multi_data6 ;
reg signed [16:0] multi_data7 ;
reg signed [16:0] multi_data8 ;
reg signed [16:0] multi_data9 ;
always@(posedge CLK or negedge RSTn) //x(0) * h(0)
if(!RSTn)
multi_data1 <= 17'b0 ;
else
multi_data1 <= delay_pipeline1*coeff1 ;
always@(posedge CLK or negedge RSTn) //x(1) * h(1)
if(!RSTn)
multi_data2 <= 17'b0 ;
else
multi_data2 <= delay_pipeline2*coeff2 ;
这一级的功能是将输入经过延时的信号和滤波器系数相乘,每到来一个时钟便将一个新的乘积结果更新到multi_data中。
第三级的实现代码如下:
//===================================================================
//加法器
//===================================================================
always@(posedge CLK or negedge RSTn)
if(!RSTn)
FIR_OUT <= 16'b0 ;
else
FIR_OUT <= multi_data1 + multi_data2 + multi_data3 + multi_data4 +multi_data5 + multi_data6 + multi_data7 + multi_data8 + multi_data9 ;
这一级的主要功能是将乘积累加,累加的结果就是滤波后的信号。
4、仿真结果
4.1 MATLAB仿真结果
本设计用MATLAB产生一个待滤波信号,然后将其和滤波器系数卷积,得到输出即为滤波后信号,MATLAB仿真的m文件内容如下:
Fs = 10000; %采样频率决定了两个正弦波点之间的间隔
N = 4096; %采样点数
N1 = 0 : 1/Fs :N/Fs-1/Fs;
in =sin(1000*2*pi*N1) + sin(3000*2*pi*N1) + sin(4000*2*pi*N1);
coeff =[-0.0325,-0.0384,0.0784,0.2874,0.3984,0.2874,0.0784,-0.0384,-0.0325];
out =conv(in,coeff);%卷积滤波
subplot(2,1,1);
plot(in);
xlabel('滤波前');
axis([0 200 -33]);
subplot(2,1,2);
plot(out);
xlabel('滤波后');
axis([100 200 -22]);
程序中的coeff就是用fdatool生成的滤波器系数,采样频率为10000,和设置fdatool时的采样频率必须一致,conv是MATLAB中的用来实现卷积的函数,它将待滤波信号in和coeff滤波器系数卷积,结果赋值给out,最后画出滤波前和滤波后的波形图,运行结果如下图所示:
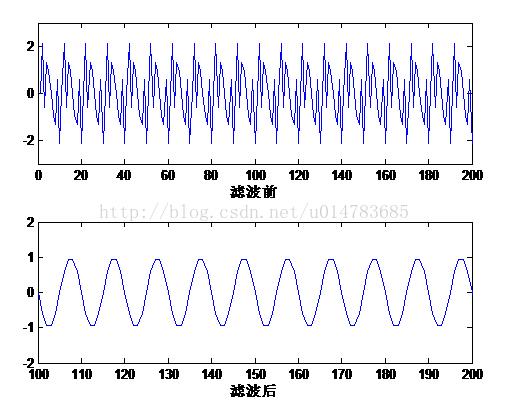
4.2 Modesim仿真结果
使用modesim仿真时,将第3节里面生成好的待滤波信号读入mem,然后仿真时将mem依次赋值给FIR_IN端口,仿真文件如下:
module FIR_vlg_tst();
reg CLK;
reg [7:0] FIR_IN;
reg RSTn;
reg [7:0] mem[1:4096];
wire [15:0] FIR_OUT;
reg [12:0] i;
FIR i1 (
.CLK(CLK),
.FIR_IN(FIR_IN),
.FIR_OUT(FIR_OUT),
.RSTn(RSTn)
);
initial
begin
$readmemh("D:/FPGA/FIR/mem.txt",mem);//将待滤波信号读入mem
RSTn= 0;
CLK= 0;
#50;
RSTn= 1;
#50000;
$stop;
end
initial
forever
#10 CLK = ~CLK;
always@(posedge CLK or negedge RSTn)
if(!RSTn)
FIR_IN <= 8'b0 ;
else
FIR_IN <= mem[i];
always@(posedge CLK or negedge RSTn)
if(!RSTn)
i <= 12'd0;
else
i <= i + 1'd1;
endmodule
在Quartus中运行Modesim软件,将输出设置为波形显示,仿真结果如下图:
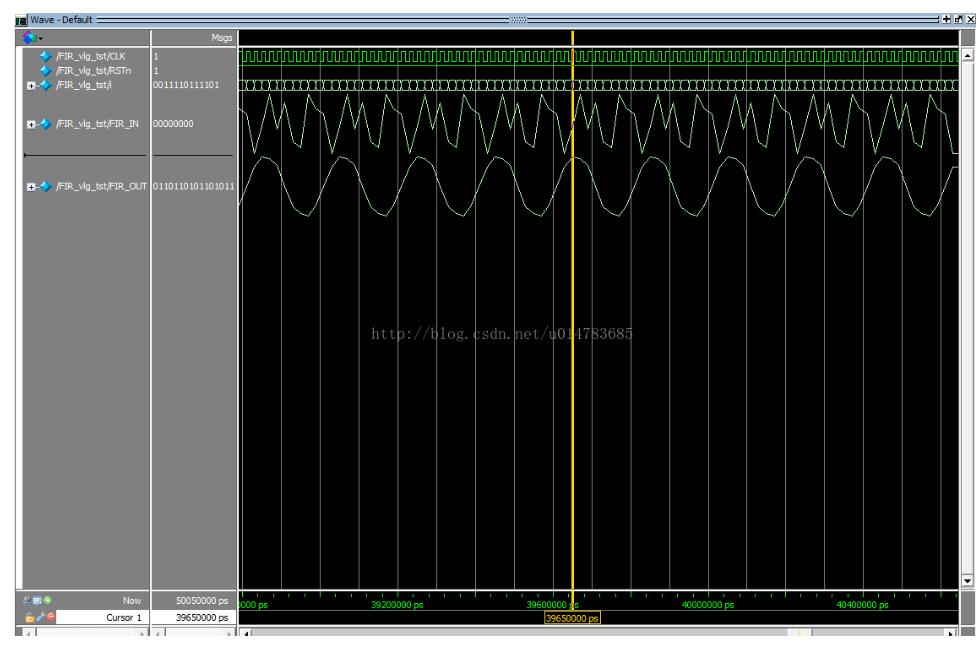
将上图和用MATLAB仿真的结果对比,两者完全一样,验证了在FPGA中的FIR滤波器算法。
---------------------
以上是关于数字信号处理相关4(FPGA实现FIR滤波器)的主要内容,如果未能解决你的问题,请参考以下文章