2022-10-27：设计一个数据结构，有效地找到给定子数组的 多数元素 。 子数组的 多数元素 是在子数组中出现 threshold 次数或次数以上的元素。 实现 MajorityChecker 类

Posted 2022-11-25 福大大架构师每日一题

2022-10-27：设计一个数据结构，有效地找到给定子数组的 多数元素 。
子数组的 多数元素 是在子数组中出现 threshold 次数或次数以上的元素。
实现 MajorityChecker 类:
MajorityChecker(int[] arr)
会用给定的数组 arr 对 MajorityChecker 初始化。
int query(int left, int right, int threshold)
返回子数组中的元素 arr[left…right] 至少出现 threshold 次数，
如果不存在这样的元素则返回 -1。

答案2022-10-27：

线段树。
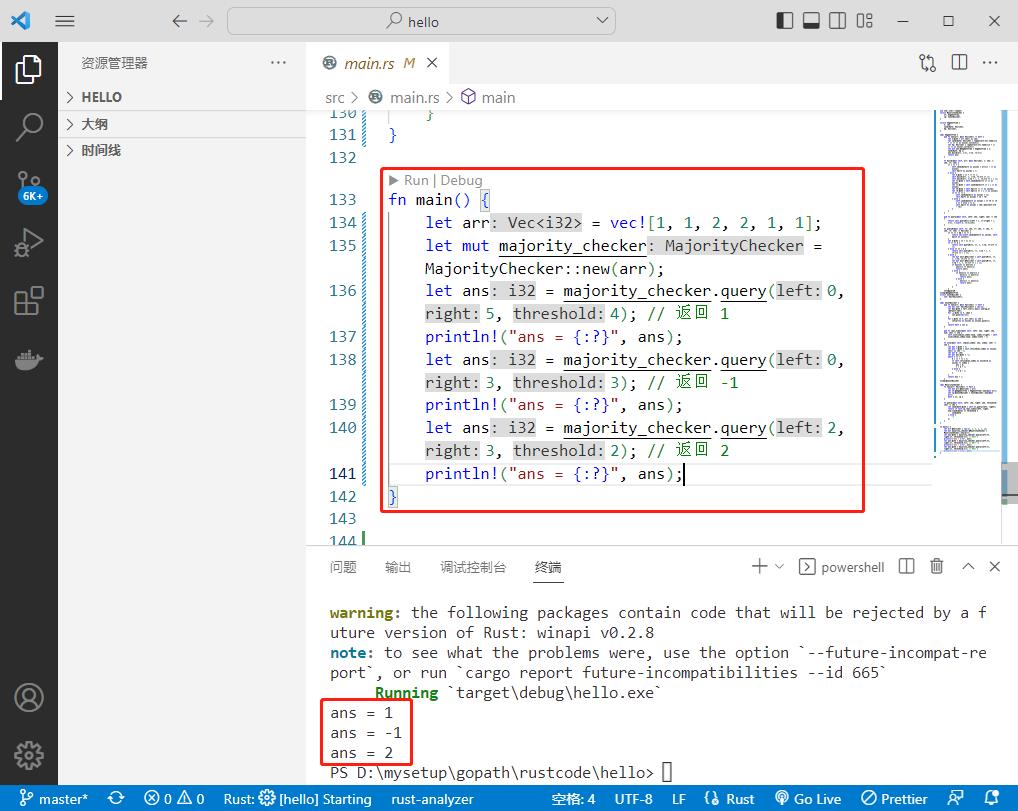
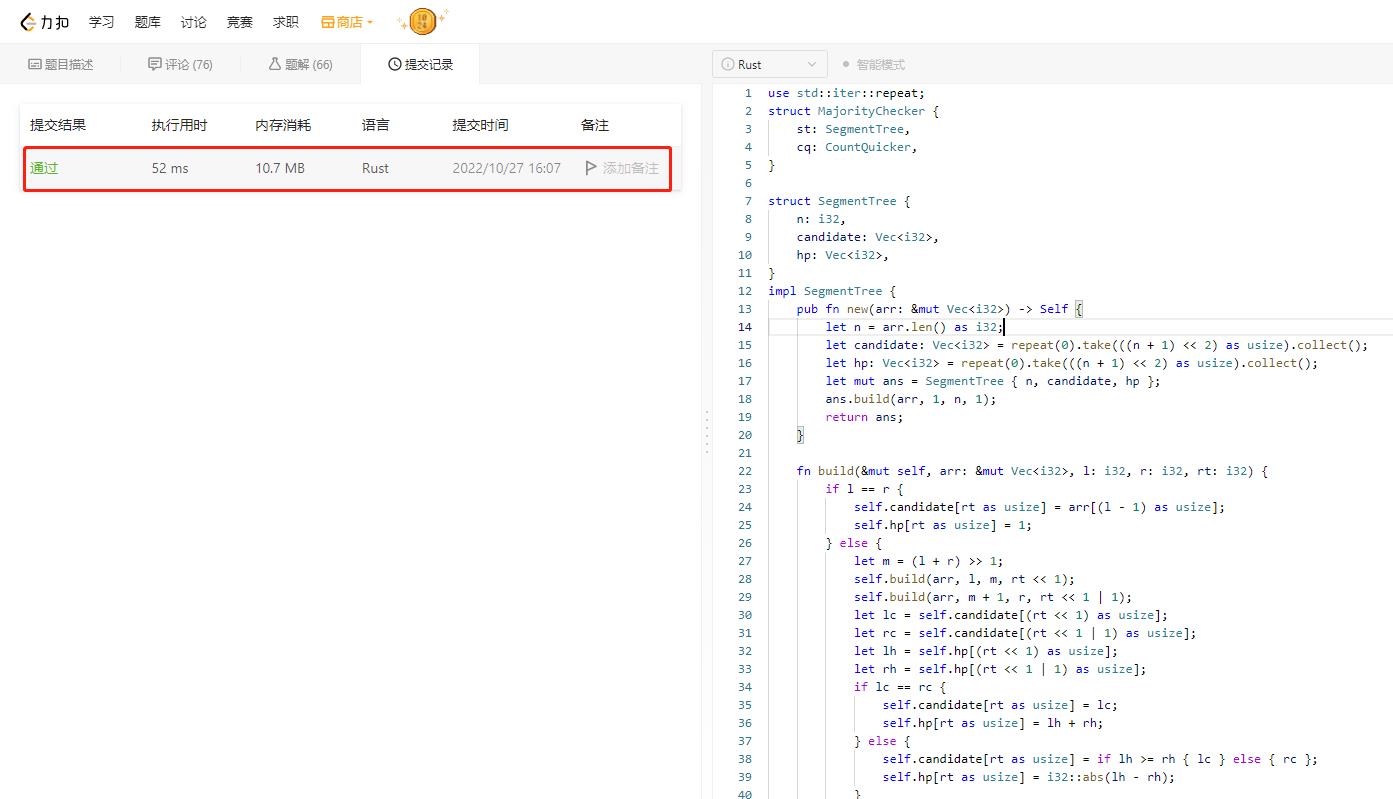
力扣1157，rust测试见图。

代码用rust编写。代码如下：

use std::iter::repeat;
struct MajorityChecker 
    st: SegmentTree,
    cq: CountQuicker,


struct SegmentTree 
    n: i32,
    candidate: Vec<i32>,
    hp: Vec<i32>,


impl SegmentTree 
    pub fn new(arr: &mut Vec<i32>) -> Self 
        let n = arr.len() as i32;
        let candidate: Vec<i32> = repeat(0).take(((n + 1) << 2) as usize).collect();
        let hp: Vec<i32> = repeat(0).take(((n + 1) << 2) as usize).collect();
        let mut ans = SegmentTree  n, candidate, hp ;
        ans.build(arr, 1, n, 1);
        return ans;
    

    fn build(&mut self, arr: &mut Vec<i32>, l: i32, r: i32, rt: i32) 
        if l == r 
            self.candidate[rt as usize] = arr[(l - 1) as usize];
            self.hp[rt as usize] = 1;
         else 
            let m = (l + r) >> 1;
            self.build(arr, l, m, rt << 1);
            self.build(arr, m + 1, r, rt << 1 | 1);
            let lc = self.candidate[(rt << 1) as usize];
            let rc = self.candidate[(rt << 1 | 1) as usize];
            let lh = self.hp[(rt << 1) as usize];
            let rh = self.hp[(rt << 1 | 1) as usize];
            if lc == rc 
                self.candidate[rt as usize] = lc;
                self.hp[rt as usize] = lh + rh;
             else 
                self.candidate[rt as usize] = if lh >= rh  lc  else  rc ;
                self.hp[rt as usize] = i32::abs(lh - rh);
            
        
    

    pub fn query(&mut self, left: i32, right: i32) -> i32 
        return self.query0(left + 1, right + 1, 1, self.n, 1)[0];
    

    fn query0(&mut self, ll: i32, rr: i32, l: i32, r: i32, rt: i32) -> Vec<i32> 
        if ll <= l && r <= rr 
            return vec![self.candidate[rt as usize], self.hp[rt as usize]];
        
        let m = (l + r) >> 1;
        if rr <= m 
            return self.query0(ll, rr, l, m, rt << 1);
         else if ll > m 
            return self.query0(ll, rr, m + 1, r, rt << 1 | 1);
         else 
            let mut ansl = self.query0(ll, rr, l, m, rt << 1);
            let mut ansr = self.query0(ll, rr, m + 1, r, rt << 1 | 1);
            if ansl[0] == ansr[0] 
                ansl[1] += ansr[1];
                return ansl;
             else 
                if ansl[1] >= ansr[1] 
                    ansl[1] -= ansr[1];
                    return ansl;
                 else 
                    ansr[1] -= ansl[1];
                    return ansr;
                
            
        
    

struct CountQuicker 
    cnt: Vec<Vec<i32>>,


impl CountQuicker 
    pub fn new(arr: &mut Vec<i32>) -> Self 
        let mut cnt: Vec<Vec<i32>> = vec![];
        let max = *arr.iter().max().unwrap_or(&0);
        for _i in 0..=max 
            cnt.push(vec![]);
        
        for i in 0..arr.len() as i32 
            cnt[arr[i as usize] as usize].push(i);
        
        return Self  cnt ;
    

    pub fn real_times(&mut self, left: i32, right: i32, num: i32) -> i32 
        self.size(num, right) - self.size(num, left - 1)
    

    fn size(&mut self, indies_index: i32, index: i32) -> i32 
        let mut l = 0;
        let mut r = self.cnt[indies_index as usize].len() as i32 - 1;
        let mut m: i32;
        let mut ans = -1;
        while l <= r 
            m = (l + r) / 2;
            if self.cnt[indies_index as usize][m as usize] <= index 
                ans = m;
                l = m + 1;
             else 
                r = m - 1;
            
        
        return ans + 1;
    


impl MajorityChecker 
    fn new(arr: Vec<i32>) -> Self 
        let mut arr = arr;
        let st = SegmentTree::new(&mut arr);
        let cq = CountQuicker::new(&mut arr);
        Self  st, cq 
    

    fn query(&mut self, left: i32, right: i32, threshold: i32) -> i32 
        let candidate = self.st.query(left, right);
        return if self.cq.real_times(left, right, candidate) >= threshold 
            candidate
         else 
            -1
        ;
    


fn main() 
    let arr = vec![1, 1, 2, 2, 1, 1];
    let mut majority_checker = MajorityChecker::new(arr);
    let ans = majority_checker.query(0, 5, 4); // 返回 1
    println!("ans = :?", ans);
    let ans = majority_checker.query(0, 3, 3); // 返回 -1
    println!("ans = :?", ans);
    let ans = majority_checker.query(2, 3, 2); // 返回 2
    println!("ans = :?", ans);

执行结果如下：

---

左神java代码