搜索算法
Posted 李憨憨_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了搜索算法相关的知识,希望对你有一定的参考价值。
搜索算法
文章目录
前言
搜索算法是去搜索每一个可能,主要分以下几种算法
- 枚举法:暴力搜索
- 深度优先搜索
- 广度优先搜索
- 回溯
深度优先搜索
我们先思考这样一个问题:
假如有编号为1~3的3张扑克牌和编号为1~3的3个盒子,现在需要将3张牌分别放到3个盒子中去,且每个盒子只能放一张牌,一共有多少种不同的放法。
- 当走到一个盒子面前的时候,到底要放那一张牌呢?在这里应该把所有的牌都尝试一遍。假设这里约定一个顺序,按牌面值从小到大依次尝试。在这样的假定下,当走到第一个盒子的时候,放入1号牌。
- 放好之后,继续向后走,走到第二个盒子面前,此时还剩2张牌,牌面值最小的为2号牌,按照约定的规则,把2号牌放入第二个盒子。
- 此时,来到第三个盒子面前,只剩一张牌,放入第三个盒子。此时手中的牌已经用完。
- 继续向后走,走到了盒子的尽头,后面再也没有盒子,并且也没有可用的牌了,此时,一种放法已经完成了,但是这只是一种放法,这条路已经走到了尽头,还需要折返,重新回到上一个盒子。
- 这里回到第三个盒子,把第三个盒子中的牌取出来,再去尝试能否再放其它的牌,这时候手里仍然只有一张3号牌,没有别的选择了,所以还需要继续向后回退,回到2号盒子面前。
- 收回2号盒子中的2号牌,现在手里有两张牌,2,3,按照约定,再把3号牌放入2号盒子,放好之后,继续向后走,来到3号盒子。
- 此时手里只有一张2号牌,把它放入3号盒子,继续向后走。
- 此时这条路又一次走到了尽头,一个新的放法又产生了,继续向上折返,尝试其它可能,按照上述步骤,依次会产生所有结果。
代码如何实现这种过程呢?最主要的事情,向面前的盒子里放每一种牌,一个for循环搞定。这里还需考虑,现在手里有没有这张牌,用一个数组book标记手里是否有这张牌
for(int i = 1; i <= n; i++)
if(book[i] == 0) //第i号牌仍在手上
boxs[index] = i;
book[i] = 1; //现在第i号牌已经被用了
面前的盒子处理完成之后,继续处理下一个盒子,下一个盒子的处理方法和当前一样。那么把上面的代码块封装一下,给它取一个名字,即为Dfs(Depth First Search)。
//index表示现在走到哪一个盒子面前
void Dfs(int index, int n, vector<int>& boxs, vector<int>& book)
for(int i = 1; i <= n; i++)
if(book[i] == 0) //第i号牌仍在手上
boxs[index] = i;
book[i] = 1; //现在第i号牌已经被用了
现在再去处理下一个盒子,直接调用Dfs(index + 1, boxs, book)即可。
void Dfs(int index, int n, vector<int>& boxs, vector<int>& book)
for(int i = 1; i <= n; i++)
if(book[i] == 0) //第i号牌仍在手上
boxs[index] = i;
book[i] = 1; //现在第i号牌已经被用了
//处理下一个盒子
Dfs(index + 1, n, boxs, book);
//从下一个盒子回退到当前盒子,取出当前盒子的牌,
//尝试放入其它牌。
book[i] = 0;
现在考虑什么时候得到一种方法呢,走到尽头,也就是第n+1个盒子的时候,表明前面的盒子已经放好牌了,这时候直接打印每个盒子中的牌即可。已走到尽头,向上回退。
void Dfs(int index, int n, vector<int>& boxs, vector<int>& book)
if(index == n + 1)
for(int i = 1; i <= n; i++)
cout<<boxs[i]<<" ";
cout<<endl;
return; //向上回退
for(int i = 1; i <= n; i++)
if(book[i] == 0) //第i号牌仍在手上
boxs[index] = i;
book[i] = 1; //现在第i号牌已经被用了
//处理下一个盒子
Dfs(index + 1, n, boxs, book);
//从下一个盒子回退到当前盒子,取出当前盒子的牌,
//尝试放入其它牌。
book[i] = 0;
完整代码
//完整代码
#include <vector>
#include <iostream>
using namespace std;
void Dfs(int index, int n, vector<int>& boxs, vector<int>& book)
if (index == n + 1)
for (int i = 1; i <= n; i++)
cout << boxs[i] << " ";
cout << endl;
return; //向上回退
for (int i = 1; i <= n; i++)
if (book[i] == 0) //第i号牌仍在手上
boxs[index] = i;
book[i] = 1; //现在第i号牌已经被用了
//处理下一个盒子
Dfs(index + 1, n, boxs, book);
//从下一个盒子回退到当前盒子,取出当前盒子的牌,
//尝试放入其它牌。
book[i] = 0;
int main()
int n;
vector<int> boxs;
vector<int> books;
cin >> n;
boxs.resize(n + 1, 0);
books.resize(n + 1, 0);
Dfs(1, n, boxs, books);
return 0;
从上面的代码可以看出,深度优先搜索的关键是解决"当下该如何做",下一步的做法和当下的做法是一样的。"当下如何做"一般是尝试每一种可能,用for循环遍历,对于每一种可能确定之后,继续走下一步,当前的剩余可能等到从下一步回退之后再处理。我们可以抽象出深度优先搜索的模型。
Dfs(当前这一步的处理逻辑)
1. 判断边界,是否已经一条道走到黑了:向上回退
2. 尝试当下的每一种可能
3. 确定一种可能之后,继续下一步 Dfs(下一步)
练习1:员工的重要性
https://leetcode-cn.com/problems/employee-importance/

边界: 下属为空
每次先加第一个下属的重要性
按照相同的操作再去加下属的第一个下属的重要性
class Solution
public:
void dfs(unordered_map<int, Employee*>& info, int& sum, int id)
//这里无需判断边界,for循环就是一个边界,下属为空,直接结束
sum += info[id]->importance;
for(const auto& subid : info[id]->subordinates)
dfs(info, sum, subid);
int getImportance(vector<Employee*> employees, int id)
if(employees.empty())
return 0;
unordered_map<int, Employee*> info;
//把员工信息用map存储,方便后面的使用
for(const auto& e : employees)
info[e->id] = e;
int sum = 0;
dfs(info, sum, id);
return sum;
;
class Solution
public:
int DFS(unordered_map<int,Employee*>& info, int id)
int curImpo = info[id]->importance;
for(const auto& sid : info[id]->subordinates)
curImpo += DFS(info, sid);
return curImpo;
int getImportance(vector<Employee*> employees, int id)
if(employees.empty())
return 0;
unordered_map<int,Employee*> info;
for(const auto& e : employees)
info[e->id] = e;
return DFS(info, id);
;
练习2:图像渲染
https://leetcode-cn.com/problems/flood-fill/
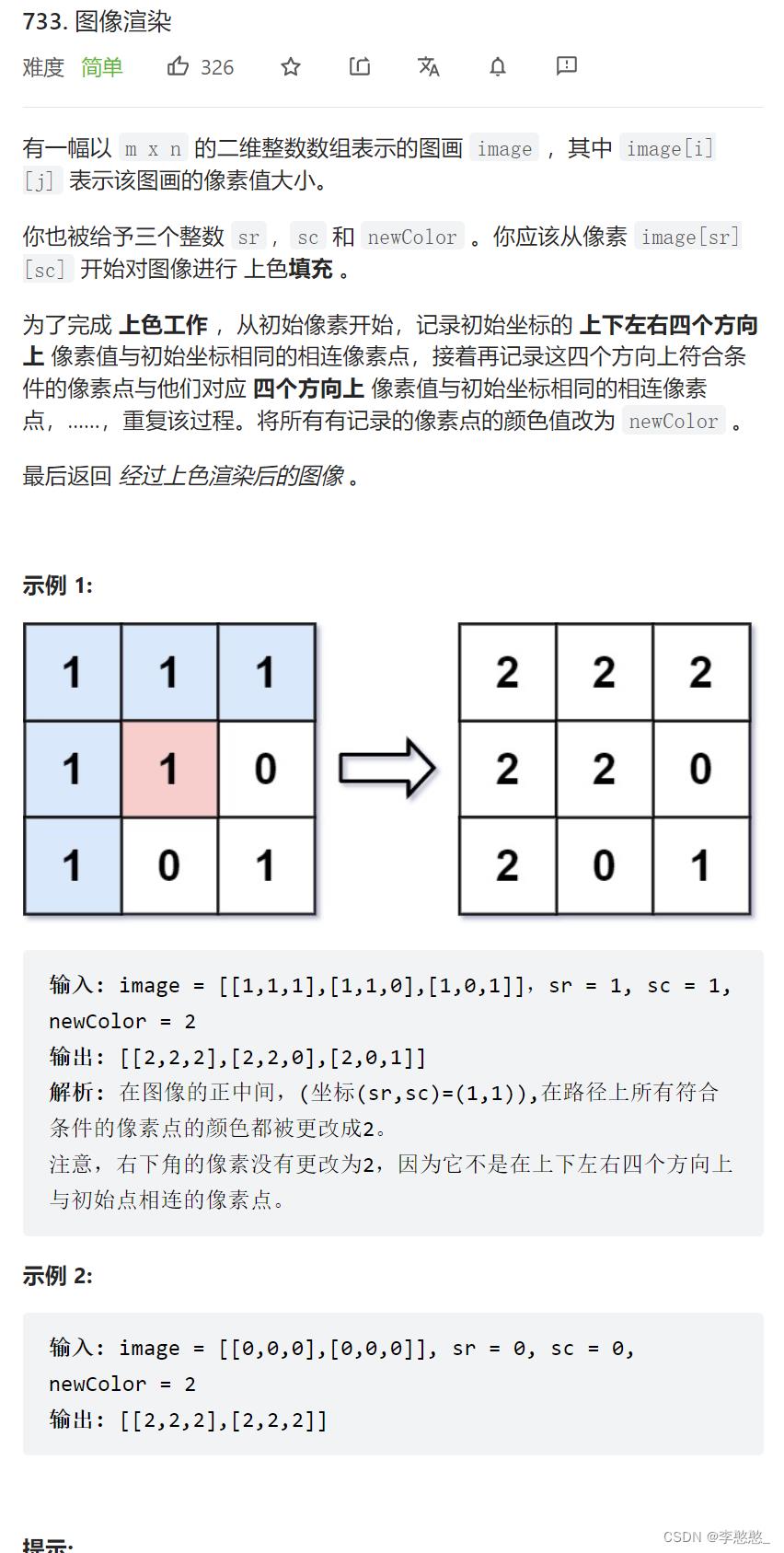
把和初始坐标开始,颜色值相同的点的颜色全部改为新的颜色
并且只要某个点颜色被更改,则继续以此点向周围渲染
比如题目的意思: 以位置(1,1)开始,向外渲染,只要渲染点的颜色值和(1,1)位置的颜色值相同,则继续向
外渲染
1 1 1
1 1 0
1 0 1
2 2 2
2 2 0
2 0 1
这里每一个符合要求的点都要向四个方向渲染
边界:位置是否越界
这里需要用的标记,避免重复修改,使时间复杂度不超过O(row * col)
#include <vector>
#include <iostream>
using namespace std;
//四个方向的位置更新:顺时针更新
int nextPosition[4][2] = 0, 1 , 1, 0 , 0, -1 , -1, 0 ;
class Solution
public:
void dfs(vector<vector<int>>& image, int row, int col, vector<vector<int>>& book, int sr, int sc, int oldColor, int newColor)
//处理当前逻辑,修改颜色,并且标记已经修改过了
image[sr][sc] = newColor;
book[sr][sc] = 1;
//遍历每一种可能,四个方向
for (int k = 0; k < 4; ++k)
int newSr = sr + nextPosition[k][0];
int newSc = sc + nextPosition[k][1];
//判断新位置是否越界
if (newSr >= row || newSr < 0 || newSc >= col || newSc < 0)
continue;
//如果颜色符合要求,并且之前也没有渲染过,则继续渲染
if (image[newSr][newSc] == oldColor && book[newSr][newSc] == 0)
dfs(image, row, col, book, newSr, newSc, oldColor, newColor);
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor)
if (image.empty())
return image;
int row = image.size();
int col = image[0].size();
//建立标记
vector<vector<int>> book;
book.resize(row);
for (int i = 0; i < row; ++i)
book[i].resize(col, 0);
//获取旧的颜色
int oldColor = image[sr][sc];
dfs(image, row, col, book, sr, sc, oldColor, newColor);
return image;
;
广度优先搜索
现在来思考这样一个问题, 迷宫问题:
假设有一个迷宫,里面有障碍物,迷宫用二维矩阵表示,标记为0的地方表示可以通过,标记为1的地方表示障碍物,不能通过。现在给一个迷宫出口,让你判断是否可以从入口进来之后,走出迷宫,每次可以向任意方向走。
- 假设是一个10*10的迷宫,入口在(1,1)的位置,出口在(8,10)的位置,通过(1,1)一步可以走到的位置有两个(1,2),(2,1)
- 但是这两个点并不是出口,需要继续通过这两个位置进一步搜索,假设现在在(1,2),下一次一步可以到达的新的位置为(1,3),(2,2)。而通过(2,1)可以一步到达的新的位置为(2,2),(3,1),但是这里(2,2)是重复的,所以每一个点在走的过程中需要标记是否已经走过了。
- 两步之后,还没没有走到出口,这时候需要通过新加入的点再去探索下一步能走到哪些新的点上,重复这个过程,直到走到出口为止。
代码解析这个过程,最关键的步骤用当前位置带出新的位置,新的位置可以存放在一个vector或者队列中。位置需要用坐标表示,这里封装出一个node。
struct node
int x;
int y;
;
//queue实现
bool Bfs(vector<vector<int>> graph, int startx, int starty, int destx, int desty)
//迷宫的大小
int m = graph.size();
int n = graph[0].size();
//存储迷宫中的位置
queue<node> q;
//标记迷宫中的位置是否被走过
vector<vector<int>> book;
book.resize(m);
for (size_t i = 0; i < m; i++)
book[i].resize(n, 0);
q.push(node(startx, starty));
//标记已经走过
book[startx][starty] = 1;
//四个行走的方向,上下左右
int next[4][2] = -1, 0 , 1, 0 , 0, -1 , 0, 1 ;
//标记是否可以出去
bool flag = false;
while (!q.empty())
//当前位置带出所有新的位置, 可以向上下左右走
for (size_t i = 0; i < 4; ++i)
//计算新的位置
int nx = q.front()._x + next[i][0];
int ny = q.front()._y + next[i][1];
//新的位置越界,继续下一个
if (nx >= m || nx < 0 || ny >= n || ny < 0)
continue;
//如果新的位置无障碍并且之前也没走过,保存新的位置
if (graph[nx][ny] == 0 && book[nx][ny] == 0)
q.push(node(nx, ny));
//标记已被走过
book[nx][ny] = 1;
//如果新的位置为目标位置,则结束查找
if (nx == destx && ny == desty)
flag = true;
break;
if (flag)
break;
//否则,用新的位置继续向后走
q.pop();
return flag;
//vector实现
bool Bfs(vector<vector<int>> graph, int startx, int starty,int destx, int desty)
//迷宫的大小
int m = graph.size();
int n = graph[0].size();
//存储迷宫中的位置
vector<node> queue;
queue.resize(m*n);
//标记迷宫中的位置是否被走过
vector<vector<int>> book;
book.resize(m);
for(size_t i = 0; i < m; i++)
book[i].resize(n, 0);
int head = 0;
int tail = 1;
queue[head].x = startx;
queue[head].y = starty;
//标记已经走过
book[startx][starty] = 1;
//四个行走的方向,上下左右
int next[4][2] = -1, 0, 1, 0, 0, -1, 0, 1;
//标记是否可以出去
bool flag = false;
while(head < tail)
//当前位置带出所有新的位置, 可以向上下左右走
for以上是关于搜索算法的主要内容,如果未能解决你的问题,请参考以下文章
[JavaScript 刷题] 搜索 - 腐烂的橘子, leetcode 994