Python机器学习笔记

Posted 2022-10-28 Python炭烧

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Python机器学习笔记相关的知识，希望对你有一定的参考价值。

Python机器学习笔记

一机器学习概述

1.1 人工智能概述

1.1.1 机器学习与人工智能、深度学习关系

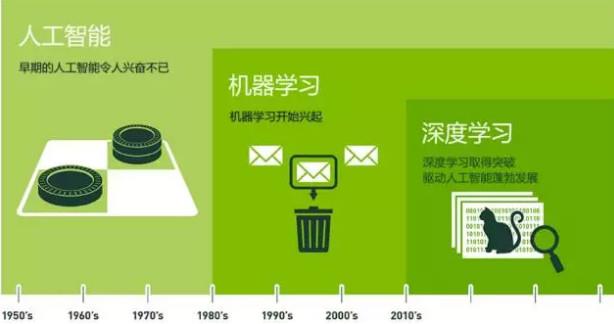
机器学习和人工智能、深度学习的关系
- 机器学习是人工智能的一个实现途径
- 深度学习是机器学习的一个方法发展而来
达特茅斯会议（Dartmouth Conferences）- 人工智能的起点

1956年，几个计算机科学家相聚在达特茅斯会议（Dartmouth Conferences），提出了“人工智能”的概念。

1.1.2 机器学习、深度学习能够做什么

机器学习应用场景非常多，可以说渗透到各行各业。医疗、航空、教育、物流、电商等等领域的各种场景。

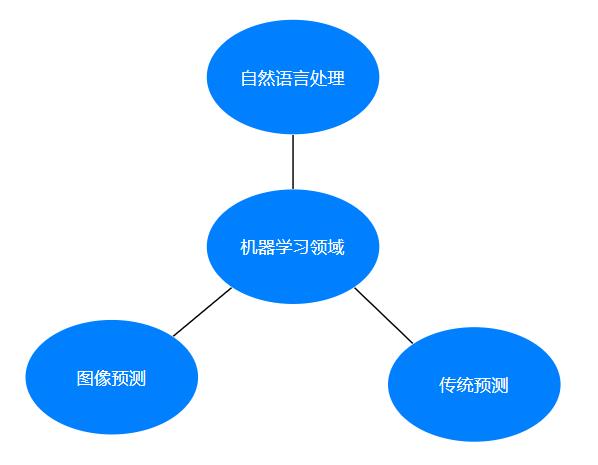
用在挖掘、预测领域：
- 应用场景：店铺销量预测、量化投资、广告推荐、企业用户分类…
用在图像领域：
- 应用场景：街道交通标志检测、人脸识别等等
用在自热语言处理领域：
- 应用场景：文本分类、情感分析、自动聊天、文本检测等等。

当前重要的是掌握一些机器学习算法等技巧，从某个行业切入解决问题。

1.2 什么是机器学习

1.2.1 定义

机器学习：是从数据中自动分析获得模型，并利用模型对未知数据进行预测。

1.2.2 数据集构成

结构：特征值+目标值

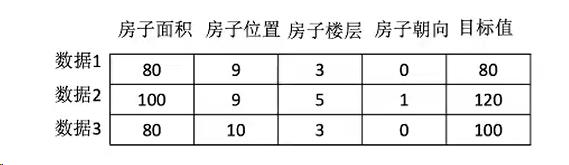
注释：

对于每一行数据我们称为样本。
有些数据可以没有目标值：

1.3 机器学习算法分类

1.3.1 监督学习

分类问题：有目标值，判断类别
回归问题：有目标值，连续型的数据

1.3.2 无监督学习

无监督学习：无目标值

1.4 机器学习开发流程

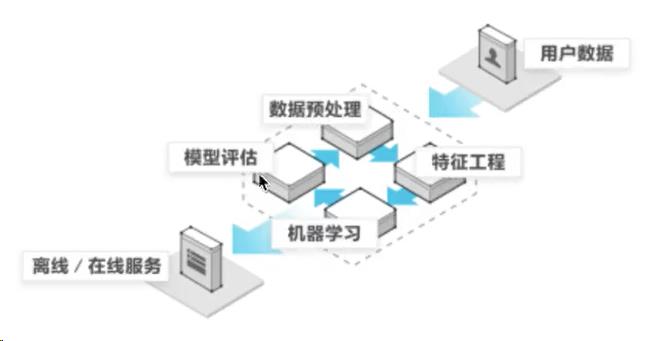
机器学习开发流程：

获取数据
数据处理
特征工程
机器学习算法训练 — 模型
模型评估
应用

1.5 学习框架和资料介绍

明确几点：

算法是核心，数据和计算是基础
找准定位

大部分的算法都有专有的算法工程师在做，而我们只要：

分析很多的数据
分析具体的业务
应用常见的算法
特征工程、调参数、优化

机器学习库和框架：

二特征工程

2.1 数据集

目标：
知道数据集分为训练集和测试集
会使用sklearn的数据集

应用：
无

2.1.1 可用数据集

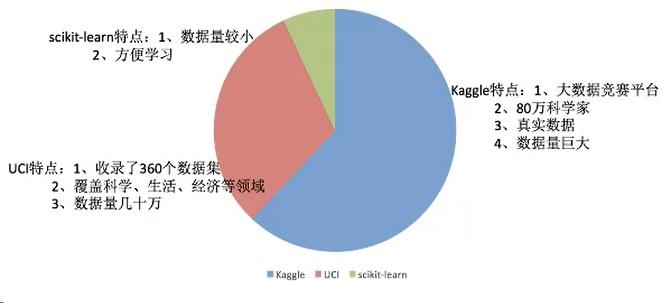
1、Scikit-learn工具介绍

Python语言的机器学习工具
Scikit-learn包括了许多知名的机器学习算法的实现
Scikit-learn文档完善，容易上手，丰富的API
最新稳定版本0.24

2、安装

conda install -c conda-forge scikit-learn

3、Scikit-learn包含的内容

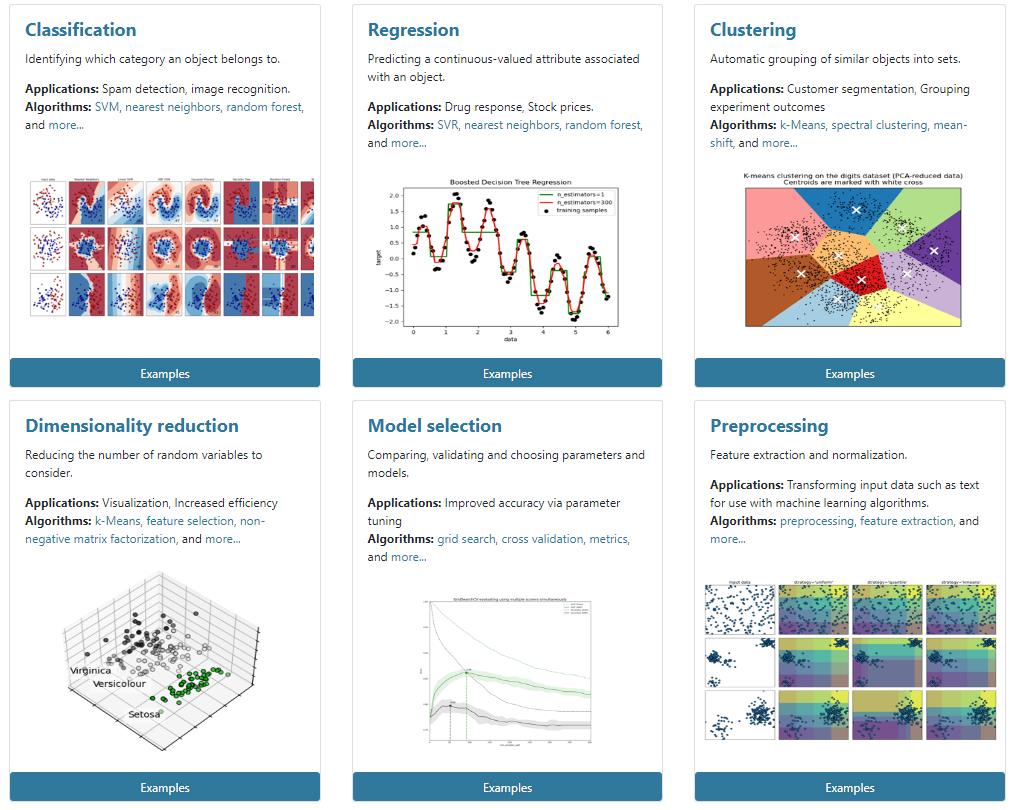
2.1.2 sklearn数据集

1、scikit-learn数据集API介绍

sklearn.datasets
- 加载获取流行的数据集
- datasets.load_*()
  - 获取小规模数据集，数据包含在datasets里
- datasets.fetch_*(data_home=None)
  - 获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录。

2、sklearn数据集返回

load和fetch返回的数据类型datasets.base.Bunch(字典格式)

def datasets_demo():
    """
    sklearn数据集使用
    :return:
    """
    # 获取数据
    iris = load_iris()
    print("鸢尾花数据集:\\n", iris)
    print("查看数据描述:\\n", iris["DESCR"])
    print("查看特征值的名字:\\n", iris.feature_names)
    print("查看特征值:\\n", iris.data, iris.data.shape)
    return None

2.1.3 数据集划分

机器学习一般的数据集会划分为两部分：【数据集结构：特征值和目标值】

训练数据：用于训练，构建模型
测试数据：在模型检验的时候使用，用于评估模型是否有效

划分比例：

训练集：70% 80% 90%
测试集：30% 20% 10%

数据集划分api

sklearn.model_selection.train_test_split(arrys,*options)

def datasets_demo():
    """
    sklearn数据集使用
    :return:
    """
    # 获取数据
    iris = load_iris()
    print("鸢尾花数据集:\\n", iris)
    print("查看数据描述:\\n", iris["DESCR"])
    print("查看特征值的名字:\\n", iris.feature_names)
    print("查看特征值:\\n", iris.data, iris.data.shape)

    # 数据集划分
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
    print("训练集的特征值：\\n", x_train, x_train.shape)
    return None

2.2 特征工程介绍

学习目标：

了解特征工程在机器学习中的重要性
知道特征工程的分类

2.2.1 为什么需要特征工程（Feature Engineering）

业界广泛流传：数据和特征决定了机器学习的上线，而模型和算法只是逼近这个上线而已。

2.2.2 什么是特征工程

特征工程是使用专业背景知识和技巧处理数据，使得特征能在机器学习算法上发挥更好的作用的过程。

意义：直接影响机器学习的效果

2.2.3 特征工程的位置与数据处理的比较

pandas：一个读取数据方便和基本处理数据格式的工具
sklearn：对于特征处理提供了强大的接口

2.3 特征抽取

目标：

应用DictVectorizer实现对类别特征进行数值化、离散化
应用CountVectorizer实现对文本特征进行数值化
应用TfidfVectorizer实现对文本特征进行数值化
区分两种文本特征提取的区别

2.3.1 特征提取

1、将任意数据（如文本或图像）转换成可用于机器学习的数字特征

注：特征值化是为了计算机更好的理解数据

字典特征提取（特征离散化）
文本特征提取
图像特征提取

2、特征提取API

sklearn.feature_extraction

2.3.2 字典特征提取

作用：对字典数据进行特征值化

sklearn.feature_extraction.DictVectorizer(…)

事例：

def dict_demo():
    """
    字典特征抽取
    :return:
    """
    data = ['city': "北京", 'temperature': 100, 'city': "上海", 'temperature': 60, 'city': "深圳", 'temperature': 30]
    # 1.实例化一个转换器
    # sparse 表示稀疏矩阵：只返回有值的位置，不返回0值
    transfer = DictVectorizer(sparse=False)
    # 2.调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("新数据:\\n", data_new)
    print("特征名字：\\n", transfer.get_feature_names())
    return None

执行结果：

2.3.3 文本特征提取

1、作用：对文本数据做特征值化

sklearn.feature_extraction.text.CountVectorizer(stop_words=[]) 返回词频矩阵
CountVectorizer.fit_transform(X) X：文本或者包含文本字符串的可迭代的对象，返回值sparse矩阵
CountVectorizer.inverse_transform(X) X:array数组或sparse矩阵返回值：转换前的数据格式
CountVectorizer.get_feature_names() 返回单词列表

def count_demo():
    """
    文本特征提取
    :return:
    """
    data = ["lift is short,i like like python", "lift is long,i dislike python"]
    # 1.实例化一个转换器
    transfer = CountVectorizer()
    # 2.调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("data_new:\\n", data_new.toarray())
    print("特征值列表：\\n", transfer.get_feature_names())
    return None

2、运行结果

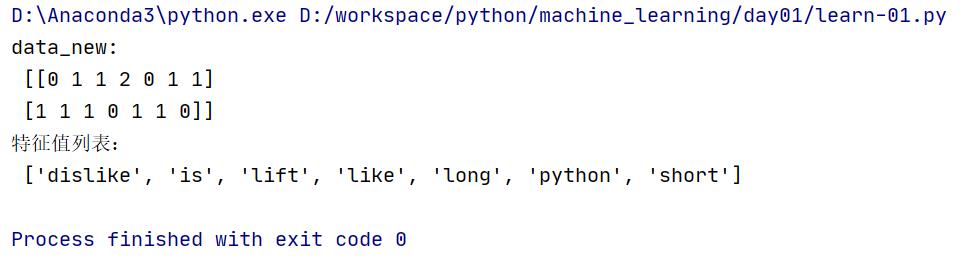
3、中文提取事例，注：因为中文词语之间没有空格分割，程序不能识别单个词，需要使用空格分割，之后会使用分词器，这里先手动分割验证。

def count_chinese_demo():
    """
    中文文本特征提取
    :return:
    """
    data = ["我 爱 北京 天安门", "天安门 上 太阳 升"]
    # 1.实例化一个转换器
    transfer = CountVectorizer()
    # 2.调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("data_new:\\n", data_new.toarray())
    print("特征值列表：\\n", transfer.get_feature_names())
    return None

4、中文提取：使用jieba分词器自动分词

def count_chinese_demo2():
    """
    中文文本特征提取,自动分词
    :return:
    """
    data = ["所谓的培训讲师，实则为一名感染新冠的个体营销职业人员。就是他，一个人传染了102个人，其中年龄最大的出生于1933年。",
            "发布会上，吉林省市场监管部门相关负责人表示，目前两地相关部门已经开展了联合调查，如有违法违规行为将进行严厉处罚。",
            "疫情防控大局当下，医护工作者仍然紧裹厚重的防护服，在前线与病毒奋勇厮杀，社区志愿者依旧冒寒风瑟瑟立于居民楼下“站岗守家”，可是竟有人在这个时候，举办“养生培训活动”推销产品，将老年人置于新冠病毒感染的“风口”，虽然打着关爱老年人健康的旗号，却无异于图财致命！"]
    # 分词
    data_new = []
    for item in data:
        data_new.append(" ".join(list(jieba.cut(item))))

    # 1.实例化一个转换器
    transfer = CountVectorizer(stop_words=["102", "1933", "一个"])
    # 2.调用fit_transform()
    data_final = transfer.fit_transform(data_new)
    print("data_new:\\n", data_final.toarray())
    print("特征值列表：\\n", transfer.get_feature_names())
    return None

运行结果：

引出问题：上诉方式进行对文章进行特征值抽取，某词语出现次数很多，单是在其他文章出现次数很少

解决方法：使用 TfidfVectorizer

5、Tf-idf 文本特征提取

TF-IDF的主要思想：如果某个词或者短语在一片文章中出现的概率很高，并且在其他文章中很少出现，则认为此词语或短语有很好的类别区分能力，适合用作分类。
TF-IDF：用以评估一个词语对一个文件集或一个语料库中的其中一份文件的重要程度。
TF：词频（term frequency）
IDF：逆向文档频率
API：sklearn.feature_extraction.text.TfidfVectorizer()

案例：

def tfidf_demo():
    """
    使用TF-IDF对中文文本特征提取,自动分词
    :return:
    """
    data = ["所谓的培训讲师，实则为一名感染新冠的个体营销职业人员。就是他，一个人传染了102个人，其中年龄最大的出生于1933年。",
            "发布会上，吉林省市场监管部门相关负责人表示，目前两地相关部门已经开展了联合调查，如有违法违规行为将进行严厉处罚。",
            "疫情防控大局当下，医护工作者仍然紧裹厚重的防护服，在前线与病毒奋勇厮杀，社区志愿者依旧冒寒风瑟瑟立于居民楼下“站岗守家”，可是竟有人在这个时候，举办“养生培训活动”推销产品，将老年人置于新冠病毒感染的“风口”，虽然打着关爱老年人健康的旗号，却无异于图财致命！"]
    # 分词
    data_new = []
    for item in data:
        data_new.append(" ".join(list(jieba.cut(item))))

    # 1.实例化一个转换器
    transfer = TfidfVectorizer(stop_words=["102", "1933", "一个"])
    # 2.调用fit_transform()
    data_final = transfer.fit_transform(data_new)
    print("data_new:\\n", data_final.toarray())
    print("特征值列表：\\n", transfer.get_feature_names())
    return None

运行结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B5oG3ZOI-1639485950300)(https://juejin.cn/)]

2.4 特征预处理

目标：

了解数值型数据、类别型数据特点
应用MinMaxScaler实现对特征数据进行归一化
应用StandardScaler实现对特征数据进行标准化

2.4.1 概要

什么是特征预处理：

通过一些转换函数将特征数据转化为更加适合算法模型的特征数据过程

1、包含内容

归一化
标准化

2、特征预处理API

sklearn.preprocessing

为什么我们需要归一化？

特征的单位或者大小相差较大，或者某特征的方差比其他特征的方差大出几个数量级，容易影响（支配）目标结果，使得一些算法无法学习到其它的特征。

2.4.2 归一化

1、定义：通过对原始数据的转换，把3数据映射到（默认值[0,1]）之间

2、公式

def minmax_demo():
    """
    归一化
    :return:
    """
    # 1.获取数据
    data = pd.read_csv('../data/dating.csv', encoding="gbk")
    data = data.iloc[:, 0:8]
    # 2.实例化一个转换器
    transfer = MinMaxScaler()
    # 3.调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\\n", data_new)
    # 4.

    return None

结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eCgsTLrP-1639485950302)(https://juejin.cn/)]

总结：存在异常值时，即最大值或最小值为异常值的情况，归一化值是不准确的，只适合传统精确小数据场景。

2.4.3 标准化

1、定义：通过对原始数据进行变换，把数据变换到均值为0，标准差为1的范围内

2、公式

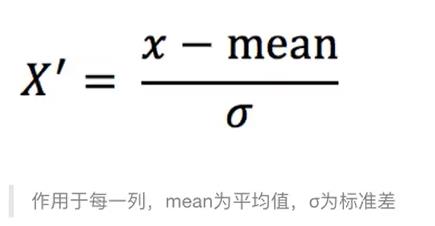
对于归一化来说：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变
对于标准化来说：如果出现异常点，由于具有一定的数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小。

3、API

sklearn.preprocessing.StandardScaler()

4、数据计算

同样对上面的数据进行处理

分析

实例化StandardScaler
通过fit_transform转换

def stand_demo():
    """
    标准化
    :return:
    """
    # 1.获取数据
    data = pd.read_csv('../data/dating.csv', encoding="gbk")
    data = data.iloc[:, 0:8]
    # 2.实例化一个转换器
    transfer = StandardScaler()
    # 3.调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\\n", data_new)
    return None

执行结果：

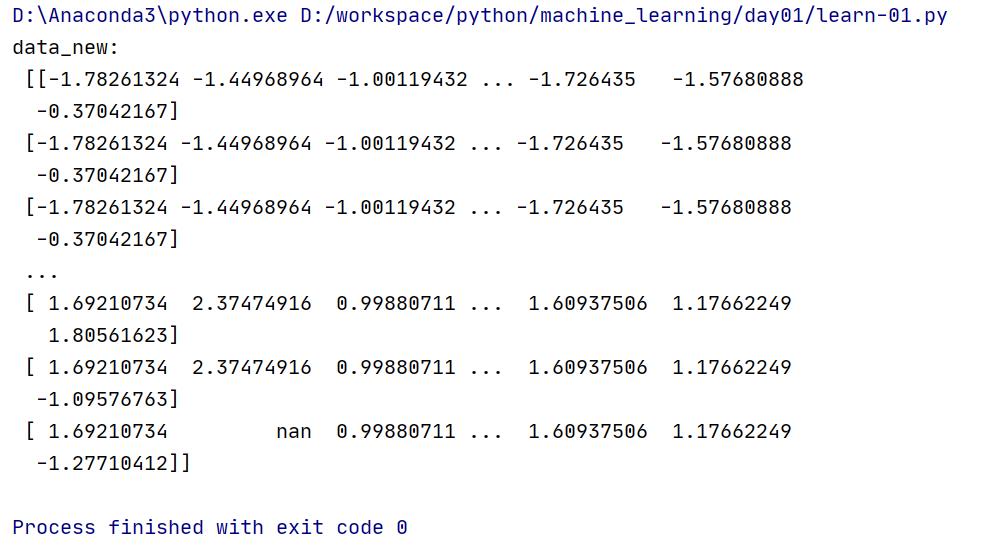
总结：

标准差：集中程度

在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

2.5 特征降维

目标：

应用 VarianceThreshold实现删除低方差特征
了解相关系数特点和计算
应用相关系数实现特征值选择

2.5.1 降维

降维：指在某些限定条件下，降低随机变量（特征）个数，得到一组“不相关” 主变量的过程

降低随机变量的个数

相关特征
- 相对湿度与降雨量之间的相关
- …

正因为在进行训练的时候，我们都是使用特征值进行学习的。如果特征本身存在问题或者特征之间相关性较强，对于算法学习预测会影响较大。

2.5.2 降维的两种方式

特征选择
主成分分析（可以理解一种特征提取的方式）

2.5.3 什么是特征选择

1、定义：数据中包含冗余或者相关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。

2、方法

Filter(过滤式)：主要探究特征本身的特点，特征与特征和目标值之间关联
- 方差选择法：低方差过滤
- 相关系数
Embedded(嵌入式)：算法自动选择特征（特征与目标值之间的关联）
- 决策树：信息熵、信息增益
- 正则化：L1、L2
- 深度学习：卷积等

3、模块

sklearn.feature_selection

4、过滤式

4.1 低方差特征过滤

删除地方差的一些特征：

特征方差小：某个特征大多样本的值比较相近
特征方差大：某个特征很多样本的值都有差别

sklearn.feature_selection.VarianceThreshold(threshold=0.0)
删除所有低方差特征
Variance.fit_transform(X)
X：numpy array格式的数据[n_samples,n_features]
返回值：训练值低于 threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

def variance_demo():
    """
    过滤低方差特征
    :return:
    """
    # 1.获取数据
    data = pd.read_csv('../data/dating.csv', encoding="gbk")
    data = data.iloc[:, 1:8]
    # 2.实例化一个转换器
    transfer = VarianceThreshold(threshold=10)
    # 3.调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\\n", data_new, data_new.shape)

    # 计算两个变量之间的相关系数
    r = pearsonr(data["gender"], data["position"])
    print("相关系统：\\n", r)
    return None

执行结果：

4.2 相关系数

皮尔逊相关系数
- 反映变量之间相关关系密切程度的统计指标

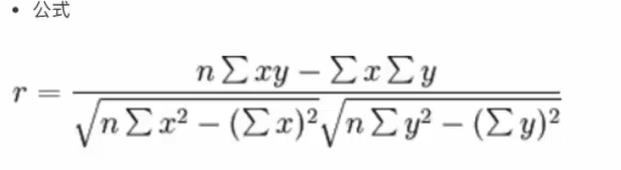
相关系数的值介于-1与+1之间，即[-1,+1]

当r大于0时，表示两个变量正相关，r小于零时，两个变量负相关
当r绝对值等于1时，表示两个变量为完全相关，当r=0时，表示两个变量无相关关系
当0<|r|<1时，表示两个变量存在一定程度的相关。且|r|越接近1，两个变量之间的线性关系越密切；|r|越接近0时，两个变量线性相关越弱。
一般可按三级划分：|r|<0.4 为低度相关；0.4<=|r|<0.7 为显著相关； 0.7<=|r|<1 为高度线性相关。

from scipy.stats import pearsonr

2.6 主成分分析

目标：

应用PCA实现特征的降维

应用：

用户和物品类别之间主成分分析

2.6.1 简介

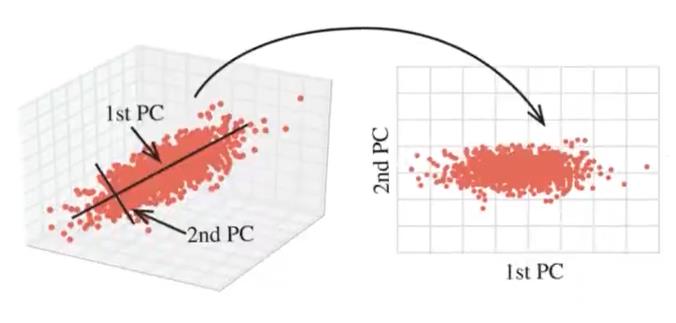
主成分分析（PCA）：高维数据转化为低维数据的过程，此过程中可能会舍弃原有数据、创造新的变量。

作用：是数据维数压缩，尽可能降低原始数据的维数（复杂度），损失少量信息。

应用：回归分析或者聚类分析当中。

API：

sklearn.decomposition.PCA(n_components=None)

def pca_demo():
    """
    PCA降维
    :return:
    """
    # 准备数据
    data = [[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]
    # 实例化转换器
    transfer = PCA(n_components=0.95)
    # 调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("data_new:\\n", data_new)
    return None

执行结果：

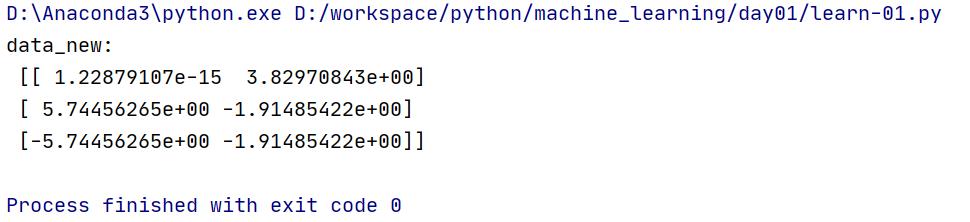
2.6.2 案例

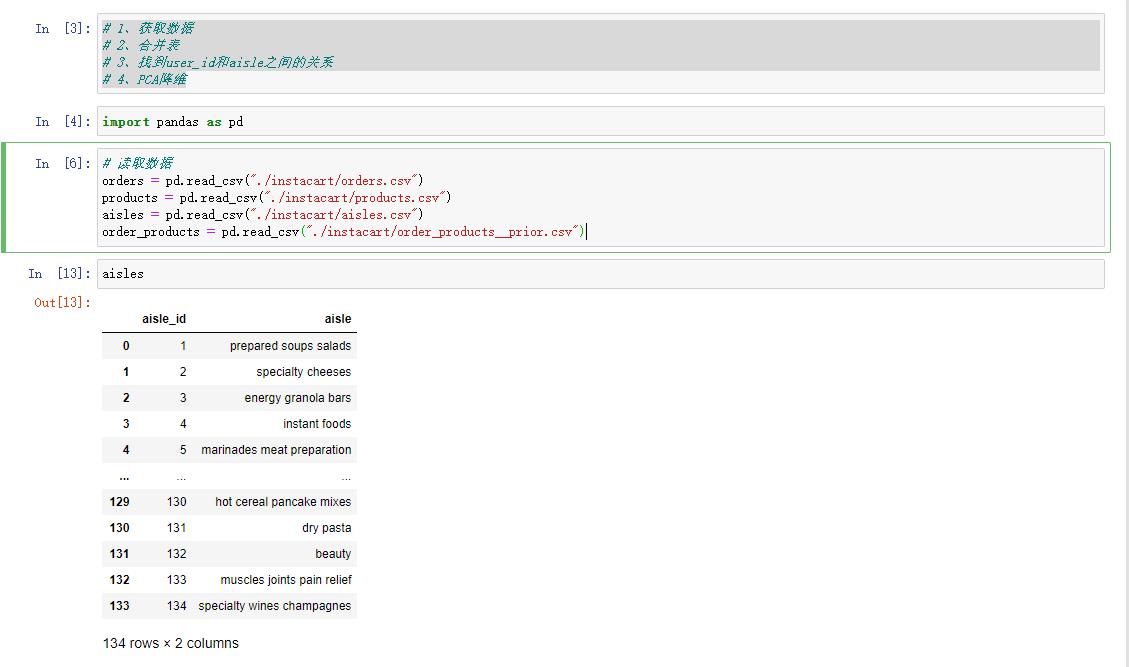
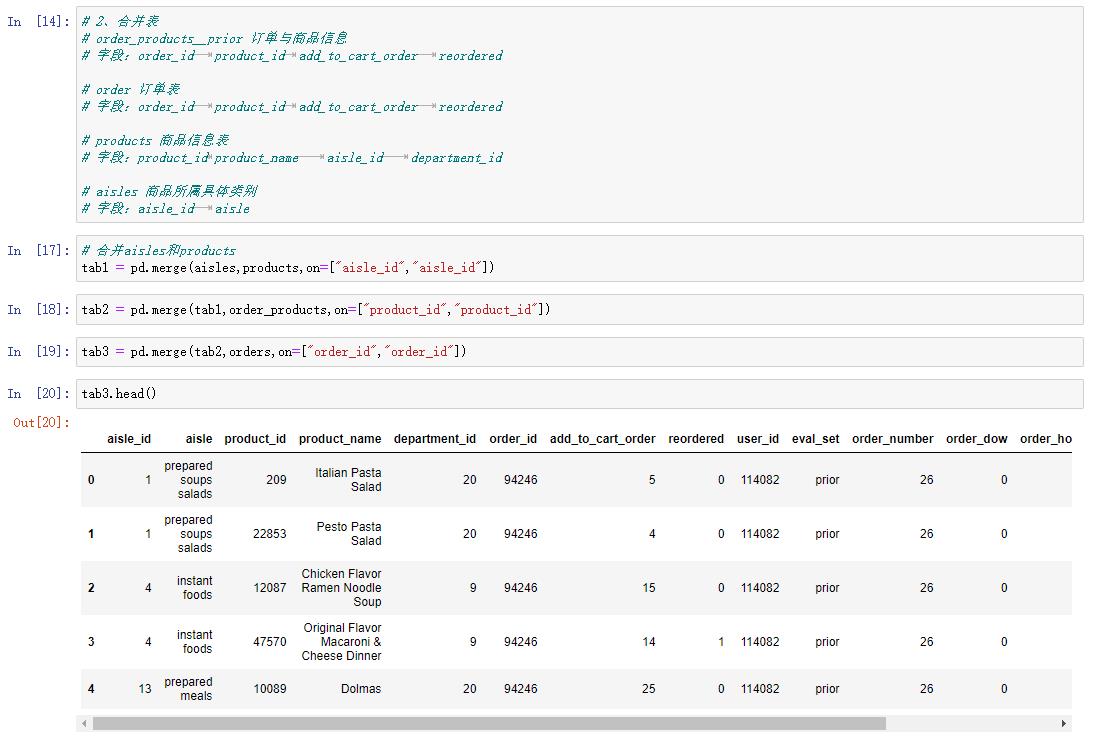
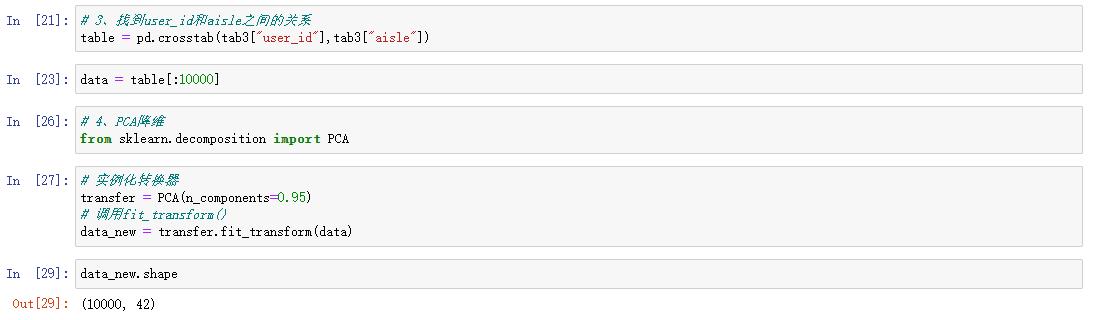
探索用户对物品类别的喜好细分

# 运行jupyter notebook
jupyter notebook

三分类算法

3.1 sklearn转换器和估计器

目标

知道sklearn的转换器和估计器流程

3.1.1 转换器

特征工程的步骤：

实例化（实例化的是一个转换器类（Transformer））
调用fit_transform(对于文档建立类词频矩阵，不能同时调用)

我们把特征的接口称之为转换器，其中转换器有这么几种形式：

fit_transform
fit
transform

例如，标准化：

(x - mean)/ std

fit_transform

fit 计算每一列的平均值、标准差

transform (x - mean)/ std进行最终的转换

3.1.2 估计器

在sklearn中，估计器（estimator）是一个重要的角色，是一类实现算法的api

用于分类的估计器
sklearn.neighbors k-近邻算法
sklearn.native_bayes 贝叶斯
sklearn.linear_model.LogisticRegression 逻辑回归
sklearn.tree 决策树与随机森林

用于回归的估计器：
sklearn.linear_model.LinearRegression 线性回归
sklearn.linear_model.Ridge 岭回归

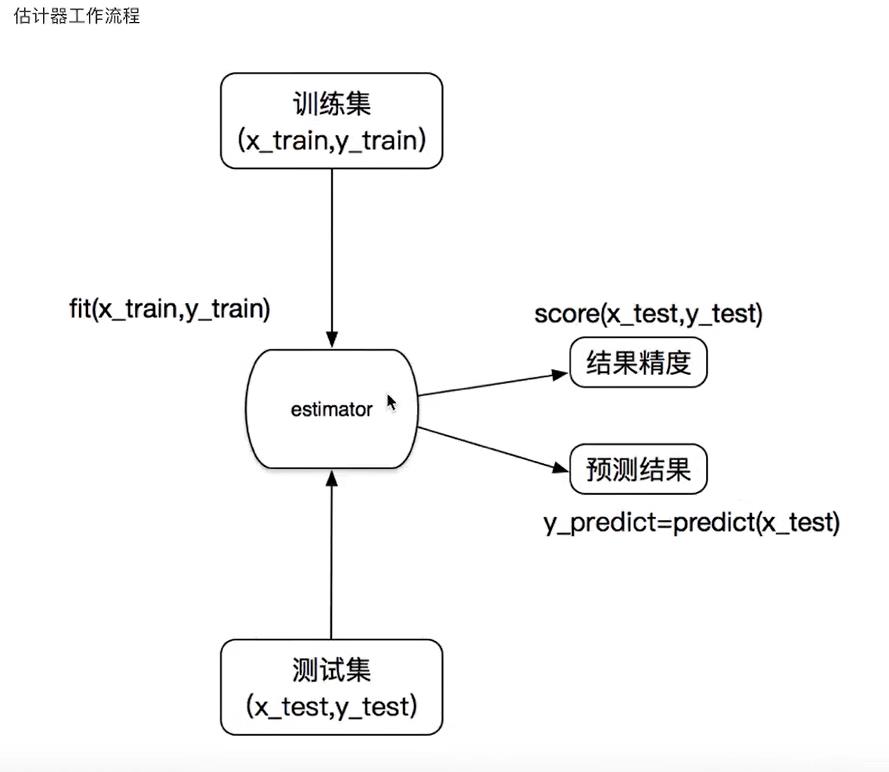
3.2 K-近邻算法

学习目标

学习KNN算法的距离公式
学习KNN算法的超参数K值以及取值问题
学习KNN的优缺点
应用KNeighborsClassifier实现分类
了解分类算法的评估标准准确率

1、K-近邻算法（KNN）原理

K Nearest Neighbor 算法又叫KNN算法

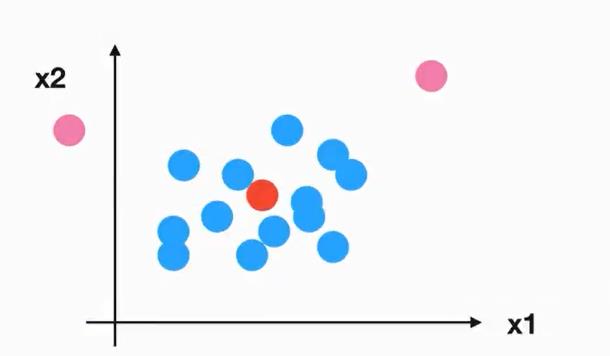
定义：如果一个样本在特征空间中的k个最相近（即特征空间中最近邻）的样本中的大多数属于某一个类别，则这个样本属于这个类别。

两个样本的距离，又叫欧式距离

用KNN算法对鸢尾花进行分类

def knn_iris():
    """
    用KNN算法对鸢尾花进行分类
    :return:
    """
    # 1、获取数据
    iris = load_iris()
    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)
    # 3、特征工程：标准化
    tranfer = StandardScaler()
    x_train = tranfer.fit_transform(x_train)
    x_test = tranfer.fit_transform(x_test)
    # 4、KNN算法预估值器
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)
    # 5、模型评估
    # 方法一：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\\n", y_predict)
    print("直接对比真实值和预测值：\\n", y_predict == y_test)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\\n", score)
    return None

运行结果：

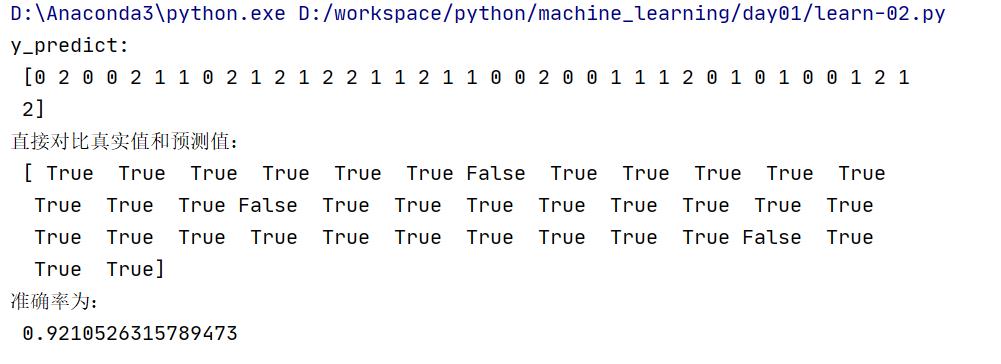
3.3 模型选中与调优

学习目标：

交叉验证过程
超参数搜索过程
应用GridSearchCV实现算法参数的调优

3.3.1 交叉验证

交叉验证：将拿到的训练数据，分为训练和验证集。以下图为例：将数据分为4份，其中一份作为验证集。然后经过4次的测试，每次都要更换不同的验证集。即得到4组模型结果，取平均值作为最终结果。又称为4折交叉验证。

数据分为训练集和测试集，但为了让从训练集得到的模型结果更加准确，所以做以下处理：

用KNN算法对鸢尾花进行分类，添加网络搜索和交叉验证

def knn_iris_gscv():
    """
    用KNN算法对鸢尾花进行分类，添加网络搜索和交叉验证
    :return:
    """
    # 1、获取数据
    iris = load_iris()
    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)
    # 3、特征工程：标准化
    tranfer = StandardScaler()
    x_train = tranfer.fit_transform(x_train)
    x_test = tranfer.fit_transform(x_test)
    # 4、KNN算法预估值器
    estimator = KNeighborsClassifier()

    # 加入网络搜索和交叉验证
    # 参数准备
    param_dict = "n_neighbors": [1, 3, 5, 7, 9, 11]
    estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)

    estimator.fit(x_train, y_train)
    # 5、模型评估
    # 方法一：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\\n", y_predict)
    print("直接对比真实值和预测值：\\n", y_predict == y_test)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\\n", score)

    # 最佳参数
    print("最佳参数:\\n", estimator.best_params_)
    # 最佳结果
    print("最佳结果:\\n", estimator.best_score_)
    # 最佳估计器
    print("最佳估计器:\\n", estimator.best_estimator_)
    # 交叉验证结果
    print("交叉验证结果:\\n", estimator.cv_results_)

    return None

运行结果：

Facebook案例

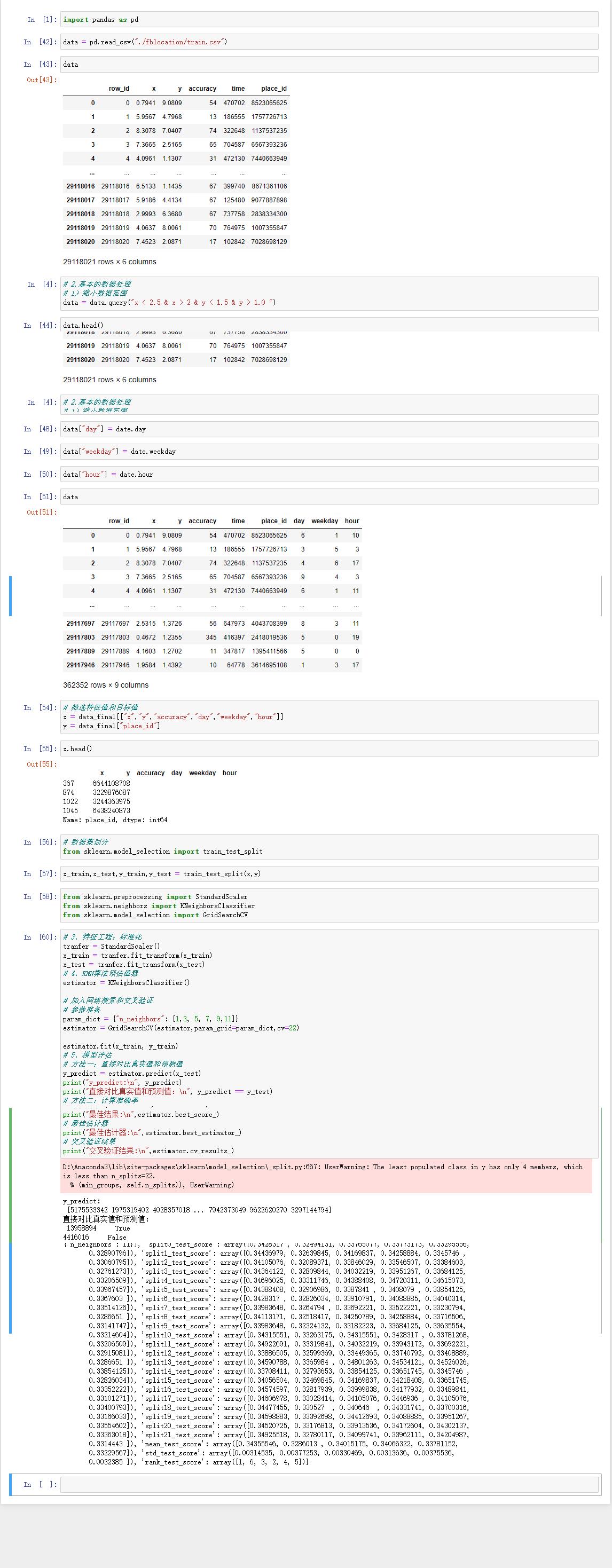
3.4 朴素贝叶斯算法

学习目标：

条件概率与联合概率
贝叶斯公式，以及特征独立的关系
拉普拉斯平滑系数
应用贝叶斯公式实现概率的计算

3.4.1 什么是朴素贝叶斯分类方法

根据朴素贝叶斯算法分类后能够出现以下的概率值，通过概率值的大小把邮件分类

3.4.2 概率基础

1、概率（Probability）定义

概率定义为一件事情发生的可能性
P(X)：取值在[0,1]

3.4.3 联合概率、条件概率与相互独立

联合概率：包含多个条件，且所有条件同时成立概率
记作：P(A,B)

条件概率：事件A在事件B发生条件下的发生概率
记作：P(A|B)

相互独立：如果P(A,B) = P(A)P(B),则称为事件A与事件B相互独立
P(A,B) = P(A)P(B) <=> 事件A与事件B相互独立

3.4.4 贝叶斯公式

3.4.5 API

sklearn.naive_bayes.MultinomiaINB(alpha = 1.0)
朴素贝叶斯分类
alpha ：拉普拉斯平滑系数

3.4.6 案例

def nb_news():
    """
    用朴素贝叶斯算法对新闻进行分类
    :return:
    """
    # 获取数据
    news = fetch_20newsgroups(subset="all")
    # 划分数据集:特征训练集，特征测试集，目标训练集，目标测试集
    x_train,x_test,y_train,y_test = train_test_split(news.data,news.target)
    # 特征工程:文本特征抽取tfidf
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train,y_train)
    # 模型评估
    # 方法一：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\\n", y_predict)
    print("直接对比真实值和预测值：\\n", y_predict == y_test)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\\n", score)
    return None

运行结果：

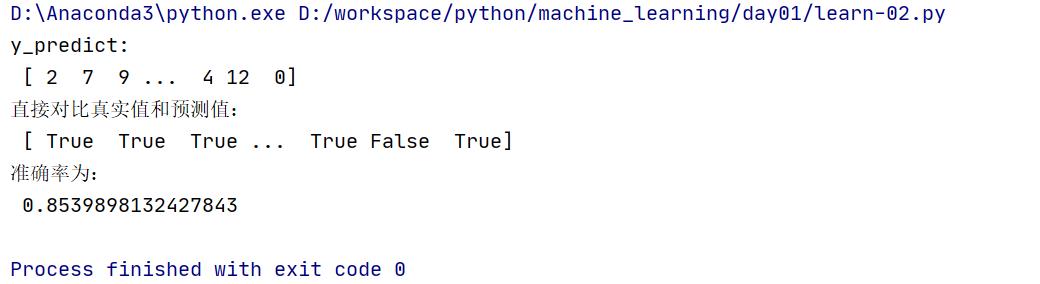
3.5 决策树

学习目标：

信息熵的公式以及作用
信息的公式和作用
应用信息增益的实现计算特征的不确定性减少程度
了解决策树三种算法实现

3.5.1 认识决策树

决策树的思想非常朴素，程序设计中的条件分支结构就是if-else结构，最早的决策树就是利用这种结构分割数据的一种分类学习方法

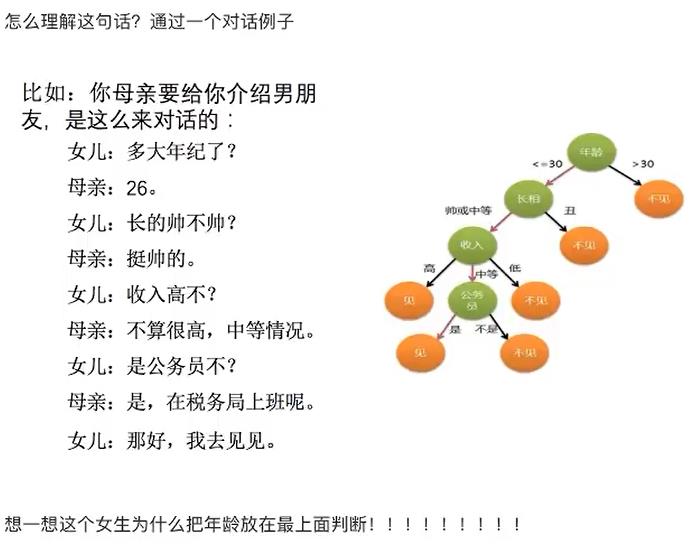
3.5.2 决策树原理

1、原理

信息熵，信息增益

2、信息熵的定义

H的专业术语称之为信息熵，单位为比特

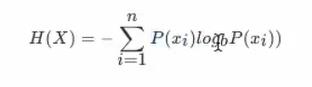
3、决策树划分依据之一-----信息熵

定义：特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即：

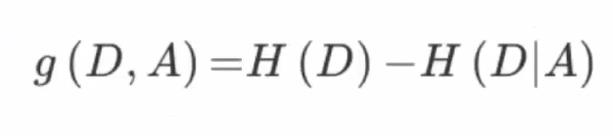
3.5.4 案例

1、用决策树对鸢尾花进行分类

def decision_iris():
    """
    用决策树对鸢尾花进行分类
    :return:
    """
    # 1、获取数据集
    iris = load_iris()
    # 2、划分数据集
    x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=22)
    # 3、决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train,y_train)
    # 4、模型评估
    # 方法一：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\\n", y_predict)
    print("直接对比真实值和预测值：\\n", y_predict == y_test)
    # 方法二：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\\n", score)

    # 可视化决策树
    export_graphviz(estimator,out_file="iris_tree.dot")
    return None

运行结果：

2、泰坦尼克号乘客生存预测

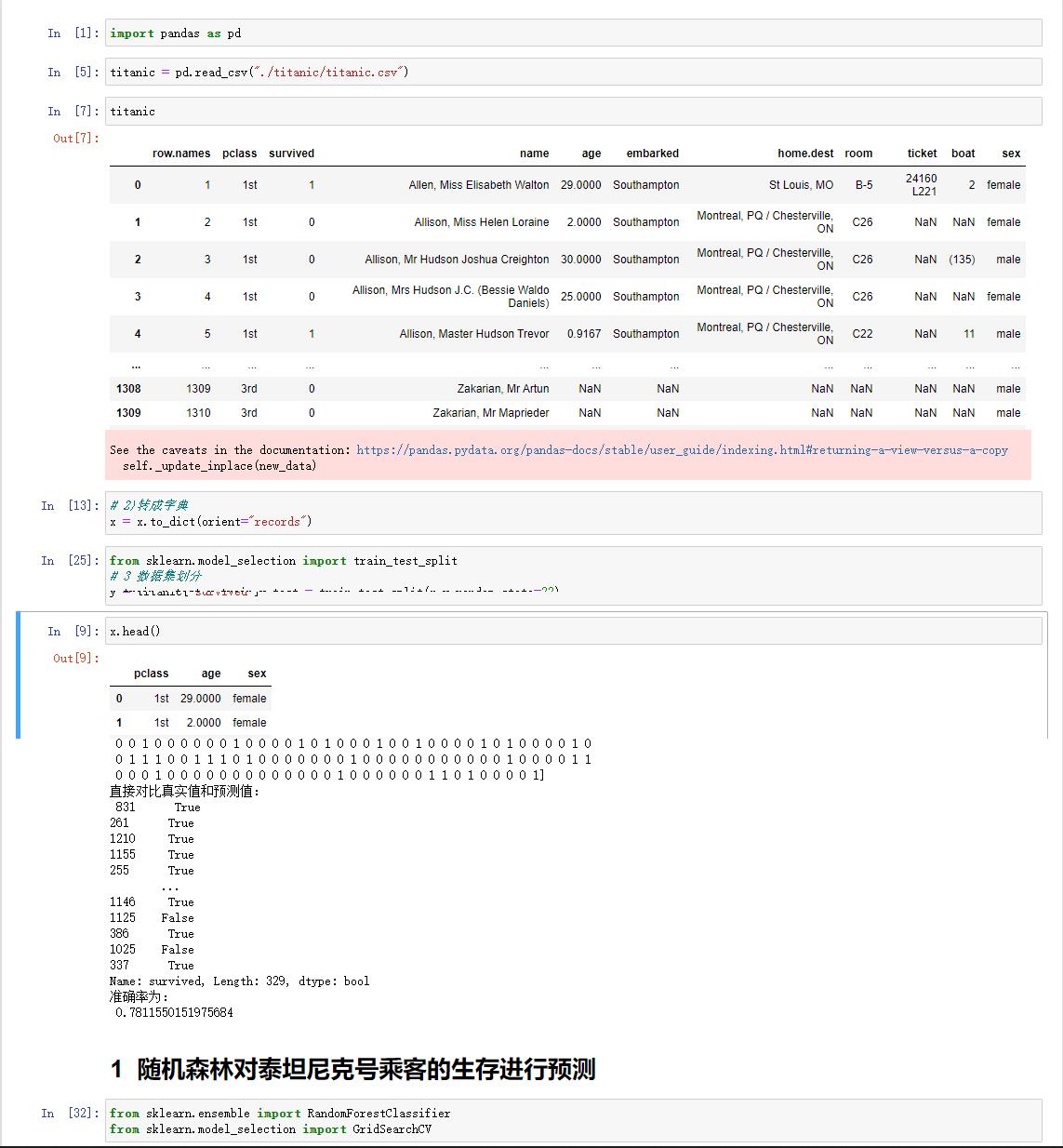
3.5.6 决策树总结

优点：
简单的理解和解释，树木可视化

缺点：
决策树创建者可以创建，但是不能很好的推广数据过于复杂的树，这被称为过拟合

改进：
减枝cart算法（决策树API当中已经实现）
随机森林

3.6 集成学习方法之随机森林

学习目标：

随机森林每一颗决策树的建立过程
为什么需要随机有放回（Bootstrap）的抽样
随机森林的超参数

3.6.1 什么集成学习方法

集成学习是通过建立几个模型组合的来解决单一预测问题。

它的工作原理是生成多个分类器/模型，各自独立地学习和做出预测。这些预测最后结合成组合预测，因此由于任何一个单分类的做出预测。

3.6.2 什么是随即森林

随机森林是包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

3.6.3 随机森林原理过程

学习算法根据下列算法创建每课树：

用N来表示训练用例的个数，M表示特征数目。
一次随机选出一个样本，重复N次（有可能出现重复样本）
随机去选择m个特征，m<<M ,建立决策树

采取bootstrap抽样

3.6.4 API

3.6.5 案例

泰坦尼克号乘客生存预测

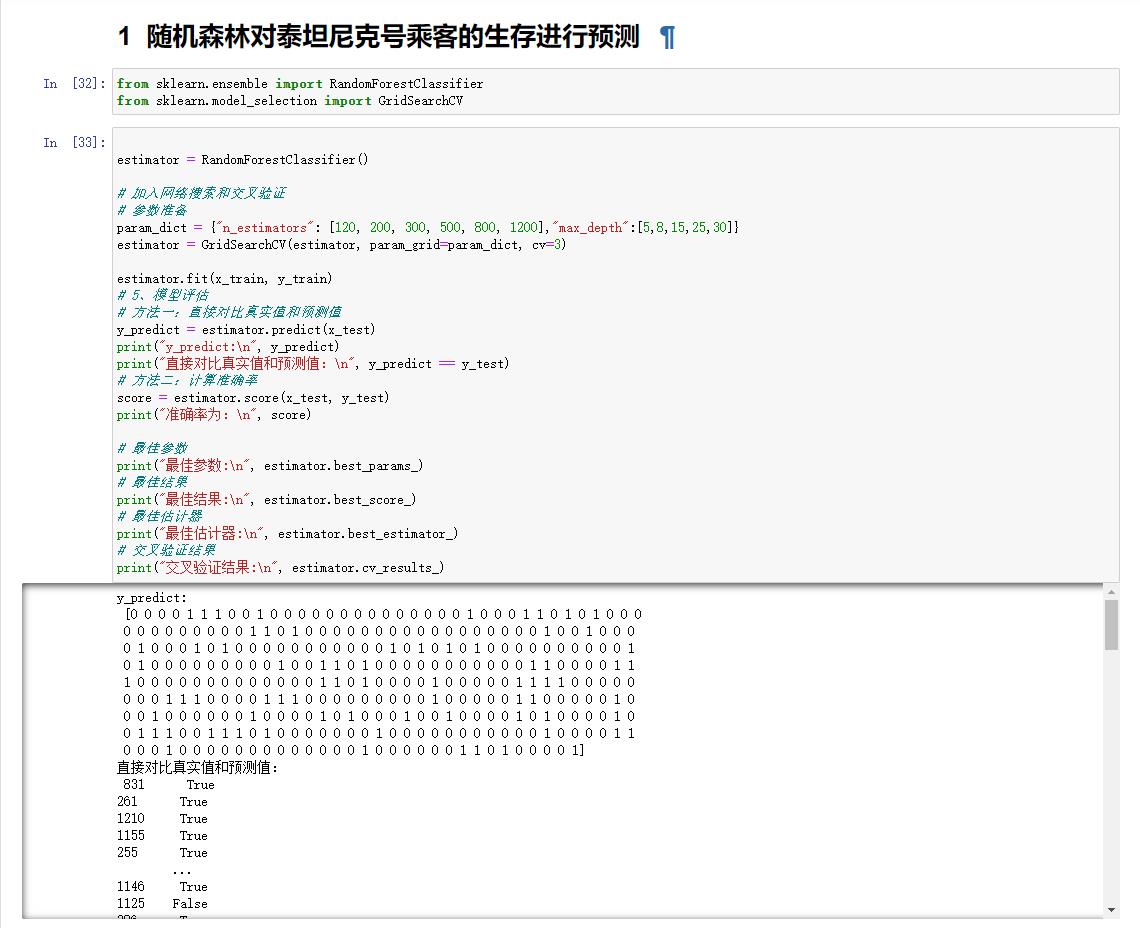
四回归与聚类算法

4.1 线性回归

学习目标：

线性回归的原理过程
应用LinearRegression或SGDRegressor实现回归预测
回归算法的评估标准及其公式

4.1.1 线性回归的原理

1、线性回归的应用场景

2、什么事线性回归

定义与公式

4.1.2 线性回归的损失和优化原理

1、损失函数：也称为cost、成本函数、目标函数

2、优化方法

正规方程：使用比较少

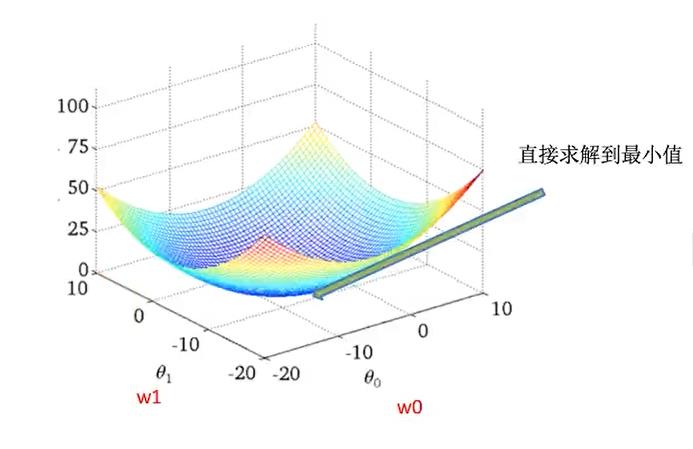
梯度下降（Gradient Descent）

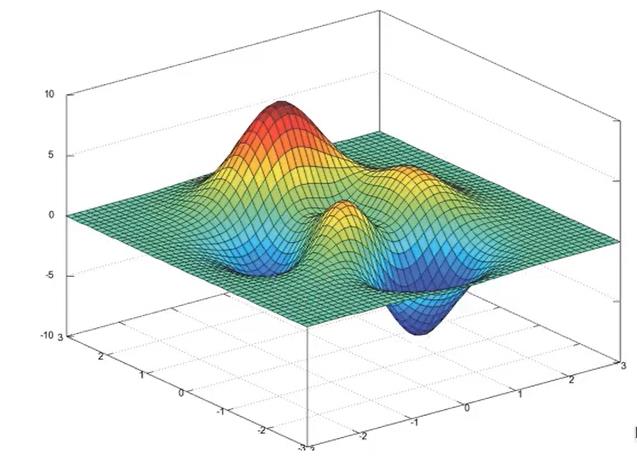
案例：

def linear1():
    """
    正规方程的优化方法对波斯顿房价进行预测
    :return:
    """
    # 1、获取数据
    boston = load_boston()
    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
    # 3、标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4、预估器
    estimator = LinearRegression()
    estimator.fit(x_train,y_train)

    # 5、得出模型
    print("正规方程-权重系数：\\n",estimator.coef_)
    print("正规方程-偏置为:\\n",estimator.intercept_)

    # 6、模型评估
    return None

def linear2():    """    梯度下降的优化方法对波斯顿房价进行预测    :return:    """    # 1、获取数据    boston = load_boston()    # 2、划分数据集    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)    # 3、标准化    transfer = StandardScaler()    x_train = transfer.fit_transform(x_train)    x_test = transfer.transform(x_test)    # 4、预估器    estimator = SGDRegressor()    estimator.fit(x_train, y_train)    # 5、得出模型    print("梯度下降-权重系数：\\n", estimator.coef_)    print("梯度下降-偏置为:\\n", estimator.intercept_)    # 6、模型评估    return None

运行结果：

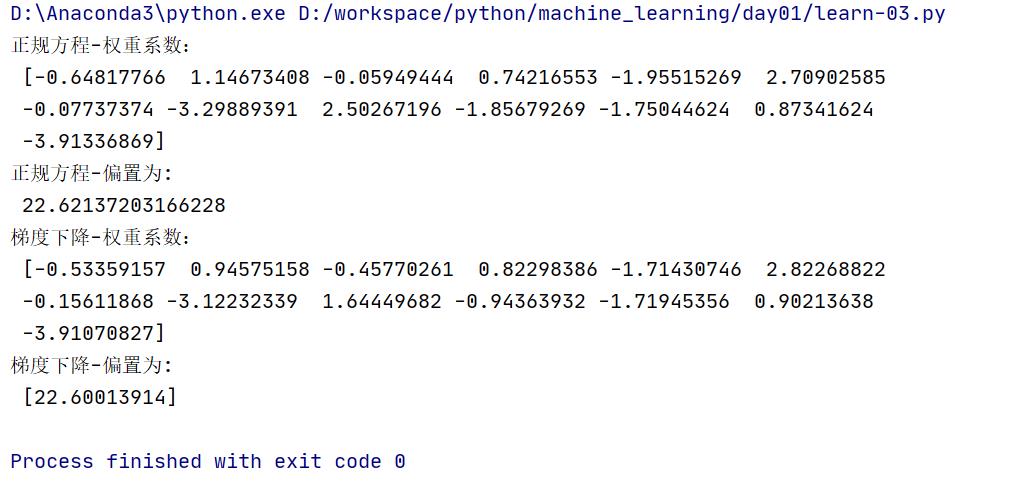
4.1.3 回归性能评估

from sklearn.metrics import mean_squared_error

def linear1():
    """
    正规方程的优化方法对波斯顿房价进行预测
    :return:
    """
    # 1、获取数据
    boston = load_boston()
    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
    # 3、标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4、预估器
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    # 5、得出模型
    print("正规方程-权重系数：\\n", estimator.coef_)
    print("正规方程-偏置为:\\n", estimator.intercept_)

    # 6、模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价:\\n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("正规方程-均方误差为：\\n", error)

    return None

def linear2():    """    梯度下降的优化方法对波斯顿房价进行预测    :return:    """    # 1、获取数据    boston = load_boston()    # 2、划分数据集    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)    # 3、标准化    transfer = StandardScaler()    x_train = transfer.fit_transform(x_train)    x_test = transfer.transform(x_test)    # 4、预估器    estimator = SGDRegressor()    estimator.fit(x_train, y_train)    # 5、得出模型    print("梯度下降-权重系数：\\n", estimator.coef_)    print("梯度下降-偏置为:\\n", estimator.intercept_)    # 6、模型评估    y_predict = estimator.predict(x_test)    print("预测房价:\\n", y_predict)    error = mean_squared_error(y_test, y_predict)    print("梯度下降-均方误差为：\\n", error)    return None

4.1.4 正规方程和梯度下降对比

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大时可以使用	需要计算方程，时间复杂度高O(n3)

选择
- 小规模数据：
  - LinearRegression（不能解决拟合问题）
  - 岭回归
- 大规模数据：SGDRegressor

4.1.5 扩展

优化方法：GD、SGD、SAG

1、GD

梯度下降（Gradient Descent），原始的梯度下降需要计算所有的值才能得到梯度，计算量大，所以才有改进算法。

2、SGD

随机梯度下降（Stochastic gradient descent）:她在一次迭代时只考虑一个训练样本。

SGD的有点：
高效
容易实现

SGD的缺点：
SGD需要许多超参数：比如正则项参数，迭代数。
SGD对于特征标准化是敏感的

3、SAG

随机平均梯度下降（Stochastic Average gradient），由于收敛的速度太慢，有人提出了SAG等基于梯度下降的算法。

岭回归、逻辑回归等当中都有SAG优化

4.2 欠拟合和过拟合

学习目标：

线性回归（不带正则化）的缺点
过拟合和欠拟合的原因和解决方法

4.2.1 简介

1、欠拟合

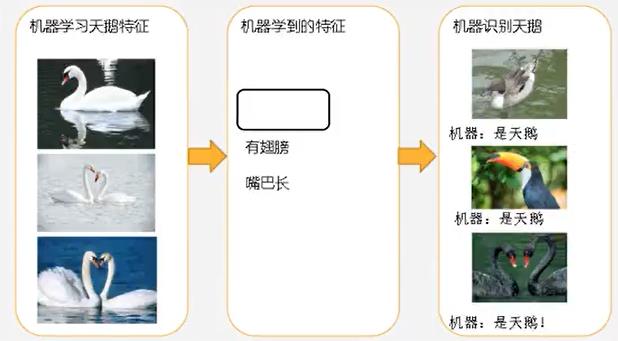
2、过拟合

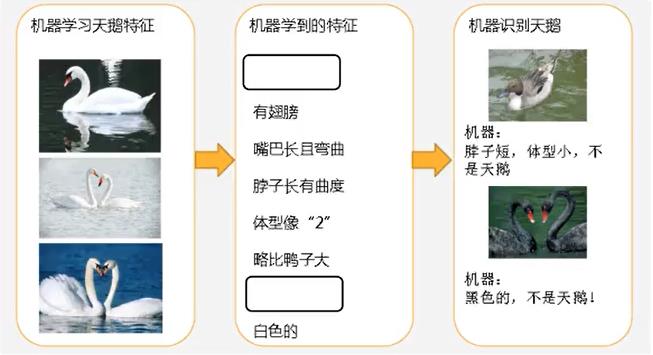
分析：

第一种情况：因为机器学习的天鹅特征太少了，导致区分标准太粗糙，不能准确识别天鹅
第二种情况：机器基本能区分天鹅了。然而，很不巧已有的天鹅图片全是白天鹅，然后机器学习后，认为天鹅的羽毛是白色的，以后看到羽毛是黑色的天鹅就认为那不是天鹅。

过拟合：一个假设在训练集上能够获得比其他假设更好的拟合，但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合现象。（模型过于复杂）
欠拟合：一个假设在训练集数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。（模型过于简单）

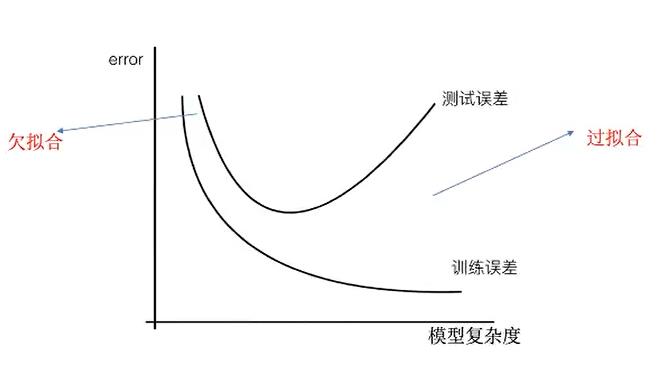
4.2.2 原因和解决方法

欠拟合原因以及解决方法
原因：学习到数据的特征太少
解决方法：增加数据的特征数量

过拟合原因以及解决办法
原因：原始特征太多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试点的数据
解决方法：
正则化

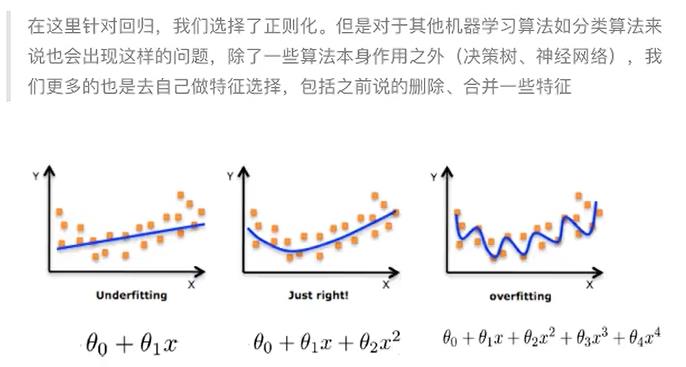
正则化：L2正则化（常用）、L1正则化

4.3 线性回归的改进—岭回归

学习目标：

学习岭回归的原理与线性回归的不同之处
正则化对于权重参数的影响
L1和L2正则化的区别

4.3.1 带有L2正则化的线性回归—岭回归

岭回归其实也是一种线性回归。只不过在算法建立回归方程时，加上正则化的限制，从而达到解决过拟合的效果。

1、API

2、观察正则化程度的变化，对结果的影响

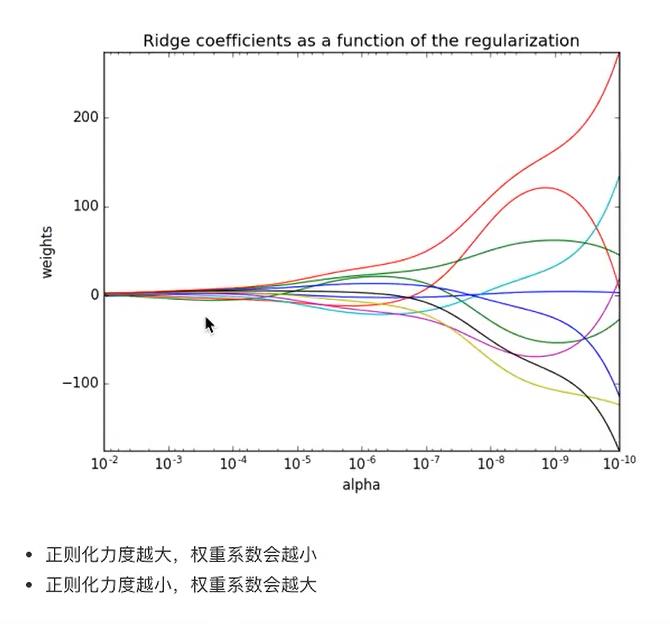
案例：岭回归对波斯顿房价进行预测

def linear3():
    """
    岭回归对波斯顿房价进行预测
    :return:
    """
    # 1、获取数据
    boston = load_boston()
    # 2、划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
    # 3、标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4、预估器
    estimator = Ridge(alpha=0.5, max_iter=10000)
    estimator.fit(x_train, y_train)

    # 5、得出模型
    print("岭回归-权重系数：\\n", estimator.coef_)
    print("岭回归-偏置为:\\n", estimator.intercept_)

    # 6、模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价:\\n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("岭回归-均方误差为：\\n", error)
    return None

4.4 分类算法—逻辑回归与二分类

学习目标：

逻辑回归的损失函数
逻辑回归的优化方法
sigmoid函数
逻辑回归的应用场景
精确率、召回率指标的区别
F1-score指标，召回率的实际意义
如何解决样本不均衡情况下的评估
ROC曲线的意义，AUC指标大小
应用classification_report实现精确率、召回率计算
应用roc_auc_score实现指标计算

4.4.1 逻辑回归

定义：逻辑回归（Logistic Regression）是机器学习的一种分类模型，逻辑回归是一种分类算法，虽然名字中带有回归，但是它与回归之间有一定的联系。由于算法的简单与高效，在实际中应用非常广泛。

应用场景：

广告点击率
是否为垃圾邮件
是否患病
金融诈骗
虚假账号

注意： 看见上面的例子，我们会发现其中的特点，那就是属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器。

4.4.2 逻辑回归原理

1、输入：线性回归的输出就是逻辑回归的输入

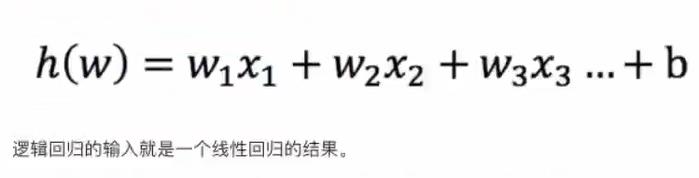
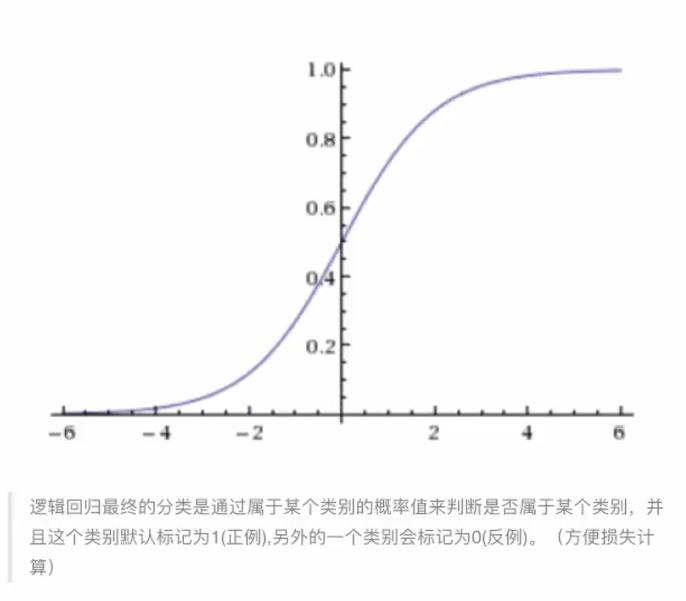
2、激活函数

sigmoid 函数：

g = 1/(1 + e^(-x))

下图公式是矩阵表示形式

注意： sigmoid 函数的输入就是公式中的 x，即：x = h(w)=w1x1+w2x2+w3x3…+b

3、损失以及优化

损失

逻辑回归的损失，称之为 对数似然损失

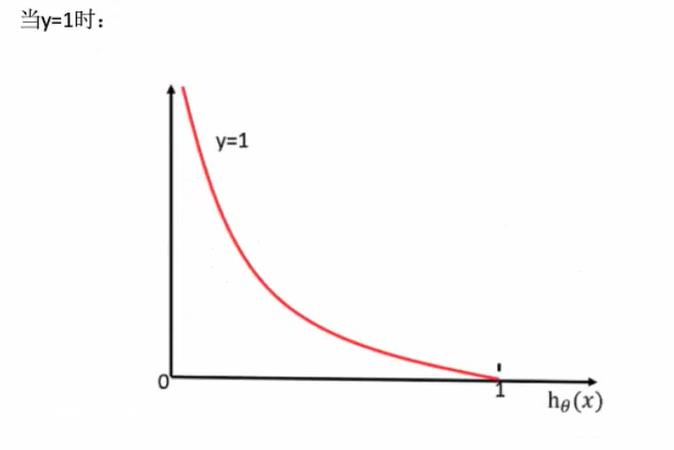
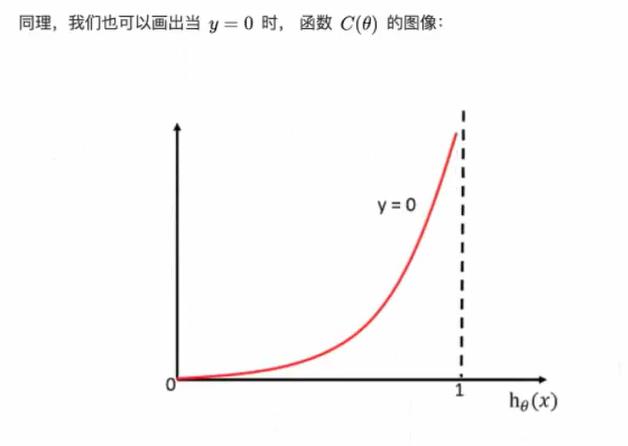
综合完整的损失函数

我们知道，-log§，P值越大，结果越小，所以我们可以对着这个损失的式子去分析。

优化损失

同样使用梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数， 提升原本属于1类别的概率，降低原本属于0类别的概率

4.4.3 逻辑回归的API

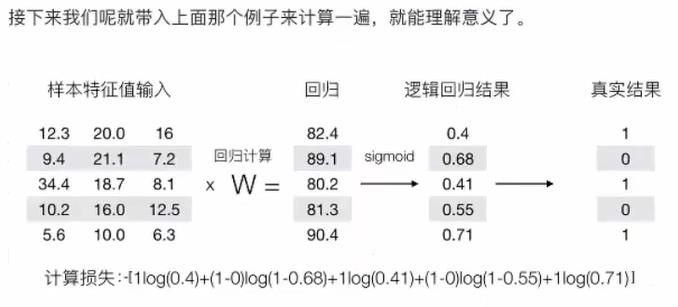
4.4.4 案例

癌症分类预测—良/ 恶性乳腺癌肿瘤预测

分析流程：

获取数据

读取的时候添加names

数据处理

处理缺失值

数据集划分

特征工程

无量纲化处理—标准化

逻辑回归预估器

模型评估

数据地址：archive.ics.uci.edu/ml/machine-…

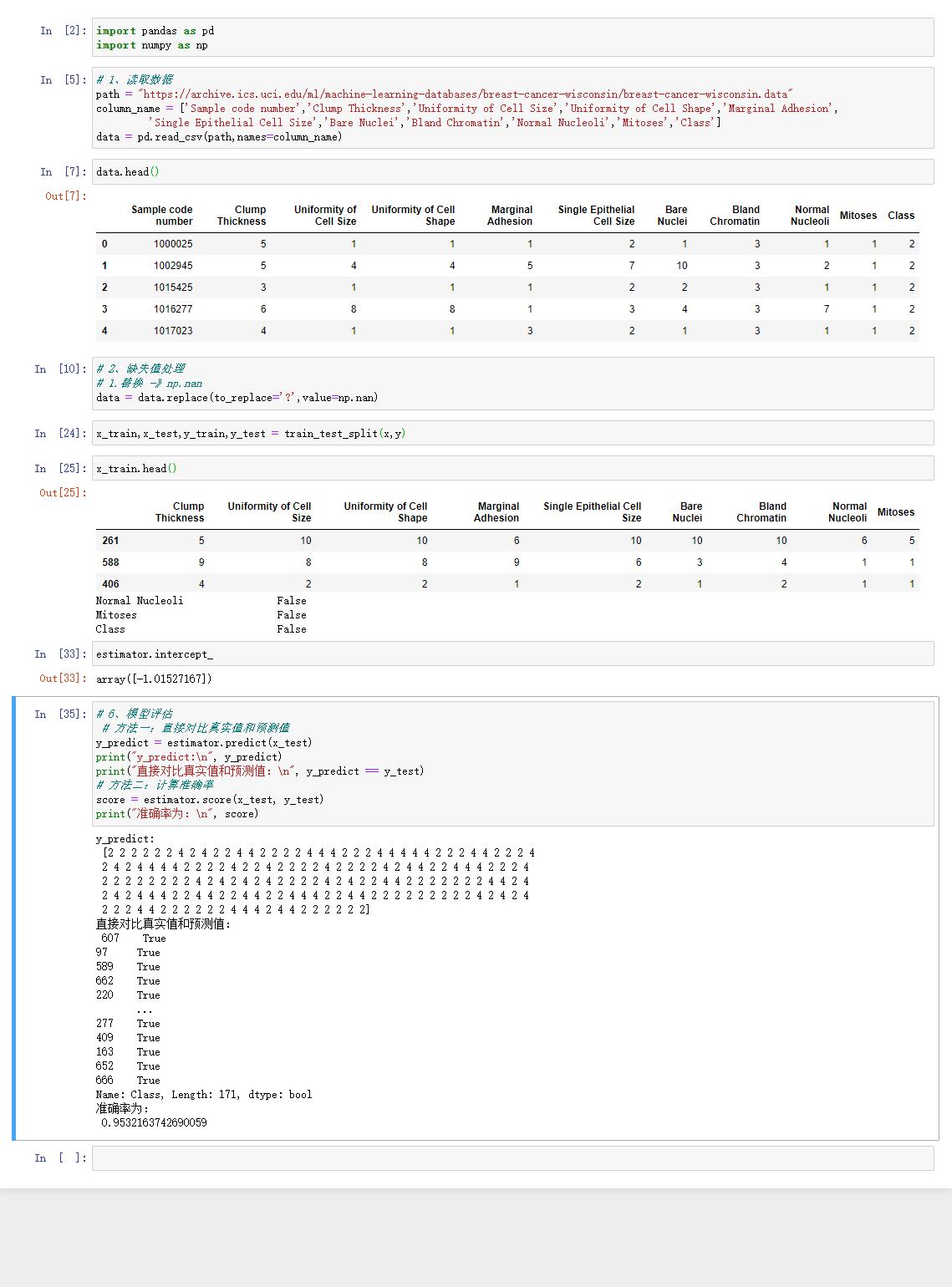
4.4.5 分类的评估方法

1、精确率和召回率

混淆矩阵

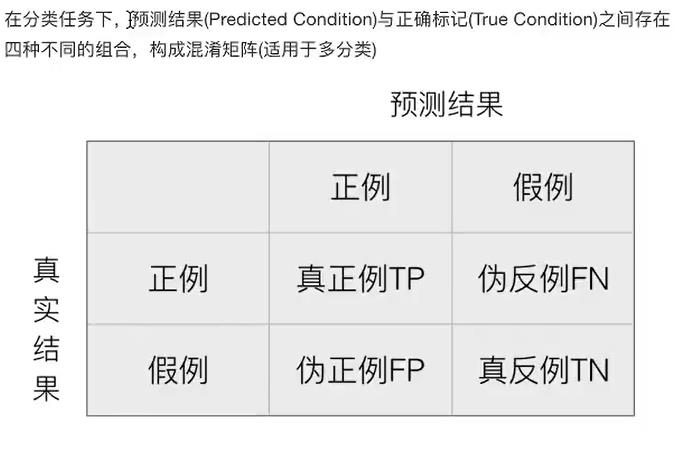
2、精确率（Precision）和召回率（Recall）

精确率：预测结果中正例样本中真实为正例的比例（了解）

召回率：真实为正例的样本中预测结果为正例的比例（查得全，对正样本的区分能力）

F1-score：反应了模型的稳健性

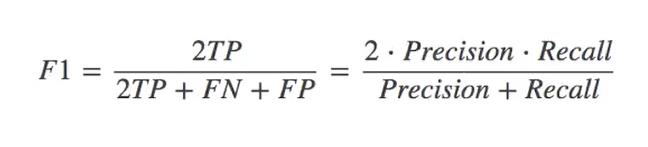
3、分类评估报告API

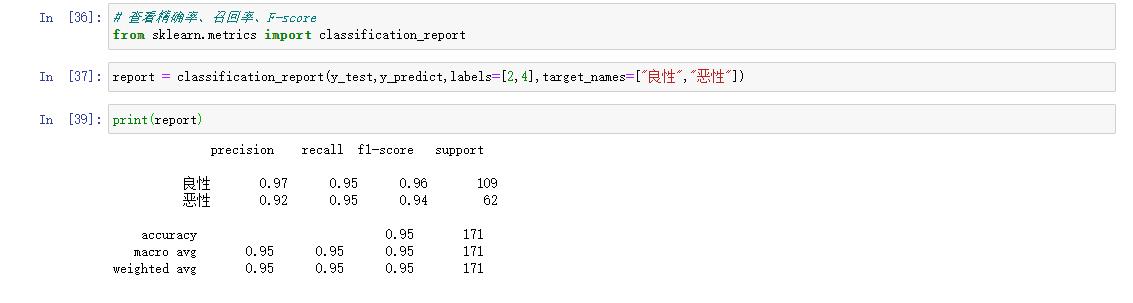
4、查看《癌症分类预测—良/ 恶性乳腺癌肿瘤预测》案例的精确率、召回率、F1-score

4.4.6 ROC曲线与AUC指标

1、TPR和FPR

（召回率）TPR = TP / (TP + FN)
所有真实类别为1的样本中，预测类别为1的比例

FPR = FP / (FP + TN)
所有真实类别为0的样本中，预测类别为1的比例

2、ROC曲线

ROC的横轴就是FPRate，纵轴就是TPRate，当二者相等时，表示意义是：对于不论真实类别是1还是0的样本，分类器预测值为1的概率是相等的，此时AUC指标为0.5

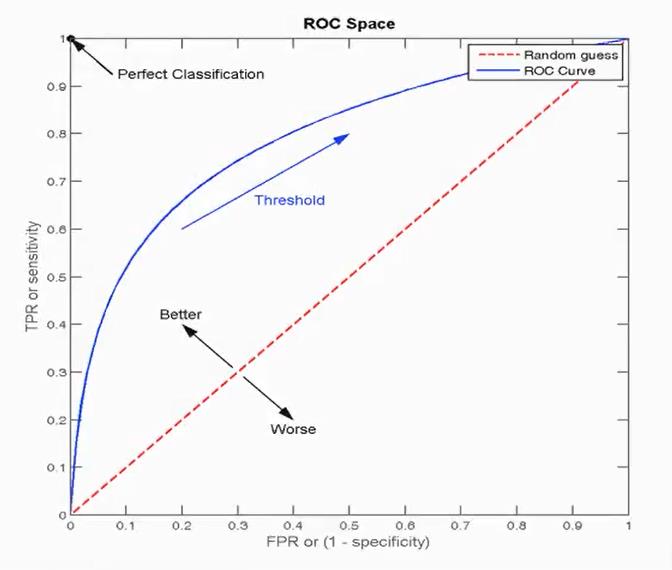
3、AUC指标

AUC的概率意义是随机取一对正负样本，正样本得分大于负样本的概率
AUC的最小值为0.5，最大值为1，取值越高越好
AUC=1，完美分类器，采用这
以上是关于Python机器学习笔记的主要内容，如果未能解决你的问题，请参考以下文章

机器学习40讲学习笔记13 线性降维

机器学习——预测数值型数据：回归

机器学习笔记：大话线性回归

机器学习数学|偏度与峰度及其python实现

机器学习---正则化

机器学习---正则化

Python机器学习笔记

Python机器学习笔记

一 机器学习概述

1.1 人工智能概述

1.1.1 机器学习与人工智能、深度学习关系

1.1.2 机器学习、深度学习能够做什么

1.2 什么是机器学习

1.2.1 定义

1.2.2 数据集构成

1.3 机器学习算法分类

1.3.1 监督学习

1.3.2 无监督学习

1.4 机器学习开发流程

1.5 学习框架和资料介绍

二 特征工程

2.1 数据集

2.1.1 可用数据集

2.1.2 sklearn数据集

2.1.3 数据集划分

2.2 特征工程介绍

2.2.1 为什么需要特征工程（Feature Engineering）

2.2.2 什么是特征工程

2.2.3 特征工程的位置与数据处理的比较

2.3 特征抽取

2.3.1 特征提取

2.3.2 字典特征提取

2.3.3 文本特征提取

2.4 特征预处理

2.4.1 概要

2.4.2 归一化

2.4.3 标准化

2.5 特征降维

2.5.1 降维

2.5.2 降维的两种方式

2.5.3 什么是特征选择

2.6 主成分分析

2.6.1 简介

2.6.2 案例

三 分类算法

3.1 sklearn转换器和估计器

3.1.1 转换器

3.1.2 估计器

3.2 K-近邻算法

3.3 模型选中与调优

3.3.1 交叉验证

3.4 朴素贝叶斯算法

3.4.1 什么是朴素贝叶斯分类方法

3.4.2 概率基础

3.4.3 联合概率、条件概率与相互独立

3.4.4 贝叶斯公式

3.4.5 API

3.4.6 案例

3.5 决策树

3.5.1 认识决策树

3.5.2 决策树原理

3.5.4 案例

3.5.6 决策树总结

3.6 集成学习方法之随机森林

3.6.1 什么 集成学习方法

3.6.2 什么是随即森林

3.6.3 随机森林原理过程

3.6.4 API

3.6.5 案例

四 回归与聚类算法

4.1 线性回归

4.1.1 线性回归的原理

4.1.2 线性回归的损失和优化原理

4.1.3 回归性能评估

4.1.4 正规方程和梯度下降对比

4.1.5 扩展

4.2 欠拟合和过拟合

4.2.1 简介

4.2.2 原因和解决方法

4.3 线性回归的改进—岭回归

4.3.1 带有L2正则化的线性回归—岭回归

4.4 分类算法—逻辑回归与二分类

4.4.1 逻辑回归

4.4.2 逻辑回归原理

4.4.3 逻辑回归的API

4.4.4 案例

一机器学习概述

二特征工程

三分类算法

3.6.1 什么集成学习方法

四回归与聚类算法