ZKP大爆炸

Posted 2022-09-12 mutourend

1. 引言

本文内容主要摘自ELI BEN-SASSON 2020年1月博客 A Cambrian Explosion of Crypto Proofs。

ZKP（Zero Knowledge Proof）为computational integrity（CI）证明系统的一个分支，近些年了，新的ZKP系统不断涌出，2019年出现的ZKP系统有：

• 1）Libra
• 2）Sonic
• 3）SuperSonic
• 4）PLONK
• 5）SLONK
• 6）Halo
• 7）Marlin
• 8）Fractal
• 9）Spartan
• 10）Succinct Aurora
• 11）REDSHIFT

以及相关实现：

• 1）https://github.com/0xProject/OpenZKP：Rust ZKP系统实现。
• 2）https://github.com/matter-labs/hodor：纯Rust zkSTARKs实现。
• 3）https://github.com/GuildOfWeavers/genSTARK：TypeScript zkSTARKs实现。
• 4）https://github.com/GuildOfWeavers/AirAssembly：验。为javascript runtime for AirAssembly——对computation Algebraic Intermediate Representation（AIR）进行编码的low-level语言，可将其编译为higher-level语言https://github.com/GuildOfWeavers/AirScript。

2. computational integrity（CI）证明系统

computational integrity（CI）证明系统主要解决影响去中心化区块链的2大问题：

• 1）隐私：ZKP在不牺牲integrity的前提下，通过保护计算中的某些输入，从而提供了隐私性。
• 2）扩容：Succinctly verifiable CI系统通过对验证大量交易integrity所需的计算量进行指数级的压缩，从而提供了扩容性。

所有的CI系统在代码实现时都有2个共同点：

• 1）Arithmetization算术化：为Prover对待证明的computational statement进行简化的过程。
• 2）Low-Degree compliance（LDC）低度兼容（或低度测试）：一种密码学手段，以确保Prover知道某些low-degree polynomials，且在Verifier选择的随机点上对这些low-degree polynomials进行evaluate。

2.1 Arithmetization 算术化

所谓算术化，是指将一些conceptual statement，如：
“I know the keys that allow me to spend a shielded Zcash transaction.”

转换为 包含了一组bounded-degree polynomials 的 algebraic statement，如：
“I know four polynomials $A(X),B(X),C(X),D(X)$, each of degree less than 1000, such that this equality holds: $A(X)\ast B^2(X)-C(X)=(X^{1000}-1)\ast D(X)$.”

2.2 Low-degree compliance LDC低度测试

所谓Low-degree compliance 低度测试：

• 是一种密码学手段，以确保Prover知道某些low-degree polynomials，且在Verifier选择的随机点上对这些low-degree polynomials进行evaluate。

仍然以2.1中的例子为例，一个好的LDC方案可确保：

• 当Verifier要求Prover回复各个多项式在随机$x_0$处的值时，确保Prover回复的$a_0=A(x_0),b_0=B(x_0),c_0=C(x_0),d_0=D(x_0)$。

但是，Prover可能会作弊，会在看到Verifier请求的$x_0$之后，再选择任意的多项式$A^{\prime }(X),B^{\prime }(X),C^{\prime }(X),D^{\prime }(X)$，取$a_0^{\prime }=A^{\prime }(x_0),b_0^{\prime }=B^{\prime }(x_0),c_0^{\prime }=C^{\prime }(x_0),d_0^{\prime }=D^{\prime }(x_0)$，使得KaTeX parse error: Double superscript at position 10: a'_0*b'_0^̲2-c'_0=(x_0^10…验证通过，从而可成功欺骗Verifier。而$a_0^{\prime },b_0^{\prime },c_0^{\prime },d_0^{\prime }$并不是之前所选择的low-degree polynomials $A(X),B(X),C(X),D(X)$在$x_0$处的evaluation值。
因此，需要采用一种密码学手段来避免类似的攻击。（一种直观的解决方案是，Prover将整个$A(X),B(X),C(X),D(X)$多项式直接发送给Verifier，但这样既不满足扩容性，也不满足隐私性。）

考虑到这些，CI证明系统可根据如下内容进行分类：

• 1）用于强化LDC低度测试所用的密码学原语；
• 2）基于这些元素所构建的特定的LDC解决方案；
• 3）该选择所支持的算术化类型。

2. CI证明系统对比分类

2.1 根据密码学假设分类

从高层来看，不同的CI系统的最大理论区分度在于其安全性是否需要 对称原语 还是 非对称原语：

常见的对称原语有：

• SHA2
• Keccak（SHA3）
• Blake

通常认为这些对称原语是抗碰撞的哈希函数，具有伪随机性，且可作为random oracle。

常见的非对称原语有：

• DLP（Discrete Logarithm Problem）：解决DLP modulo a prime number, an RSA modulus, or in an elliptic curve group的难度。
• unknown order group：计算某RSA ring的乘法群的size的难度。
• knowledge of exponent assumption
• adaptive root assumption

根据CI证明系统的安全假设是基于对称还是非对称密码学原语，可进一步分类为：

• 1）计算效率【对称CI系统可基于任意field进行算术化，可实现更高的效率。】
  当前代码中所实现的基于非对称原语的安全性，要求需基于large algebraic domain来进行算术化并解决LDC问题。所谓large algebraic domain是指：

  • 1.1）large prime fields和large elliptic curves，使得每个field/group element具有数百bits长
  • 1.2）或 integer rings，每个元素为数千bits长。

  而若基于对称原语构建，可基于任意algebraic domain（ring或finite field均可以）进行算术化并解决LDC问题。仅要求相应的algebraic domain（ring或finite field均可以）包含smooth sub-groups（包括very small binary fields and 2-smooth smooth prime fields（64bits或更少），使得arithmetization运算可快速完成）。【所谓field is k-smooth if it contains a subgroup (multiplicative or additive) of size all of whose prime divisors are at most k. For instance, all binary fields are 2-smooth, and so fields of size q such the q-1 is divisible by a large power of 2.】
  对称CI系统可基于任意field进行算术化，可实现更高的效率。

• 2）抗量子安全性【仅对称原语是plausibly post-quantum secure的。】
  当前所有的使用非对称原语的CI系统都可被（未来可出现的）具有足够大qubits的量子计算机破解。
  而对称原语，是plausibly post-quantum secure的。

• 3）Future-Proofing【对于金融基础设施来说，使用新的非对称假设的风险更大】
  林迪效应理论认为“一些不易腐烂的东西，如技术或想法的未来寿命与其当前年龄成正比。”或者简单地说，旧东西比新东西存活的时间更长。在密码学领域，这可以解释为，依赖于较旧的、经过战斗测试的原语的系统比轮胎磨损较少的新假设更安全，更能future-proof。
  
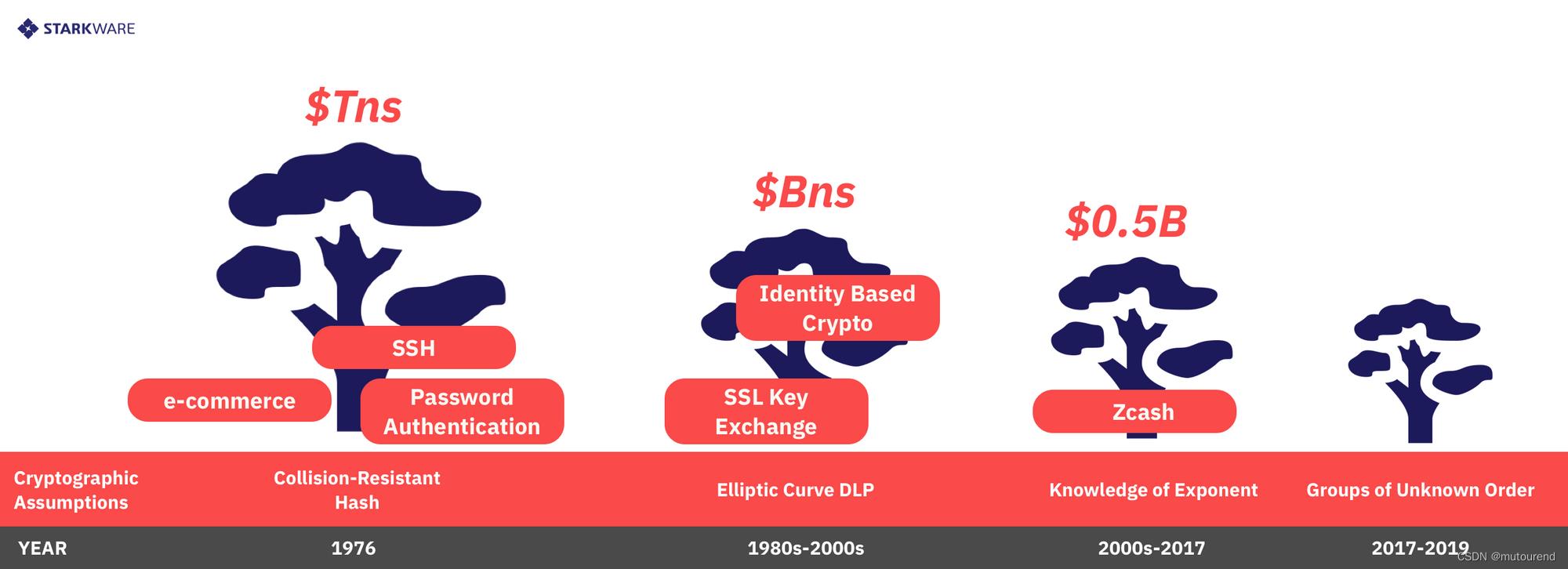
  从这个角度来说，新的非对称密码学假设（如groups of unknow order、generic group model以及knowledge of exponent assumption）都更年轻，与旧的假设相比（如用于数字签名、基于身份的加密和SSH初始化的更标准的DLP和RSA假设），所支持的经济体量更轻。与现有的抗碰撞哈希对称假设相比，这些新的假设具有less future-proof，因为后一种假设（甚至是特定的哈希函数）已作为基石广泛用于保护计算机、网络、互联网和电子商务的实体之中。
  此外，这些假设之间有严格的数学层次。CRH假设在该层次结构中占主导地位，因为如果该假设被破解（意味着无法找到安全的密码学哈希函数），则特别地，RSA和DLP假设也会被破解，因为这些假设意味着存在良好的CRH！类似地，DLP假设优于knowledge of exponent（KoE）假设，因为如果前者（DLP）假设不成立，则后者（KoE）也将不成立。同样，RSA假设优于group of unknown order（GoUD）假设，因为如果RSA被破解，则GoUD也会被破解。

• 4）Argument Length（证明长度）【asymmetric circuit-specific systems (Groth16) are shortest, shorter than all asymmetric universal ones, and all symmetric systems。】
  以上三个方面的对比都认为对称CI要优于非对称CI。但是若从证明长度来考虑，则非对称CI的优势更明显。
  非对称CI的communication complexity（或证明长度）要比对称CI小一到三个量级。
  著名的Groth16 SNARK在128-bit安全等级情况下，其proof size小于200 bytes。而相同安全等级情况下，当今所有对称CI的proof size为几十kB。当然，并不是所有的对称CI proof size都as succinct as 200 bytes。
  当前基于Groth16的优化有：

  • 4.1）移除了可信设置，使其是透明的
  • 4.2）处理通用电路（Groth16需对每个电路都做一次可信设置）

  优化后的Groth16的proof size要更大写，约为500 bytes左右（如PLONK）到 十几kB（与对称CI接近）。

因此，小结下：

• 1）对称CI系统可基于任意field进行算术化，效率更高；
• 2）仅对称CI系统具有plausibly post-quantum secure；
• 3）在金融基础设施中使用新的非对称假设风险更大；
• 4）asymmetric circuit-specific systems (Groth16) are shortest, shorter than all asymmetric universal ones, and all symmetric systems。

2.2 按LDC低度测试方案分类

有2种方式来实现LDC：

• 1）hiding queries
• 2）commitment scheme

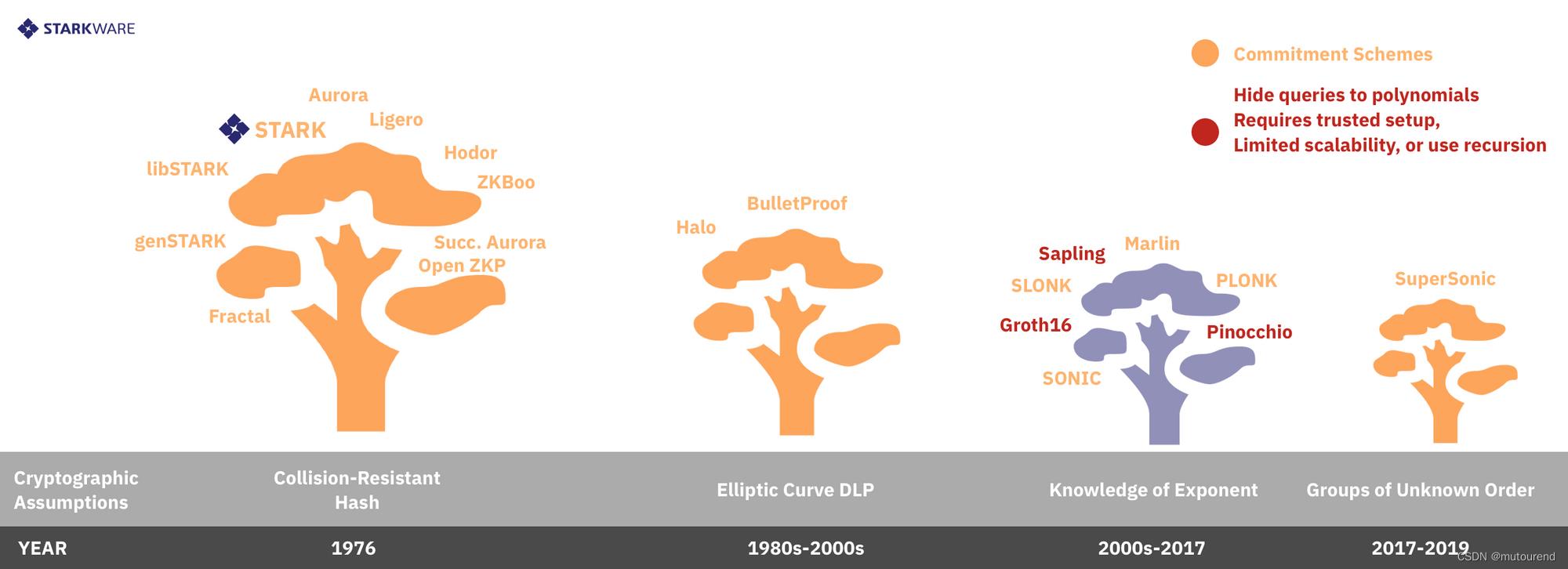
2.2.1 Hiding Queries LDC低度测试方案

Hiding Queries形成于2013年Succinct Non-Interactive Arguments via Linear Interactive Proofs论文中。
Zcash-style SNARKs（如Pinocchio、libSNARK、Groth16）采用的是Hiding Queries LDC低度测试方案。
为了获得Prover的回复，采用同态加密来隐藏（或加密）$x_0$，并提供足够的信息使得Prover可evaluate $A,B,C,D$ on $x_0$。事实上，给Prover提供的信息为a sequence of encryptions of powers of $x_0$（即，encryptions of $x_0^1,x_0^2,\cdots ,x_0^{1000}$），使得Prover可evaluate any degree-1000 polynomial，但是这些多项式的degree最大不会超过$1000$。粗略来说，该系统是安全的，因为Prover不知道$x_0$的具体值，且该$x_0$是提前随机选定的，因此，若Prover想作弊大概率将暴露。
需要一种可信的预处理设置阶段来sample $x_0$并encrypt the sequence of powers above（以及其它额外信息），从而使得Proving Key至少与待证明电路的多项式degree是一样大的，同时，有一个相对小很多的Verification Key。一旦设置完成并发布了相应的PK/VK，则每个proof都是SNARK（succinct noninteractive argument of knowledge）证明。注意，这样的系统在预处理阶段需要某些形式的交互，这在理论上是无法避免的。同时该系统也不是透明的，即意味着用于生成和加密$x_0$的熵不能是公开随机值，因为一旦任何人知道$x_0$，都可破解该系统并伪造证明。在不泄露 x 0 x_0 x宇宙大爆炸！宇宙的时间序列表！

STARK Low Degree Testing——FRI

企业大数据平台的数据仓库架构

ZKP应用：石头剪刀布游戏

大数据企业大数据平台的数据仓库架构大数据和人工智能的关系

掌握6大模块7个核心概念！帮你搞定Mycat中间件#导入MD文档图片#