STARK Low Degree Testing——FRI
Posted mutourend
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了STARK Low Degree Testing——FRI相关的知识,希望对你有一定的参考价值。
1. 引言
前序博客有:
- ZKP大爆炸
- STARKs and STARK VM: Proofs of Computational Integrity
- STARK入门知识
- STARK中的FRI代码解析
- Rescue-Prime hash STARK 代码解析
- Fast Reed-Solomon Interactive Oracle Proofs of Proximity学习笔记
Low Degree Testing低度测试为STARK证明succinctness的秘方。
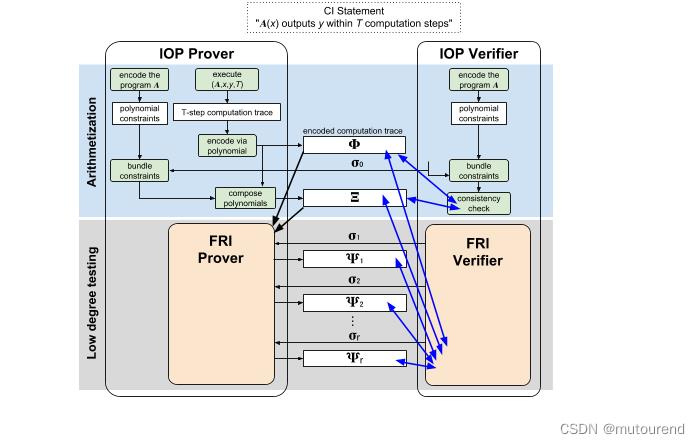
在STARK中,通过Arithmetization将Computational Integrity问题reduce为low degree testing问题。
所谓low degree testing低度测试,是指,若要判定某函数是否为具有某指定上限degree的多项式,仅需要make a small number of queries to the function。
低度测试问题已研究了二十多年,是probabilistic proof理论的核心工具。本文重点在于详细解释低度测试,并介绍FRI协议——STARK中所用的低度测试解决方案。
2. 低度测试
低度测试针对的场景为:
给定某函数,仅查询该函数的 “少量” 位置,来判定该函数是否为 小于某常量
d
d
d degree的某多项式。
即,已知某域
F
F
F的子集
L
L
L和degree bound
d
d
d,判定
f
:
L
→
F
f:L\\rightarrow F
f:L→F是否等于某degree小于
d
d
d的多项式,即,是否存在多项式:
p
(
x
)
=
c
0
+
c
1
x
+
⋯
+
c
d
−
1
x
d
−
1
p(x)=c_0+c_1x+\\cdots+c_d-1x^d-1
p(x)=c0+c1x+⋯+cd−1xd−1
over
F
F
F,其中对于
∀
a
∈
L
\\forall a\\in L
∀a∈L,有
p
(
a
)
=
f
(
a
)
p(a)=f(a)
p(a)=f(a)。
可想象field size很大,如为
2
128
2^128
2128,
L
L
L的size约为1千万(10,000,000)。
为解决该问题,需要query f f f at 整个 L L L域,因 f f f可能仅在 L L L中的某个单点不满足 p ( a ) = f ( a ) p(a)=f(a) p(a)=f(a)。即使我们允许一定概率的错误,所需query的次数仍然与 L L L的size呈线性关系。
低度测试,通过构建probabilistic proof,将query number降为logarithmic in ∣ L ∣ |L| ∣L∣(如 L ≈ 10 , 000 , 000 ,则 log 2 ( L ) ≈ 23 L\\approx10,000,000,则\\log_2(L)\\approx 23 L≈10,000,000,则log2(L)≈23),可解决上述问题。确切来说,分为如下2种情况:
- 1)第一种情况——若函数 f f f等于某低度多项式:即存在多项式 p ( x ) p(x) p(x) over F F F,其degree小于 d d d,并agrees with f f f everywhere on L L L。
- 2)第二种情况——若函数 f f f为far from ALL low degree polynomials:如,需调整 f f f中至少 10 % 10\\% 10%的值,才能获得一个与degree小于 d d d多项式一致的函数 f ′ f' f′。
还有一种可能性是:
- 3)第三种情况——若函数 f f f中度接近某低度多项式,但不等于任何低度多项式。如,某函数具有 5 % 5\\% 5%的值不等于低度多项式,因此不符合以上两种情况。但是,之前的STARK arithmetization步骤中,确保了本情况不会发生。即,诚实的Prover在处理true statement算术化过程中,会落入第一种情况;而作弊的Prover在试图证明false claim时,将大概率落入第二种情况。
为了区分以上两种情况,将使用a probabilistic polynomial-time test来query f f f at a small number of locations。
【
- 若 f f f确实是低度的,则该测试通过的概率为 1 1 1。
- 若 f f f为far from low degree,则该测试将大概率不通过。
- 若
f
f
f为
δ
\\delta
δ-far from any function degree less than
d
d
d(即,必须修改至少
δ
∣
L
∣
\\delta|L|
δ∣L∣ 个位置来获得某个degree小于
d
d
d的多项式),则测试被拒绝的概率不低于
Ω
(
δ
)
\\Omega(\\delta)
Ω(δ)(或其它“nice” function of
δ
\\delta
δ)。直观来说,若
δ
\\delta
δ越接近零,则区分这两种情况的难度越大。
】
接下来将一种简单的低度测试方案,并解释其为何无法满足要求,然后介绍一种效率指数级提升的复杂低度测试方案——STARK中使用的FRI。
2.1 Direct Test 低度测试方案
Direct Test 低度测试方案是:
通过采用
d
+
1
d+1
d+1次query,来判断某函数是否为(或接近为)某degree小于
d
d
d的多项式。
Direct Test 低度测试方案 基于的多项式basic fact为:
- 任意degree小于 d d d的多项式,可由 F F F中任意 d d d个不同位置的值唯一确定。
该fact源自:degree为 k k k的多项式,最多具有 k k k个roots in F F F。
Direct Test 低度测试方案中,query次数为 d + 1 d+1 d+1,远小于 f f f的domain size ∣ L ∣ |L| ∣L∣。
首先讨论2个简单的特例情况:
-
1)若函数 f f f为constant function,即 d = 1 d=1 d=1:则低度测试问题转为区分 f f f为某constant function( f ( x ) = c f(x)=c f(x)=c for some c c c in F F F) 还是 f f f为far from any constant function。
针对这种特例情况,仅需要2-query test即可:query f f f at 某固定点 z 1 z_1 z1以及某随机点 w w w,然后检查 f ( z 1 ) = f ( w ) f(z_1)=f(w) f(z1)=f(w)是否成立即可。直观的, f ( z 1 ) f(z_1) f(z1)可决定 f f f的常量值, f ( w ) f(w) f(w)测试是否所有的 f f f都接近该常量值。 -
2)若函数 f f f为线性函数,即 d = 2 d=2 d=2:则低度测试问题转为区分 f f f为某线性函数( f ( x ) = a x + b f(x)=ax+b f(x)=ax+b for some a , b a,b a,b in F F F) 还是 f f f为far from any linear function。
针对这种特例情况,仅需要3-query test即可:query f f f at 某2个固定点 z 1 , z 2 z_1,z_2 z1,z2以及某随机点 w w w,然后检查 ( z 1 , f ( z 1 ) ) , ( z 2 , f ( z 2 ) ) , ( w , f ( w ) ) (z_1,f(z_1)),(z_2,f(z_2)),(w,f(w)) (z1,f(z1)),(z2,f(z2)),(w,f(w))是否共线性。直观的, f ( z 1 ) 和 f ( z 2 ) f(z_1)和f(z_2) f(z1)和f(z2)可决定 f f f线性函数, f ( w ) f(w) f(w)测试所有 f f f值是否都在该线上。
将以上特例情况推广至具有degree bound
d
d
d的通用情况:
query
f
f
f at
d
d
d个固定点
z
1
,
z
2
,
⋯
,
z
d
z_1,z_2,\\cdots,z_d
z1,以上是关于STARK Low Degree Testing——FRI的主要内容,如果未能解决你的问题,请参考以下文章