配送路径规划基于matlab遗传算法求解带时间窗的含充电站配送车辆路径规划问题含Matlab源码 509期

Posted 2022-05-27 海神之光

一、城市配送系统简介

城市配送系统(city delivery system,CDS)的发展是一个城市提高其公共运输能力的关键。目前国内外许多学者对CDS系统进行了深入研究。其中,车辆路径优化问题是城市配送系统中的重要环节,通过对车辆行驶路径的优化管理可以有效地降低城市配送成本,同时可以提高城市交通效率,节省公共资源,无论对企业还是对社会,都具有重要的意义。本文针CDS的车辆路径规划问题,采用遗传算法(genetic algorithm,GA)作为优化方法,提出一种配送车辆路径规划的设计方案,以实现车辆路径选取的最优决策。

1 配送车辆路径规划
1.1 城市配送系统
城市配送系统的功能构架如图1所示。城市配送系统是联系供应商、信息中心、仓库和消费者之间的重要纽带。

城市配送系统的主要构成如图2所示,其中城市配送网络子系统负责监管城市交通信息,城市配送运营调度系统负责对配送车辆进行调度,城市配送监管系统负责对配送车辆的任务执行情况进行监督管理和实时纠错,城市配送信息处理系统负责对相关信息进行实时分析和处理。GDS系统中较为关键的问题是在上述职能范围内,如何构建一个最优运行框架来实现最优化的配送效益。

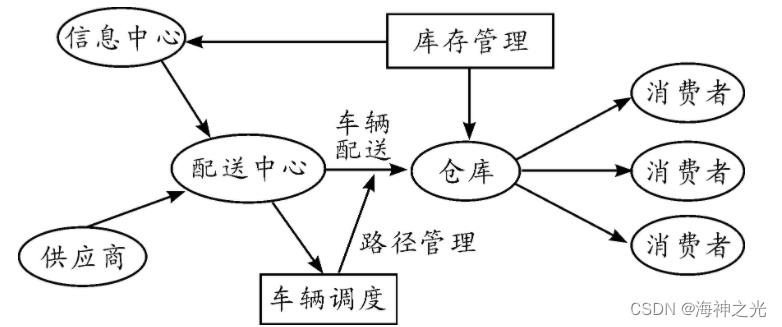
图1 配送系统功能构架

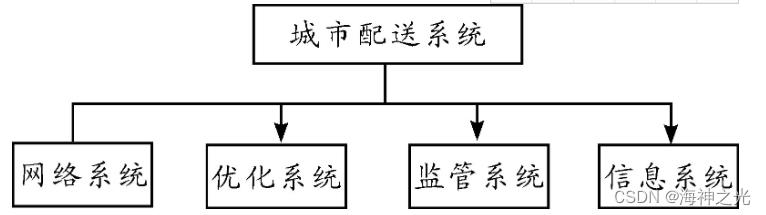
图2 城市配送系统的组成

1.2 车辆路径优化的意义
车辆路径规划(vehicle routing problem,VRP)自从1959年被Dantzig和Ramse提出的之后,迅速引起各领域工程师和管理学者的极大重视,成为工程管理领域的重点和热点问题。

VRP问题是城市配送系统的主要优化问题之一,在城市配送系统中具有重要的意义。从企业运作和社会环保、节能的角度而言,VRP研究的研究意义具体可以概括为以下方面:

1. 通过对配送路线的合理优化,可以有效提高配送效率,从而缩短配送时间,提高服务质量和客户满意度;
2. 通过对配送路线的合理优化,可以有效地降低运输成本,节省资金;
3. 有通过对配送路线的合理优化,可以有效降低车辆占用公路的时间,从而可以缓解交通,减少噪声、尾气排放等运输污染。

2 VRP问题的数学描述
为了便于研究VRP问题的优化策略,首先对VRP问题进行数学描述。假设配送中心和仓库的地理位置均为固定且已知,则仓库与配送中心以及仓库间的位置信息可以由路径距离矩阵描述为

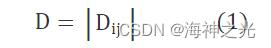
VRP可行解可以描述为一系列行驶路径的决策的集合,即

其中,ki表示第i条路段决策结果。
VRP优化目标由成本最小化来描述,即运输过程中所产生的固定成本和运输费用,如式(3)所示。

其中:TV为配送车辆在运输过程中的总成本;Ns为运输途中的固定费用;ξ(ki)为在第ki路段上的花费,正比于ki路段的行驶里程,计算式为

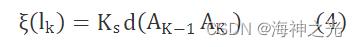
其中: d(·)为距离运算符;Ks为单位里程所需的费用;AK为仓库节点标号。
考虑到在实际配送过程中有许多的条件限制,因此在目标函数上施加一定的约束条件,主要包括:车辆配送过程中所携带的货物量存在上限,且车辆完成配送任务之后须返回出发点以备下次配送任务。

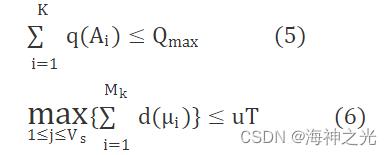
其中 :Qmax为配送车辆承重上限;q(·) 为载运重量计算符;u为平均车速;T 为配送任务所要求的最大时间限度。

3 VRP问题的遗传算法优化
结合上述模型,基于遗传算法来解决所提出的VRP问题,基本参数设定为:种群M为20,最大代数G为100,交叉概率Pc为0.8,变异概率Pm为 0.1,首先对VRP问题的可行解进行编码并生产初始种群,整个算法实施步骤如图3所示。根据目标函数设计适配度,终止条件设计为:

1. 当最优解连续5代不发生变化;
2. 当迭代步数超过300步。
   对于初始种群根据数学模型的输入条件,进行适配度计算并根据适配度计算结果进行种群选择操作。

3.1 编码规则
根据VRP问题的特点,本文采用浮点数编码方案,首先将各个仓库的节点数转换为相对应的随机浮点数,同时将送货中心(即配送过程的起点)作为第一个浮点数,考虑到编程的方便,将送货中心同时作为终点放入到最后一个浮点数,计算式为

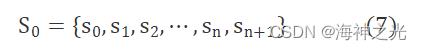
其中:s0为生产中心所对应的浮点数;s1~sn为n个仓库所对应的浮点数。
越小的浮点数对应有越高的优先级,例如对于染色体
S: 0.01 0.35 0.38 0.65 0.81 0.25 0.99
A0 A1 A2 A3 A4 A5 A0
其对应的表现型为
K:A0→A5→A2→A3→A4→A5→A0
起点s0至为0.01,终点sn+1置为0.99,起点与终点参与编程,但不参与到选择、交叉与变异。

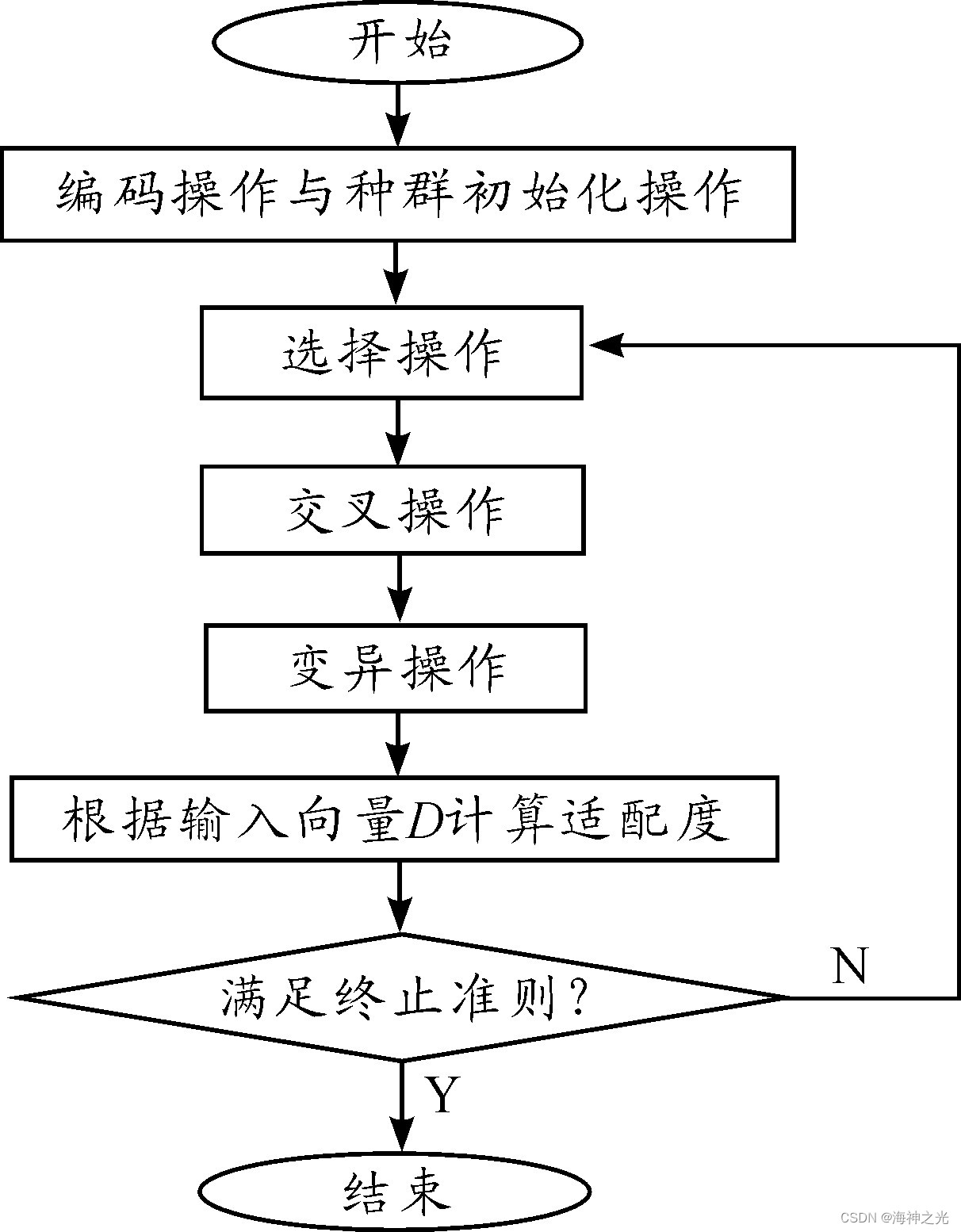
图3 基于遗传算法的算法流程

3.2 适配度函数
根据上述编码规则,对每一个可行解都可以计算出整个配送过程中的行驶路线,将行驶总距离作为适配度函数

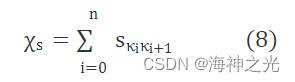
其中χs表示第s个可行解的适配度。

3.3 遗传算子设计
在上述基础上对遗传算法进行选择算子、交叉算子和变异算子的设计。

1. 选择算子
   对种群中的20个可行解根据适配度值来选择排序靠前的10个染色体作为选择结果,放入后代中继续后续操作。
2. 交叉算子
   对于选定的两个父代个体,随机选择一个交叉位置,将其中一个父代中的前t个基因作为子代个体的前t个基因,同时将第2个父辈染色体X2的后n-t个基因取出作为子代的后n-t个基因,如图4所示。
   
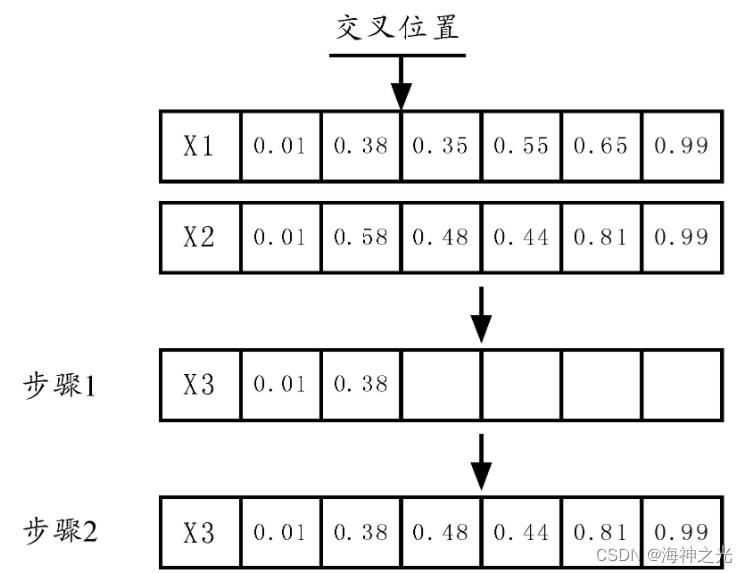
   图4 交叉操作示意图
3. 变异算子
   首选按照变异概率来决定发生变异的位,然后变异操作采用取逆算子
   

二、部分源代码

clc
clear
close all
tic
data = xlsread('数据2.xlsx',1,'A:F');
position = data(:,2:3);
demand = data(:,4);
ET = data(:,5);         % 早到时间
LT = data(:,6);         % 晚到时间

CarLoad = 200;            % 汽车最大载重量
CarDist = 300;          % 汽车续航里程
CarDistance = 3000;     % 汽车最大行驶距离
CityNum = 23;           % 需求点数量
CarNum = 3;
ChargeNum = 2;      % 充电桩数量
NP = 200;           % 种群大小
maxgen = 500;       % 最大进化代数
Pc = 0.8;           % 交叉概率
Pm = 0.2;           % 变异概率
Gap = 0.9;          % 代沟(Generation gap)
speed = 50;
fitmax = 10000000;
% c0 = 200;
c1 = 3;
c2 = 50;             % 充电一次的费用

% ST = [0; ones(CityNum + ChargeNum,1) * 0.0005];   % 服务时间

ST =  0.0005;   % 服务时间


CE = 10;   % 早到惩罚系数
CL = 24;   % 晚到惩罚系数
%% 计算各城市之间的距离
distance = zeros(CityNum+1 + ChargeNum);
for i =  1 : CityNum + ChargeNum + 1
    for j = i + 1 : CityNum + ChargeNum + 1
        distance(i,j) = ((position(i,1)-position(j,1))^2+(position(i,2)-position(j,2))^2)^0.5;
        distance(j,i) = distance(i,j);
    end
end

三、运行结果

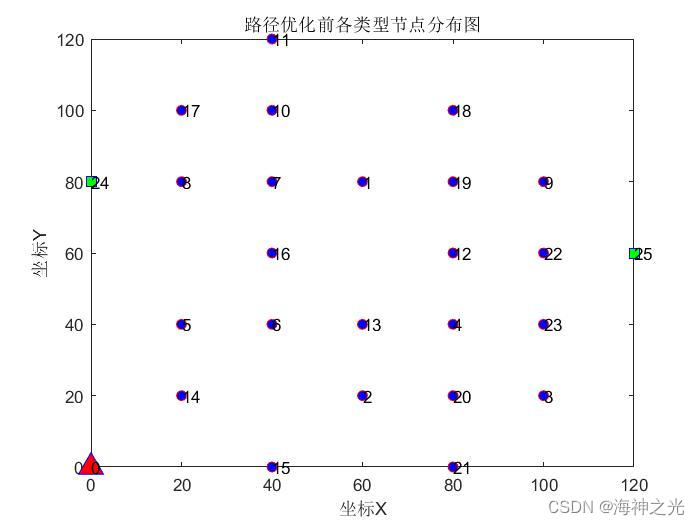
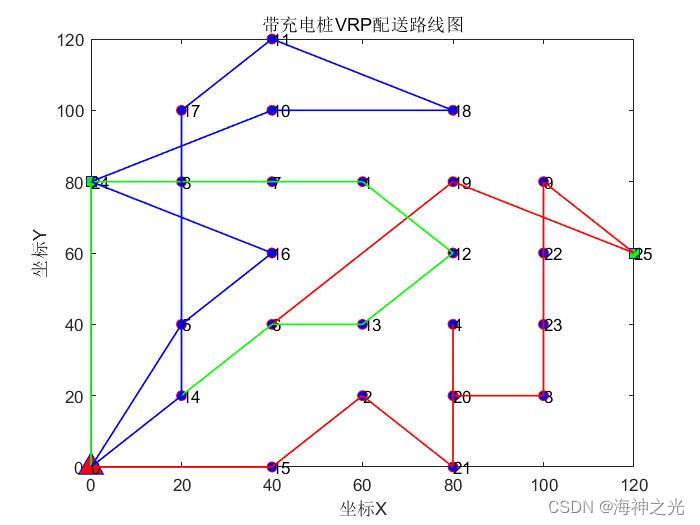
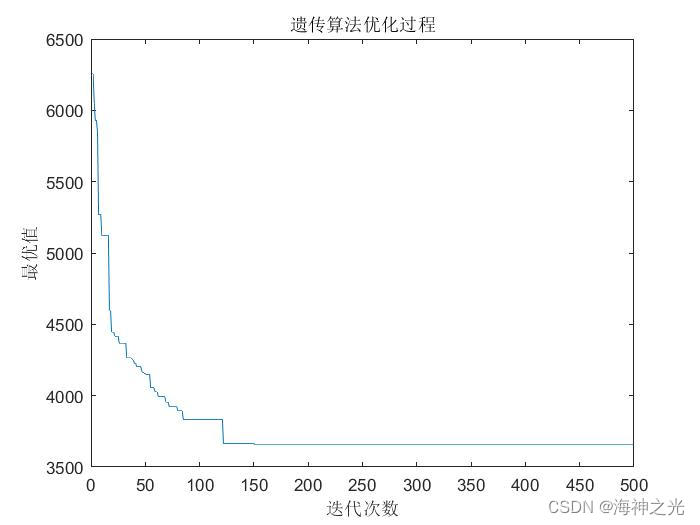
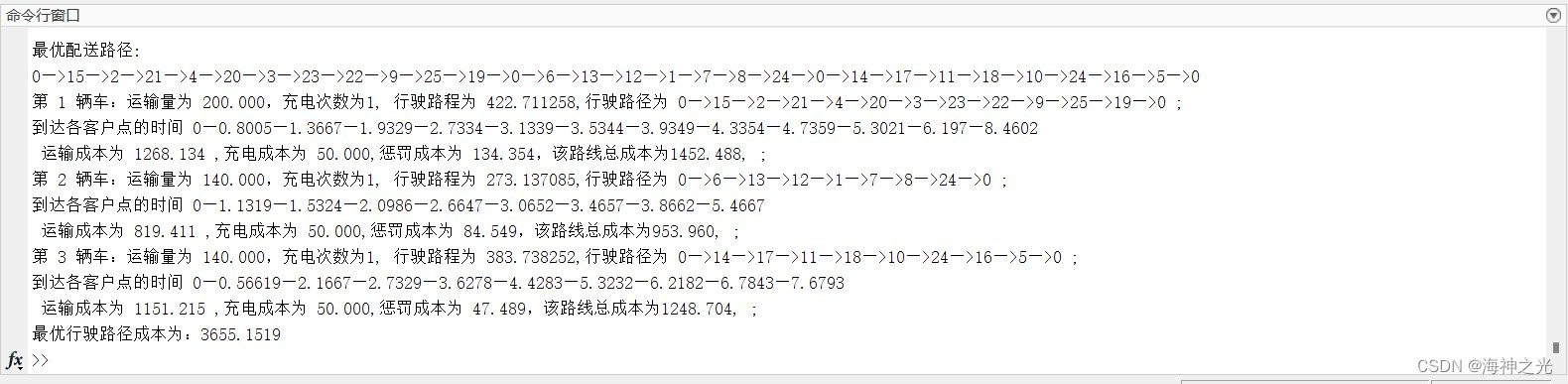
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]郭秀红.基于遗传算法的配送车辆路径规划[J].四川兵工学报. 2013,34(01)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除