详解Java算法之冒泡排序(Bubble Sorting)
Posted 虫链Java Library
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了详解Java算法之冒泡排序(Bubble Sorting)相关的知识,希望对你有一定的参考价值。
冒泡排序基本介绍
冒泡排序(Bubble Sorting)的基本思想是通过对待排序序列从前向后(从下表较小的元素开始),以此比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前向后部,就像水底下的气泡一样逐渐向上冒。

文章目录
冒泡排序应用实例
我们举一个具体的案例来说明冒泡排序法,我们将几个无序的数:3,6,4,2,11,10,5 使用冒泡排序法将其排成一个从小到大的有序数列。

看上面的图解可能有些小伙伴不好理解,不过没关系下面我们更详细的给大家列出排序细节。
原始数组为:3,6,4,2,11,10,5 下面进行第一趟排序
- 3与6进行比较,3 < 6 所以不交换位置。得到
3,6,4,2,11,10,5 - 6与4比较,6 > 4,6与4交换位置,如果相邻的元素逆序就交换。得到
3,4,6,2,11,10,5 - 交换完位置后两个索引又同时移动让 6 与 2比较,6 > 2,6与2交换位置。得到
3,4,2,6,11,10,5 - 6与11进行比较,6 < 11 所以不交换位置。得到
3,4,2,6,11,10,5 - 11与10进行比较,11 > 10 所以进行位置交换。得到
3,4,2,6,10,11,5 - 最后将11与5进行比较,11 > 5 所以进行位置交换。得到
3,4,2,6,10,5,11
第一趟排序的最终结果为:3,4,2,6,10,5,11 下面进行第二趟排序
- 3与4进行比较 3 < 4 所以不进行交换。得到
3,4,2,6,10,5,11 - 4与2进行比较 4 > 2 所以进行位置交换。得到
3,2,4,6,10,5,11 - 4与6进行比较 4 < 6 所以不进行位置交换。得到
3,2,4,6,10,5,11 - 6与10进行比较 6 < 10 所以不进行位置交换。得到
3,2,4,6,10,5,11 - 10与5进行比较 10 > 5 所以进行位置交换。得到
3,2,4,6,5,10,11
需要注意的是每趟运行过后最后一个数就会被确认下来,不在进行比较交换。现在我们重新回到上方排序交换图,是不是思路一下就清晰起来了?
冒泡排序规则总结:
- 一共进行数组大小 -1次循环
- 每一趟排序的次数在逐渐的减小
- 如果我们发现在某趟排序中,没有发生一次交换可以提前结束排序,这个就是优化。
代码实现
原始数组为:3,6,4,2,11,10,5 下面进行第一趟排序
public static void main(String[] args)
int arr[] = 3, 6, 4, 2, 11, 10, 5;
//为了容易理解,我们把冒泡排序的演变过程,给大家展示一下。
//第一趟排序,就是将最大的数排在最后
int temp = 0; //临时变量
for (int j = 0; j < arr.length - 1; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第一趟排序后的数组");
System.out.println(Arrays.toString(arr));
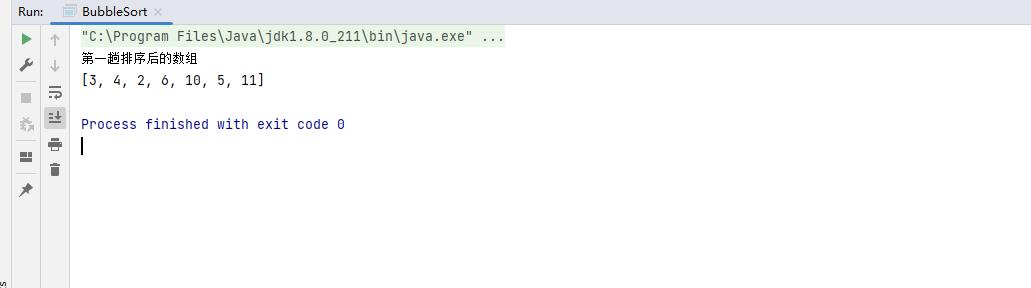
第一趟排序的最终结果为:3,4,2,6,10,5,11 下面进行第二趟排序
public static void main(String[] args)
int arr[] = 3, 6, 4, 2, 11, 10, 5;
//为了容易理解,我们把冒泡排序的演变过程,给大家展示一下。
//第一趟排序,就是将最大的数排在最后
int temp = 0; //临时变量
for (int j = 0; j < arr.length - 1; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第一趟排序后的数组");
System.out.println(Arrays.toString(arr));
//第二趟排序,就是将第二大的数排在倒数第二位
for (int j = 0; j < arr.length - 1 - 1; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第二趟排序后的数组");
System.out.println(Arrays.toString(arr));
第二次排序后得到得最终结果为:3, 2, 4, 6, 5, 10, 11 以此类推下面我们直接进行六次排序看看最终的结果是否与我们预期的一致。
public static void main(String[] args)
int arr[] = 3, 6, 4, 2, 11, 10, 5;
//为了容易理解,我们把冒泡排序的演变过程,给大家展示一下。
//第一趟排序,就是将最大的数排在最后
int temp = 0; //临时变量
for (int j = 0; j < arr.length - 1; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第一趟排序后的数组");
System.out.println(Arrays.toString(arr));
//第二趟排序,就是将第二大的数排在倒数第二位
for (int j = 0; j < arr.length - 1 - 1; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第二趟排序后的数组");
System.out.println(Arrays.toString(arr));
//第二趟排序,就是将第三大的数排在倒数第三位
for (int j = 0; j < arr.length - 1 - 2; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第三趟排序后的数组");
System.out.println(Arrays.toString(arr));
//第二趟排序,就是将第四大的数排在倒数第四位
for (int j = 0; j < arr.length - 1 - 3; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第四趟排序后的数组");
System.out.println(Arrays.toString(arr));
//第二趟排序,就是将第五大的数排在倒数第五位
for (int j = 0; j < arr.length - 1 - 4; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("第五趟排序后的数组");
System.out.println(Arrays.toString(arr));
//第二趟排序,就是将最小的数排在第一位
for (int j = 0; j < arr.length - 1 - 5; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temp;
System.out.println("最后一趟排序后的数组");
System.out.println(Arrays.toString(arr));
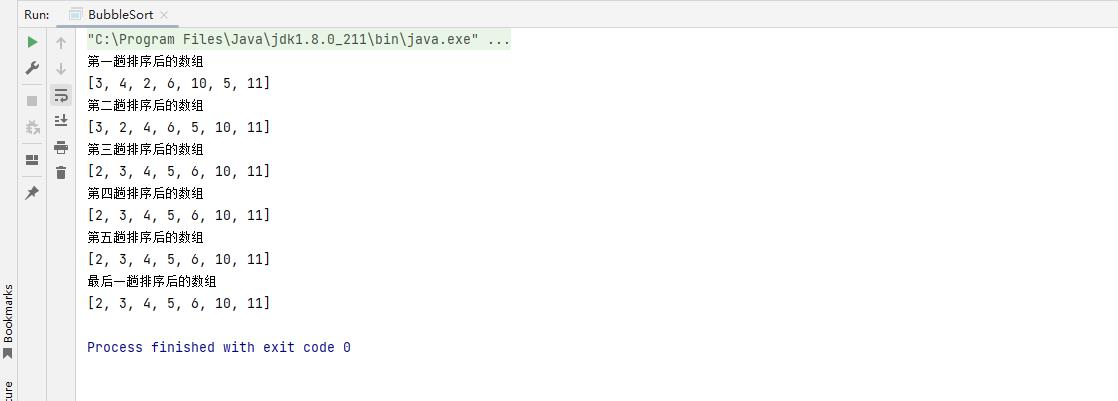
不知道大家看完六次排序的代码发现什么规律没有,分开写只是方便大家理解实际过程中只需要一个双重循环就可以解决代码冗余的问题。
public static void main(String[] args)
int arr[] = 3, 6, 4, 2, 11, 10, 5;
int temp = 0; //临时变量
for (int i=0; i< arr.length -1; i++)
for (int j = 0; j < arr.length - 1 -i; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
System.out.println("第"+(i+1)+"趟排序后的数组");
System.out.println(Arrays.toString(arr));
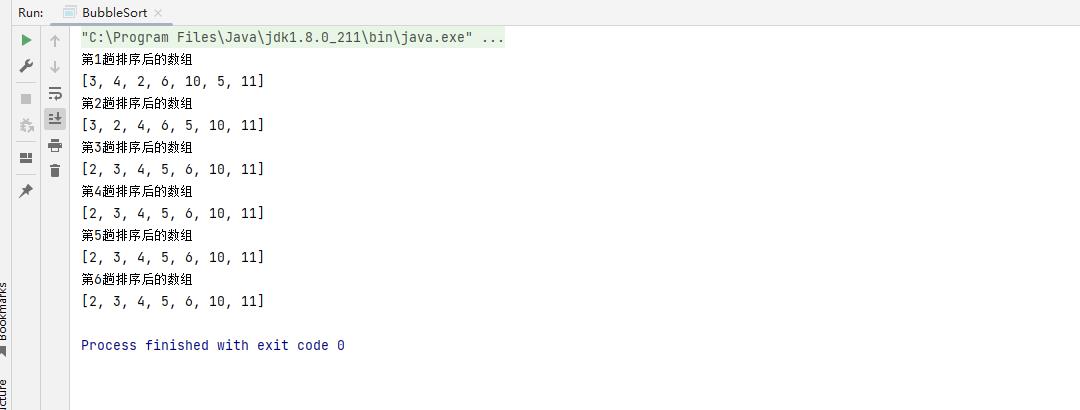
当进行六次排序后还有一位数还需不需要进行第七次排序了?答案是不需要,因为确定了六个数据的位置已经没必要知道第七个数据的位置了。对比上图,虽然我们最终的结果正确了,但是大家有么有发现在第三次排序之后已经成功了。后续的数据都是一样的结果,那么针对这种情况怎么优化呢?后面会给大家讲到!
排序优化
针对上面提出的情况怎么优化呢?因为排序的过程中,各元素不断接近自已的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。话不多说直接上代码!
public static void main(String[] args)
int arr[] = 3, 6, 4, 2, 11, 10, 5;
System.out.println("排序前");
System.out.println(Arrays.toString(arr));
//测试冒泡排序
bubbleSort(arr);
System.out.println("排序后");
System.out.println(Arrays.toString(arr));
public static void bubbleSort(int[] arr)
boolean flag = false; //标识变量,表示是否进行过交换
int temp = 0; //临时变量
for (int i=0; i< arr.length -1; i++)
for (int j = 0; j < arr.length - 1 -i; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
flag = true; //表示交换过
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
if (!flag) //在一趟排序中,一次交换都没有发生过
break;
else
flag = false; //重置flag,进行下次判断
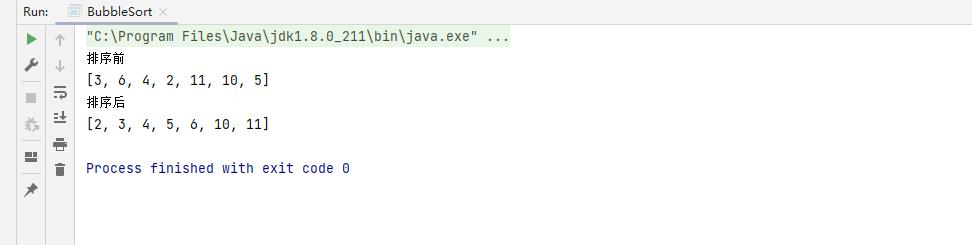
优化后的代码,在for循环的运行中没有进行交换就会走到break退出代码。
性能测试
冒泡排序的速度为O(n的二次方),假如我们给数据组加入80000条数据我们来测试一下冒泡排序的性能到底如何。
public static void main(String[] args)
// int arr[] = 3, 6, 4, 2, 11, 10, 5;
int arr[] = new int[80000];
for (int i = 0;i<arr.length;i++)
arr[i] = (int) (Math.random() * 8000000); //生成一个0-8000000的数
Date date1 = new Date();
SimpleDateFormat dateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String date1Str = dateFormat.format(date1);
System.out.println("排序前的时间为:"+date1Str);
//测试冒泡排序
bubbleSort(arr);
Date date2 = new Date();
String date2Str = dateFormat.format(date2);
System.out.println("排序后的时间为:"+date2Str);
public static void bubbleSort(int[] arr)
boolean flag = false; //标识变量,表示是否进行过交换
int temp = 0; //临时变量
for (int i=0; i< arr.length -1; i++)
for (int j = 0; j < arr.length - 1 -i; j++)
//如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
flag = true; //表示交换过
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
if (!flag) //在一趟排序中,一次交换都没有发生过
break;
else
flag = false; //重置flag,进行下次判断
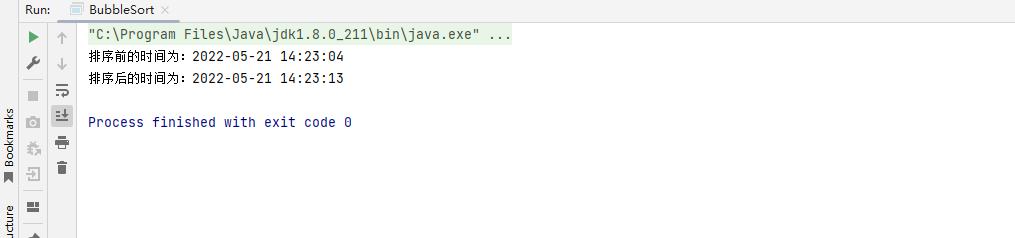
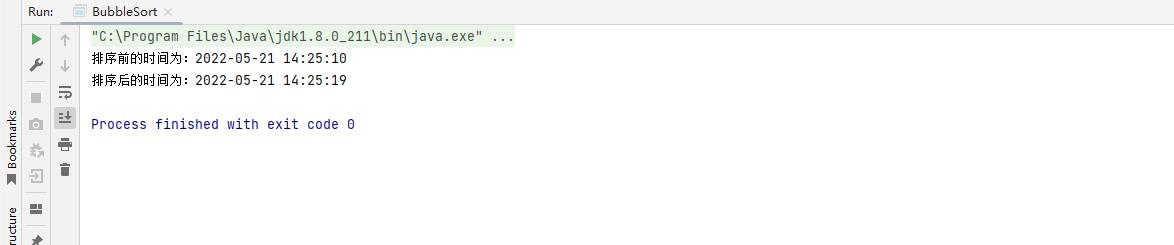
经过我们的多次执行,发现冒泡排序在处理八万条数据的时间大概为十秒左右由此可见冒泡排序的性能并不高!
以上是关于详解Java算法之冒泡排序(Bubble Sorting)的主要内容,如果未能解决你的问题,请参考以下文章