用MATLAB三步完成机器人搭建

Posted 2022-04-19 数据与算法之美

全世界只有3.14 % 的人关注了

爆炸吧知识

如果说机器人是一粒种子，那么《机器人大擂台》这档节目就是那个播种人。节目中，不同选手操纵着机器人，在擂台上各显神威 —— 冲撞、翻滚、撬杠、喷火等各种技能，总能令人眼花缭乱，同时点燃心中关于机器人的各种幻想。

图片来自 https://giphy.com/gifs/

‍如今的机器人应用广泛，机器人技术也开始源源不断地向人类活动的各个领域渗透，机器人分拣系统和随处可见的无人机。

例如机器人分拣系统，显著地提升了物流公司货物配送的效率：

另一个例子是无人机。如果说分拣机器人还属于各大物流公司的核心机密，如下凡天仙一般平日里难得一睹芳容，那无人机早已化身邻家女孩，平易近人地装点着我们的生活：

机器人的发展不会止步于此。2020年以来，新基建概念大热，其三大方向更是与机器人产业密切相关。教育机器人、送餐机器人、情感机器人及自动驾驶技术，都是机器人及自动化技术的下一个重要落地目标：

动图来自《美国国家地理》

银河补习班里有句经典台词：“我的孩子，上的是全世界最好的补习班，银河补习班。”今天，MATLAB就为你带来宇宙最强机器人补习班，手把手教你如何建造属于自己的机器人！ 

许多人认为 MATLAB 是数学或教育软件。事实上，MATLAB 最初被广泛采用是在控制工程领域，随后开发了多种技术领先的算法包和工具箱，并被全球各大高校广泛采纳为数学教育软件 [1]。即将进入机器人补习班的你，准备好了吗？

第一步：安装机器人工具箱

工欲善其事，必先利其器，我们首先需要安装 MATLAB 的机器人工具箱（Robotics System Toolbox）。我们既可以上MathWorks 官网 [2] 下载，又可以通过打开 MATLAB 主界面，单击“添加项”（Add-Ons） 选项进行操作。

然后在搜索栏中输入 “Robotics System Toolbox”，进入第一个搜索结果即可安装：

目前软件已更新至最新版本R2020a，增加更多功能，小伙伴可以尝试康康

操作完成后，打开 MATLAB 并输入

>> ver

如果能找到如下信息

Robotics System Toolbox       Version 2.x         (Rxxxxx)

那么恭喜，机器人工具箱已安装成功！

第二步：你想要什么样的机器人？建模是关键

我们要设计的第一个机器人，是一条可以自由转动的机械手臂。在 MATLAB 中，机械手臂由不同的连杆（Link）通过关节（Joint）拼接而成。依活动状态分，关节又可分为旋转型和平移型，其意义顾名思义 [2]：

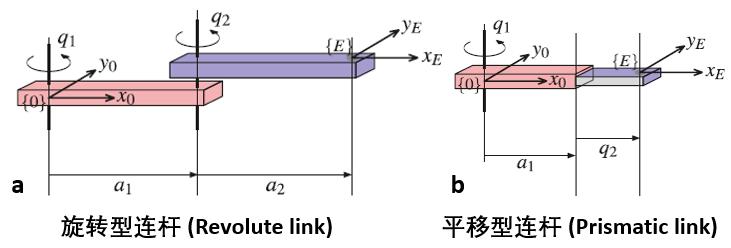
旋转型与平移型连杆

为简单起见，我们先创建一个三连杆的机械臂：

%设置 DH 参数dhparams = [0     pi/2  0     0;            0.4318  0       0       0;            ];
robot = rigidBodyTree; % 初始化机械臂body1 = rigidBody( body1 ); % 定义第一个连杆jnt1 = rigidBodyJoint( jnt1 , revolute ); % 定义第一个关节setFixedTransform(jnt1,dhparams(1,:), dh ); body1.Joint = jnt1; % 给底座加上关节addBody(robot,body1, base ) % 定义机械臂为机器人的底座
% 添加第二、三只连杆body2 = rigidBody( body2 ); jnt2 = rigidBodyJoint( jnt2 , revolute );body3 = rigidBody( body3 );jnt3 = rigidBodyJoint( jnt3 , revolute );setFixedTransform(jnt2,dhparams(2,:), dh );setFixedTransform(jnt3,dhparams(3,:), dh );body2.Joint = jnt2;body3.Joint = jnt3;

上面的 dhparams 是一个 n*4 矩阵（n 是机械臂的个数），被称为 DH 参数（Denavit–Hartenberg parameters）。dhparams 的每一行由 [a alpha d theta] 四个变量组成，它们分别表示：

• a: 关节（垂直连杆方向的）偏移量
  

• alpha: 关节扭曲角度（垂直于两个连杆构成的平面的角度）

• d: 关节（朝着连杆方向的）伸长量

• theta: 关节起始旋转角度（平行于两个连杆构成的平面的角度）

如果不小心忘了我们搭建的机器人长啥样，那么下面的命令 

showdetails(robot)

可以帮助我们回忆起它的基本特征：

而输入下面的命令，我们即可一睹该机械手臂的庐山真面目：

addBody(robot,body2, body1 )addBody(robot,body3, body2 )show(robot); % 画图

因为我们只搭建了最基本的连杆和关节，所以这个机械手臂难免有些瘦骨嶙峋。不过如果我们把上面的图片放大，就可以看到每个连杆、关节的名字、序号和类型具体信息：

此外，我们还可以给连杆和关节赋予诸如质量、转动惯量、惯性矩阵之类的参数，此处限于篇幅故略去之，有兴趣的小伙伴可以参考链接 [1] 或 [2]。实践出真知，理解以上概念最好的方式，就是逐个调整代码中的参数，观测结果变化。

第三步：看！它左手右手一个慢动作！

我们已经知道如何用 MATLAB 搭建一个简单的机器人了。然而这样搭建的机器人，和小朋友用积木搭建的玩具并无二致 —— 既然是用软件做成的机器人，我们自然希望它能动起来。我们以加拿大机器人公司 Kinova 的第三代机械臂为例，来看看 MATLAB 如何让这支麒麟臂动起来。

图片来自 https://www.kinovarobotics.com/en/products/gen3-robot

在 MATLAB 界面中输入

>> robot = loadrobot("kinovaGen3");>> showdetails(robot)

我们可以看到输出如下 

不难看出，第三代 Kinova 是由 8 根连杆和 8 个关节拼接而成。如果我们要想知道某个具体连杆的信息，例如名叫 “Shoulder_Link” 的连杆， 依次输入

>> robot.getBody( Shoulder_Link ).Joint>> robot.getBody( Shoulder_Link ).Joint.JointToParentTransform>> robot.getBody( Shoulder_Link ).Joint.ChildToJointTransform

即可分别查询属于该连杆的关节，以及关节到母连杆和子连杆的转移矩阵。如此一来，我们就可以从这种方法重建出第三代 Kinova 机械臂了！

现在我们有两种方法可以让让机械臂动起来。第一种方法是通过变换关节旋转角度的方式，这种方法叫正运动学（Forward kinematics）；第二种方法是通过给定每个连杆末端位置，这种方法叫逆运动学（Inverse kinematics）。正运动学可以很方便地对机械臂进行直接操控，而逆运动学则更有利于直接指定机械臂完成任务，例如抓取处于某位置的快递等等。这两种方法各有千秋。

有几何背景的读者知道，n 维欧式空间中的刚体形变可分为平移（Translation）、旋转（Rotation）和镜像（Reflection）三种，这三种变化可以用群作用，或者矩阵来表示。由这三种作用组成的群叫做欧几里得群（Euclidean Group）记作 E(n)，因为 E(n) 中的元素都可以用矩阵表示，所以 E(n) n+1 阶矩阵群的子群（具体解释见下图）。群 E(n) 中只由平移和旋转（不含镜像）构成的子群叫做特殊欧几里得群，记作 SE(n)。

下面我们 MATLAB 中的逆运动学函数 inverseKinematics 来让机械臂动起来。我们只需要定义出机械臂所要经过的几个路径点的位置、速度以及加速度，MATLAB 即可通过对特殊欧几里得群求逆来计算出整个机械臂所经过的路径，以及每个时刻的速度以及加速度等信息。

% 关节起始旋转角及初始位置positions = [2*pi, 0.2619, pi, 4.0142, 2*pi, 0.9598, pi/2];config = homeConfiguration(robot);for k = 1:length(positions)  config(k).JointPosition = positions(k);end
% 定义机械臂需要通过的路径点以及对应速度、加速度信息waypoints = [0.5639 0.0013 0.4336]  + [-0.1 0.2 0.4 ; -0.2 0 0.1 ; -0.1 -0.2 0.4 ;] ;waypointTimes = 0:4:8;ts = 0.2;trajTimes = 0:ts:waypointTimes(end);waypointVels = 0.1 *[ 0  1  0; -1  0  0; 0 -1  0;] ;waypointAccels = zeros(size(waypointVels));waypointAccelTimes = diff(waypointTimes)/4;[q,qd,qdd] = trapveltraj(waypoints,numel(trajTimes), ...             AccelTime ,repmat(waypointAccelTimes,[3 1]), ...              EndTime ,repmat(diff(waypointTimes),[3 1]));
% 画出初始状态%% 画图--机械臂show(gen3,config, Frames , off , PreservePlot ,false);hold on%% 画图--路径初始化hTraj = plot3(waypoints(1,1),waypoints(2,1),waypoints(3,1), b.- );set(hTraj,  xdata , q(1,:),  ydata , q(2,:),  zdata , q(3,:));%% 画图--路径点plot3(waypoints(1,:),waypoints(2,:),waypoints(3,:), ro , LineWidth ,2);set(gca,  Position , [-.2, -.2, 1.5, 1.5]);xlim([-1 1]), ylim([-1 1]), zlim([0 1.2]);

机械臂的初始位置。红色点表示机械臂所要经过的路径点

% 初始化机械臂的逆运动学方程ik = inverseKinematics( RigidBodyTree ,robot);ikWeights = [1 1 1 1 1 1];ikInitGuess = robot.homeConfiguration; % 随机设置一个初始状态
% 让机器人动起来！for idx = 1:numel(trajTimes)     % 解逆运动学方程    tgtPose = trvec2tform(q(:,idx) );    [config,info] = ik( EndEffector_Link , tgtPose,ikWeights,ikInitGuess);    ikInitGuess = config; % 以上一时刻的状态作为下一时刻的初始值
    % 画出机器人的动态    show(robot,config,  Frames , off , PreservePlot ,false);    title([  Trajectory at t =   num2str(trajTimes(idx))])    drawnow    end

最后得到的轨迹图如下：

有兴趣的读者可以修改上面代码中的参数（例如路径点的位置、机械臂的速度加速度等），来看看结果会出现怎样的变化。

更高级的智能

在实际使用中，除了要让机器人会动外，还需要赋予它们自主性。在本节中，我们希望机器人拥有路径规划以及障碍躲避的能力，让我们来一起见证什么是更高级的智能。

我们以即时定位与地图构建算法（Simultaneous localization and mapping，SLAM）作为例子。该算法可以通过著名的卡曼滤波（Kalman Filter）来得以实现。在如雷达、声呐、天气预报、火箭发射、计算机视觉、控制理论等诸多工程应用中，都离不开卡曼滤波的身影。

从抽象角度看来，卡曼滤波无非就是传感器不断根据外部环境，调控机器状态的一种装置。记机器状态 x （位置、速度等），传感器测量的外部环境变量为 z（温度、气压等），可调控的变量为 u （电磁波发射频率、前进方向等），v 和 w 分别表示机器和传感器误差，那么卡曼滤波可以表达为一个数学模型：

k 表示离散的时刻。如果 f 和 h 都是线性矩阵，那直接让上面两式对 x, z 分别求偏导数，然后再更新 x 和 z 的值即可（F_a, H_a 分别表示 f 和 h 对变量 a 的偏导数向量）：

如果 f 和 h 并非线性，由于误差项的累计，直接简单粗暴地线性化势必会带来更大的误差。为此，人们采用预测-更新（Predict-Update）两阶段算法来解决非线性的卡曼滤波问题 —— 在预测阶段，我们不仅要预测机器的状态 x，还要预测卡曼滤波的矩阵 P。这种算法叫扩展卡曼滤波（Extended Kalman Filter，EKF），是 SLAM 的灵魂所在，有兴趣的读者可参考文献 [2]。

P<k> 是卡曼滤波在时刻 k 的协方差矩阵，该矩阵在更新变量 x 时会起到作用

推导过程令人头秃？那我们来看一看代码及实现过程吧！

% 初始化机器人及起始点、终点% 我们的目的是希望机器人能顺利躲过障碍物并到达终点map = LandmarkMap(20, 10); % 10*10 地图，20 个障碍物V = diag([0.005, 0.5*pi/180].^2); % 机器（每个步长）的误差矩阵robot = Bicycle( covar , V); % 初始化机器人robot.add_driver( RandomPath(10)); % 定义终点% 定义传感器% angle：传感器扫射角度范围% range：传感器扫射距离W = diag([0.1, 1*pi/180].^2); % 传感器（每个步长）的误差矩阵sensor = RangeBearingSensor(robot, map,  covar , W, ...    animate ,  angle , [-pi/2 pi/2],  range , 5);
% 初始化 EKF， 并运行 150 个步长P0 = diag([0.005, 0.005, 0.001].^2); % 卡曼滤波初始时刻的协方差矩阵ekf = EKF(robot, V, P0, sensor, W, []);ekf.run(150);

上图中蓝色三角形表示机器人，红色菱形表示目标，粉红色扇形表示传感器扫查范围

造机器人？就是如此简单！

读到这里，相信大家对 MATLAB 的机器人工具包已经有了充足的认识。身边无人陪伴倍感孤独？—— MATLAB 帮你打造属于你自己的机器人！

机器人行业快速发展的同时，要面临各种各样的机遇和挑战。MATLAB 的机器人工具包也一样，仍需不断的革新和研发，在以下方面得以改善：

• 工具包没有覆盖机器视觉方面的内容，因此机器人的传感器只能处理非图像环境信息。要想给机器人加一双眼睛，需要下载计算机视觉工具箱（Computer Vision Toolbox）或图像处理工具箱（Image Processing Toolbox）；
  

• 工具包无法利用大数据，这在高度信息化的今天，对机器人的成长是不利的。要想让机器人拥有大数据处理技能，需要统计及机器学习工具箱（Statistics and Machine Learning Toolbox）或深度学习工具箱（Deep Learning Toolbox）。 

小时候在看《终结者》、《黑客帝国》等科幻电影时，总认为像“机器人三定律”这样的元素离真实世界还很遥远。然而随着计算机视觉、机器学习、深度学习等人工智能相关领域的迅速发展，这些科幻电影里的元素会离现实越来越近。小编希望这篇文章能对大家有所启发，真正的学习要从兴趣开始，而总有一天，你我会圆梦在今朝！ 

号外：5月28日北京时间13:30，线上技术研讨会（机器人与人工智能专题）：加速智能化融合，提高产品开发效率开播，感兴趣的小伙伴可以扫描二维码或点击阅读原文报名参与哟！

参考文献

[1]https://ww2.mathworks.cn/campaigns/products/trials.html?prodcode=RO&s_eid=PEP_23398

[2] https://ww2.mathworks.cn/products/robotics.html?s_eid=PEP_23398

[3] 蔡自兴, 谢斌. 《机器人学》. 清华大学出版社; 2000.

[4]https://www.mathworks.com/matlabcentral/fileexchange/71130-trajectory-planning-for-robot-manipulators