3d激光雷达开发（ransac的思想）

Posted 2022-03-17 费晓行

【 声明：版权所有，欢迎转载，请勿用于商业用途。 联系信箱：feixiaoxing @163.com】

        前面我们写了平面分割（https://blog.csdn.net/feixiaoxing/article/details/123388791?spm=1001.2014.3001.5501）、圆柱分割（https://blog.csdn.net/feixiaoxing/article/details/123389321?spm=1001.2014.3001.5501）这两篇文章。细心的同学可能发现，这里面都提到了ransac，那什么是ransac呢？

        所谓ransac，全称是random sample consensus，也就是随机采样一致性。名字听上去有点拗口，不妨举个例子来解释。假设一堆点云数据，我们怎么从中找到平面呢？一个简单的方法就是猜？随机找到几个点，算出一个平面，然后计算每个点距离这个平面的距离。继续撒点，如果发现新的点比原来的好，也就是其他点距离平面距离更小，那么更新老的点；否则继续寻找。这个里面，其实做了两个假设，一个假设是我们撒的点正好就在平面上，一个假设是只要样本多，总能找到合适的点。

        网上有一些说明这个原理的文章，部分还提供了代码，比如这一篇，https://zhuanlan.zhihu.com/p/62238520，读起来很是不错。

1、原来的代码有几处bug，修复了一下，

        1.1 i和iters的比较修改为while i < iters:

        1.2 添加i  += 1

        1.3 修正sigma=3，主要是为了提高运行速度，不用等太久

        1.4 添加try-except，防止出现除0异常

        1.5 添加UTF-8，不然中文过不了

2、修改后的代码如下所示，

#!/usr/bin/python
# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import random
import math

# 数据量。
SIZE = 50
# 产生数据。np.linspace 返回一个一维数组，SIZE指定数组长度。
# 数组最小值是0，最大值是10。所有元素间隔相等。
X = np.linspace(0, 10, SIZE)
Y = 3 * X + 10

fig = plt.figure()
# 画图区域分成1行1列。选择第一块区域。
ax1 = fig.add_subplot(1,1, 1)
# 标题
ax1.set_title("RANSAC")


# 让散点图的数据更加随机并且添加一些噪声。
random_x = []
random_y = []
# 添加直线随机噪声
for i in range(SIZE):
    random_x.append(X[i] + random.uniform(-0.5, 0.5)) 
    random_y.append(Y[i] + random.uniform(-0.5, 0.5)) 
# 添加随机噪声
for i in range(SIZE):
    random_x.append(random.uniform(0,10))
    random_y.append(random.uniform(10,40))
RANDOM_X = np.array(random_x) # 散点图的横轴。
RANDOM_Y = np.array(random_y) # 散点图的纵轴。

# 画散点图。
ax1.scatter(RANDOM_X, RANDOM_Y)
# 横轴名称。
ax1.set_xlabel("x")
# 纵轴名称。
ax1.set_ylabel("y")

# 使用RANSAC算法估算模型
# 迭代最大次数，每次得到更好的估计会优化iters的数值
iters = 100000
# 数据和模型之间可接受的差值
sigma = 3
# 最好模型的参数估计和内点数目
best_a = 0
best_b = 0
pretotal = 0
# 希望的得到正确模型的概率
P = 0.99
i = 0
while i < iters:

	# i += 1
    i += 1

    # 随机在数据中红选出两个点去求解模型
    sample_index = random.sample(range(SIZE * 2),2)
    x_1 = RANDOM_X[sample_index[0]]
    x_2 = RANDOM_X[sample_index[1]]
    y_1 = RANDOM_Y[sample_index[0]]
    y_2 = RANDOM_Y[sample_index[1]]

    # y = ax + b 求解出a，b
    a = (y_2 - y_1) / (x_2 - x_1)
    b = y_1 - a * x_1

    # 算出内点数目
    total_inlier = 0
    for index in range(SIZE * 2):
        y_estimate = a * RANDOM_X[index] + b
        if abs(y_estimate - RANDOM_Y[index]) < sigma:
            total_inlier = total_inlier + 1

    # 判断当前的模型是否比之前估算的模型好
    if total_inlier > pretotal:
        try:
            iters = math.log(1 - P) / math.log(1 - pow(total_inlier / (SIZE * 2), 2))
        except ZeroDivisionError:
            pass
			
        pretotal = total_inlier
        best_a = a
        best_b = b

    # 判断是否当前模型已经符合超过一半的点
    if total_inlier > SIZE:
        break

# 用我们得到的最佳估计画图
Y = best_a * RANDOM_X + best_b

# 直线图
ax1.plot(RANDOM_X, Y)
text = "best_a = " + str(best_a) + "\\nbest_b = " + str(best_b)
plt.text(5,10, text,
         fontdict='size': 8, 'color': 'r')
plt.show()

3、实际效果

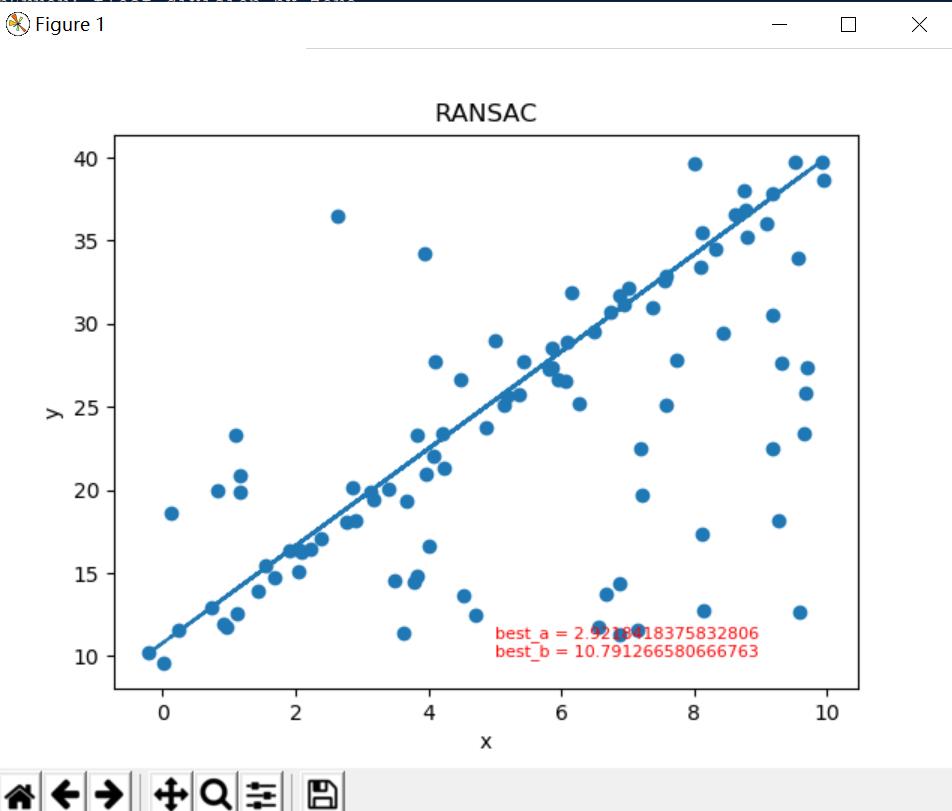
        代码没有修改之前，可能会出现除0错误，而且执行时间很长，有差不多10几秒钟，修改后可以短时间快速出结果。

4、最有意思的更新

    # 判断当前的模型是否比之前估算的模型好
    if total_inlier > pretotal:
        try:
            iters = math.log(1 - P) / math.log(1 - pow(total_inlier / (SIZE * 2), 2))
        except ZeroDivisionError:
            pass
			
        pretotal = total_inlier
        best_a = a
        best_b = b

        对iters的重新计算是最有意思的，实际效果也许有限。注意虽然SIZE是50，但是实际random_x、random_y的大小是100，所以这里乘以2。此外后面一个2，代表每次只需取两个点即可，所以N=2。其他部分和k=log（1-P)/log(1-t的N次方)这个公式是完全匹配的。