深度学习+强化学习=深度强化学习
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习+强化学习=深度强化学习相关的知识,希望对你有一定的参考价值。
- 作者: 自硕21 陈昱宏
§01 深度学习
深度学习(Deep Learning,DL)是机器学习的一个热门研究领域,是一种对数据进行表征学习的方法,目前已经在图像识别、语音辨识、自然语言处理等领域,获得了显著的成果。DL的基本思想是堆叠多层系统,对输入的信息进行分级处理,再透过调整系统中的参数,让输出的结果与输入的差别尽可能的小。
深度学习的概念来自于人工神经网络,例如含有多隐层的多层感知器,就是深度学习一个很典型的结构。深度学习的目标是透过低层次的特征构成高层次的特征,进而学习特征结构,在多个抽象的特征上,让智能体自动学习将输入的信息数据,映射到输出数据的复杂功能,以获得与输入数据差异最小的输出结果,而不需要仰赖人工制造的功能。例如在文献[1]中,作者利用深度学习的技术,将输入的图像透过多层神经网络进行语义分析,当智能体获得一张图片输入时,会先将图片分解成许多像素,透过各个像素中所出现的特征,经过多层的神经网络,得到整张图片的特征。
在深度学习领域一般使用神经网络模型对问题建模求解,其中以卷积神经网络(Convolutional Neural Networks, CNN)最为著名。卷积神经网络时一垒包含卷积计算且具有深度结构的前馈神经网络,而卷积神经网络的雏形是来源于1998年著名科学家Yann LeCun提出了LeNet-5[2],将BP算法应用导神经网络结构的训练上。一直到2012年,AlexNet网络[3] 出现之后,神经网络开始崭露头角,在该文中AlexNet引入了全新的深层结构和dropout方法,将错误率从25%提升到了15%。在2015年,Oxford的Visual Geometry Group提出了基于AlexNet改进的VGG网络[4],采用连续的几个3×3的卷积核代替AlexNet中的较大卷积核(11×11,7×7,5×5),利用感受野的概念使用较少的参数去保证学习更复杂的模式。同年,微软研究院的何恺明、张祥雨、任少卿、孙剑等人,提出了残差神经网络(ResNet)[5],在网络中添加残差结构,使得神经网络的性能不会出现退化现象,更好的提升了图像识别的准确率。
在近几年的发展,越来越多神经网络被提出并优化,但有些问题不能仅仅靠着深度学习解决,还需要结合强化学习来对问题建模求解。
§02 强化学习
强化学习(Reinforcement Learning,RL),作为另一个机器学习重要的研究领域,是一种让智能体透过选择不同的行为,来获取最大的奖励信号的学习方法,在工业制造、游戏博弈、机器人控制等领域,有着广泛的应用。强化学习的基本思想,是让智能体从环境中获取一种状态,由智能体进行决策,对环境作出一种行为,再由环境反馈奖励信号给智能体,透过多次的上述过程,智能体由过往的经历,学习获得的奖励信号最佳的行为。
强化学习借由智能体与环境的交互过程,对于不同的行为给予一定的奖励,训练智能体选择做出获得最大奖励函数的行为。如图1所示,环境会给予智能体一个状态,智能体根据自身策略选择一种行为在环境中操作,环境根据不同的行为,返回给相应的奖励函数和新的状态,经过多次的交互过程后,智能体会学习到一个较好的行为策略,从而获得更大的奖励,因此在强化学习中,如何设计奖励函数,显得尤为重要,一些可能影响学习策略的先验知识,都是必须考虑如何在奖励函数的设计中体现[6]。
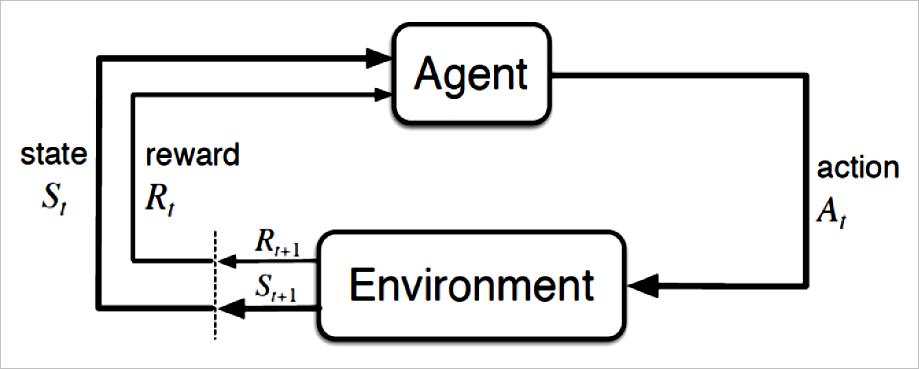
▲ 图2.1 强化学习基本概念
然而,随着人工智能需要处理的情境越来越复杂,谷歌的人工智能团队—DeepMind提出了创新性的概念,将对感知信号处理的深度学习与进行决策处理的强化学习相结合,形成所谓的深度强化学习(Deep Reinforcement Learning,DRL),利用深度强化学习可以解决以前强化学习难以处理的问题。传统的强化学习算法虽然已经尽可能的模拟了人在学习事情的过程,但是依然会遇到一些无法处理的问题,主要是环境状态的改变与智能体所做的行为有关,两者间可能含有强烈的时间相关性,如果不使用深度学习的算法,容易造成智能体的行为策略难以收敛或是不稳定,此外如果一个行为的后果,需要经过一段时间的过程才会实现,例如信用分配问题,也容易造成智能体在训练过程的不稳定[7]。
§03 深度强化学习
(一)深度强化学习简介
人工智能领域中,所追求的是制造出通用在各个领域的人工智能,但在各个领域所遇到的环境可能有很大的差别,而人工智能的想法是用计算机去模拟人的大脑来处理事情,所以人工智能需要模拟人在学习各个领域知识的过程,进而创造出能通用的人工智能。
那么,人是如何学习的呢?人在婴儿时期的学习过程,会先观察遇到的情况,在尝试性地做出一个行为,透过不断的尝试,来试探大人的反应,以及是否会得到奖励(如:糖果),在这样的过程学习一个可以让自己免于受处罚又可获得奖励的行为,为了模拟人的学习,因此产生了新的机器学习方法—深度强化学习。
深度强化学习是一个结合深度学习和强化学习的新概念,然而,深度强化学习究竟和强化学习有什麼區別呢?深度强化学习是让智能体自己去观察环境的状态,借由深度学习的感知处理,让智能体能够学习观察环境状态的特征,接着再借由强化学习的决策训练,完成整个深度强化学习的结构;强化学习则是由环境直接告诉智能体现在的状态,不需要智能体自己去观察,然后智能体接着开始学习如何做决策。
因为现在环境的状态越来越复杂,在如此复杂的情况底下,让智能体透过深度学习的多层神经网络,自己去学习观察状态的表征,依照观察出来的表征再透过强化学习的结构,自己优化解决问题时的策略,这也就是深度学习的核心想法。
(二)深度强化学习基本数学建模
在深度强化学习中,主要的核心还是在于强化学习的基础,透过深度学习抽取特征和函数复杂映射的能力,将强化学习中的一些痛点加以解决。在强化学习中,主要是希望智能体学习一种行为策略,能够根据当前环境信息对应的输出一个行为:
a = π ( s ) a = \\pi \\left( s \\right) a=π(s)
其中𝑎是动作,𝑠则是智能体在环境中的状态。根据不同的环境,动作和状态可能是离散或是连续的。
强化学习的问题可以被建模成一个马尔可夫决策过程[8],马尔可夫过程的特点是一个系统中,下一个时刻的状态仅跟当前状态有关,与之前的状态无关;而马尔可夫决策过程则是指下一时刻的状态由当前状态和当前时刻的动作决定。马尔可夫决策过程可以用一个五元组表示:
S , A , P a , R a , γ \\left\\ S,A,P_a ,R_a ,\\gamma \\right\\ S,A,Pa,Ra,γ
在这个五元组中,𝑆代表着状态空间,𝐴代表着动作空间,𝑃𝑎代表着状态转移的概率,一般用来描述执行一个动作后从当前状态转移到下一个状态的概率,𝑅𝑎代表着当前状态执行了一个动作后的奖励,𝛾是折现因子,用来将未来获得的奖励折扣到当前时刻的奖励中。用数学的表达式可以表示𝑃𝑎和𝑅𝑎:
P
a
(
s
t
=
s
0
,
s
t
+
1
=
s
1
)
=
p
(
s
t
+
1
=
s
1
∣
s
t
=
s
0
,
a
t
=
a
)
P_a \\left( s_t = s_0 ,s_t + 1 = s_1 \\right) = p\\left( s_t + 1 = s_1 |s_t = s_0 ,a_t = a \\right)
Pa(st=s0,st+1=s1)=p(st+1=s1∣st=s0,at=a)
R
a
(
s
0
)
=
E
[
r
t
∣
s
t
=
s
0
,
a
t
=
a
]
R_a \\left( s_0 \\right) = E\\left[ r_t |s_t = s_0 ,a_t = a \\right]
Ra(s0)=E[rt∣st=s0,at=a]
马尔可夫决策过程要解决的核心问题就是选择动作的策略,在数学上使用𝜋函数来表示:
π
(
a
∣
s
0
)
=
p
(
a
t
=
a
∣
s
t
=
s
0
)
\\pi \\left( a|s_0 \\right) = p\\left( a_t = a|s_t = s_0 \\right)
π(a∣s0)=p(at=a∣st=s0)
在奖励上,我们要考虑的是当前状态下的总回报,从模型上来说,将来奖励的不确定性大,不能够简单的将未来奖励直接加总;从数学上来说,需要满足级数收敛的问题。因此,需要透过一个折现因子将未来每个时刻的期望奖励折现到当前时刻:
g
t
=
r
t
+
γ
r
t
+
1
+
γ
2
r
t
+
2
+
⋯
=
∑
k
=
0
∞
γ
k
r
t
+
k
g_t = r_t + \\gamma r_t + 1 + \\gamma ^2 r_t + 2 + \\cdots = \\sum\\limits_k = 0^\\infty \\gamma ^k r_t + k
gt=深度强化学习的实操 动作空间状态空间回报函数的设计以及算法选择训练调试和性能冲刺
深度强化学习的实操 动作空间状态空间回报函数的设计以及算法选择训练调试和性能冲刺