边缘检测---多尺度 (金字塔+BEMD+小波分析)
Posted 鼠标滑轮不会动
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了边缘检测---多尺度 (金字塔+BEMD+小波分析)相关的知识,希望对你有一定的参考价值。
🙋♂️写在最前面的
- 🥳博客主页:😋 鼠标滑轮不会动 😋
- 🏅欢迎 关注🎯 点赞👍 收藏⭐️ 留言📋
- 🎬首发时间:🎉2022年1月4日🎉
- 🆕最新更新时间:🎉2021年1月5日🎉
- 🌟本文由 鼠标滑轮不会动 原创,CSDN首发!
- 📬黑夜给了黑色的眼睛,我却用它来寻找光明!
- 📌本人水平非常有限,如有错误,请留言捶我小脑袋,万分感谢!
目录
-
热门文章推荐
-
☑️跑通代码—CVPR2020–StegaStamp: Invisible Hyperlinks in Physical Photographs
-
☑️跑通代码—WACV2020-Dense Extreme Inception Network: Towards a Robust CNN Model for Edge Detection
-
☑️跑通代码—ICCV2021-HiNet: Deep Image Hiding by Invertible Network
-
☑️代码复现—2021-IEEE-TETCI-A Generalized Deep Neural Network Approach for Digital Watermarking Analysis

✨前言
图像的边缘检测是计算机视觉中的一项基础任务。很多工作都使用了多尺度的边缘提取方法,本文总结了三种传统的多尺度边缘提取方法,并使用MATLAB软件做了三个小实验,展示和分析的对应实验的边缘的效果。
✨多尺度—图像金字塔
图像金字塔分解能够得到不同尺度的图像,从而在多尺度下提取更加丰富的边缘信息。采用的办法是Laplacian of Gaussian(LoG) 去构建图像的尺度空间。
上图为不同尺度下的Lena图像,不同尺度的图像包含的细节信息不同,尺度越小包含的信息越多,图像的边缘和纹理更加的丰富。小尺度边缘图像细节丰富,但主要边缘特征被淹没,且包含较多噪声; 大尺度边缘图像保留了图像的主要边缘且噪声较少,但边缘定位不准确。
🌿基于图像金字塔的边缘检测
穆柯楠1提出一种基于非采样高斯差分金字塔的边缘检测算法。使用的多尺度融合的方法,但是融合之后的还是单像素边缘。融合的思想很简单,原始尺度的边缘中点在下一个尺度的3×3邻域内还是边缘点就记录下来,不断更新所有尺度的边缘点信息,得到的边缘点信息设置阈值删除长度较短的边缘,得到最终的边缘图像,阈值选取根据实验结果。
穆柯楠论文中有用的点: 介绍了两种图像边缘检测性能的计算公式,分别是Abdou-Pratt 品质因数和连续度的计算。Abdou-Pratt 品质因数用来判断边缘检测算法对噪声的容忍度及边缘检测的精确度。 F = 1 max ( N a , N d ) ∑ i = 1 N d 1 1 + a × d i 2 F=\\frac1\\max \\left(N_\\mathrma, N_\\mathrmd\\right) \\sum_i=1^N_\\mathrmd \\frac11+a \\times d_i^2 F=max(Na,Nd)1i=1∑Nd1+a×di21其中 N a N_a Na 和 N d N_d Nd 分别为实际边缘数和检测到的边缘数; d i d_i di 表示检测到的第 i i i 条边缘对 应的实际边缘的距离; a a a 为常系数, 取 a = 1 / 9 。 F a=1 / 9 。F a=1/9。F 值越大, 表明边缘点的定位精度越高. f ( C i ) = 2 × ( 1 1 + exp ( − C i / α ) − 0.5 ) C = ∑ i = 1 m ( n i f ( C i ) / ∑ i = 1 m n i ) \\beginarrayr f\\left(C^i\\right)=2 \\times\\left(\\frac11+\\exp \\left(-C^i / \\alpha\\right)-0.5\\right) \\\\ C=\\sum_i=1^m\\left(n_i f\\left(C^i\\right) / \\sum_i=1^m n_i\\right) \\endarray f(Ci)=2×(1+exp(−Ci/α)1−0.5)C=∑i=1m(nif(Ci)/∑i=1mni) α = min ( n , m ) / 20 \\alpha=\\min (n, m) / 20 α=min(n,m)/20 时能较好满要求, m m m 为边缘图像 E E E 中的边缘段数量, n n n 为边缘像素数量。 C C C越接近1表示边缘图像的连续性越好。
🌿自己的实验—金字塔+Canny
对于多尺度融合,我考虑对比使用金字塔前后的不同。具体的做法是将图像多尺度分解为3层,每层有3个不同的高斯滤波核进行滤波,图像的尺寸逐层减小。对三个不同过的层分别进行Canny边缘检测,将检测结果的图像重新恢复到最初尺寸 512 × 512 512×512 512×512,并使用加权的方式,设置不同层的权重,认为初始层的权重最小,最后一层的权重最大,设置的理由是尺度小的细节信息保留的较少,更能代表图像不随尺度变化的边缘信息,所以权重更大,尺度大的图像纹理信息太多,权重少一些。
上图为不同尺度下的Lena图像,不同尺度的图像包含的细节信息不同,尺度越小包含的信息越多,图像的边缘和纹理更加的丰富。小尺度边缘图像细节丰富,但主要边缘特征被淹没,且包含较多噪声; 大尺度边缘图像保留了图像的主要边缘且噪声较少,但边缘定位不准确。
✨多尺度—二维经验模态分解
🌿BEMD算法简介
BEMD 算法是一种基于数据的局部时间特征尺度分析非线性和非稳态数据的方法, 广泛应用于非线性和非平稳过程2. 由于BEMD算法的步骤已经很成熟固定,本文不再赘述,具体参见文献3.
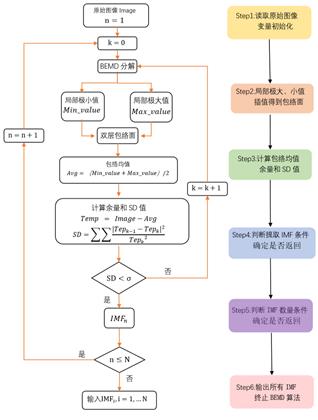
S t e p 1 : Step1: Step1: 读取图像Image, 对变量进行初始化 n = 1 , k = 0 n=1, k=0 n=1,k=0.
S t e p 2 : Step2: Step2: 求图像Image 的局部极大值 (Max value) 和极小值 (Min value). 使用揷值方 法得到曲面的包络(不同揷值方法对应 IMF 结果有差异)
S t e p 3 : Step3: Step3: 计算包络均值 A v g = ( A v g=\\left(\\right. Avg=( Max value − - − Min value ) / 2 \\left._\\text value \\right) / 2 value )/2 和终止判断条件
S D = ∑ ∑ ∣ T e m p k − 1 − T e m p k ∣ 2 T e m p k 2 , \\mathrmSD=\\sum \\sum \\frac\\left|T e m p_k-1-T e m p_k\\right|^2T e m p_k ^2, SD=∑∑Tempk2∣Tempk−1−Tempk∣2,
其中, Temp = = = Image − - − Avg .
S t e p 4 : Step4: Step4: 判断SD ≤ σ \\leq \\sigma ≤σ, 如果成立, 得到第 n n n 个IMF, 记为 I M F n I M F_n IMFn, 然后判断 n ≤ N \\mathrmn \\leq \\mathrmN n≤N, 如果是, 令Image = = = Temp, n = n + 1 n=n+1 n=n+1, 重复步骤 (2) 和 (3), 如果否, 结束算 法, 输出 I M F i , i = 1 , 2 , … , n \\mathrmIMF_i, i=1,2, \\ldots, \\mathrmn IMFi,i=1,2,…,n; 如果不成立, 令Image = = = Temp, 重复步骤 S t e p 2 − S t e p 3 Step2-Step3 Step2−Step3. 其中, σ \\sigma σ 为事先选定的阈值4, 一般取值范围为 0.2 ∼ 0.3 0.2 \\sim 0.3 0.2∼0.3.
于是, 便可以得到分解的结果.
Image = ∑ i = 1 n − 1 I M F i + residue ( I M F n ) . \\text Image =\\sum_i=1^n-1 I M F_i+\\text residue \\以上是关于边缘检测---多尺度 (金字塔+BEMD+小波分析)的主要内容,如果未能解决你的问题,请参考以下文章