机器学习--线性回归算法的原理及优缺点

Posted 2020-11-16 lsm-boke

一、线性回归算法的原理

　　回归是基于已有数据对新的数据进行预测，比如预测股票走势。这里我们主要讲简单线性回归。基于标准的线性回归，可以扩展出更多的线性回归算法。　

                                             

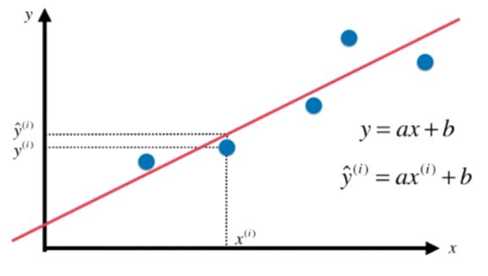
 　　假设我们找到了最佳拟合的直线方程 ： ，

　　　　则对每一个样本点    ，根据我们的直线方程，预测值为：，其对应的真值为   。

　　我们希望    和   的差距尽量小，这里我们用   表达   和  的距离，

　　　　考虑所有样本则为：

　　我们的目标是使   尽可能小，而    ，所以我们要找到  a 、b  ,使得  尽可能小。

　　　　被称为损失函数或效用函数。

　　通过分析问题，确定问题的损失函数或效用函数，通过最优化损失函数或者效用函数，获得机器学习的模型，这是参数学习算法的一半套路。

　　求损失函数可转化为典型的最小二乘法问题: 最小化误差的平方。

　　　　最小二乘法的求解过程：

                   目标：找到  a 、b  ,使得  尽可能小。

　　　　　　  

　　　　　　     

　　　　　　 

 　　　　　　　　　　　　    

　　　　　　　　　　     

　　　　　　　　　　　       

　　　　　      　　　　　  

　　　　　　　　　　　        

　　　　             

　　　　　　　　　　　　          

　　　　　　　　　　　　                    

　　　　　　　　　　　　　　  

　　　　　　　　　　　　　　　             

　　　　　　　　　　　　　　　　　  

　　　　　　　　　　　 

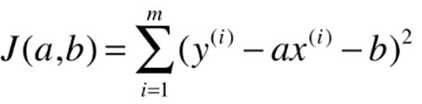
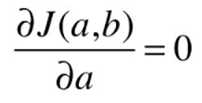
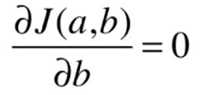
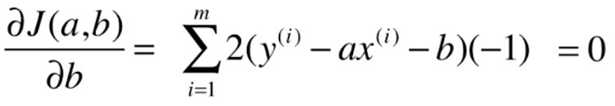
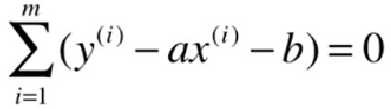
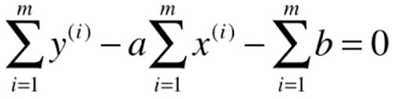
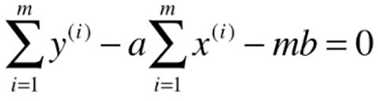
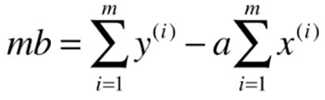
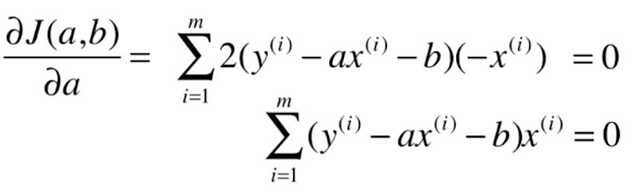
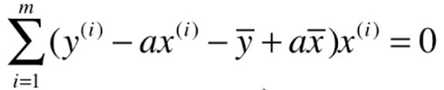
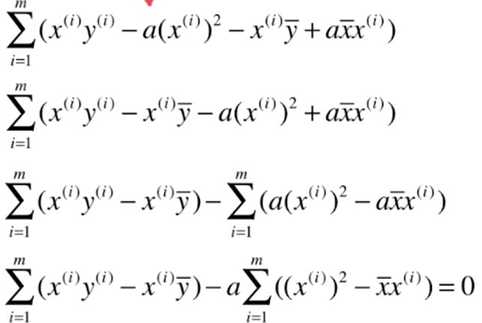
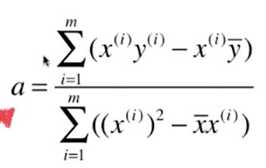
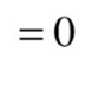
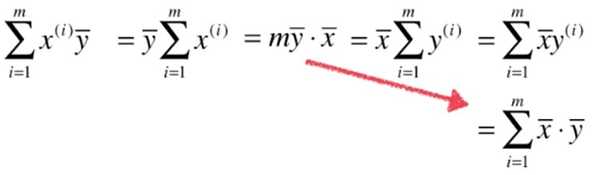
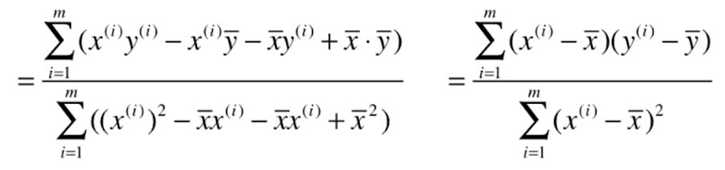
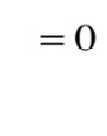
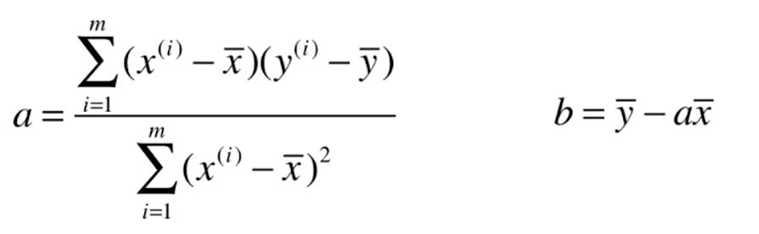
　　一般过程：

               假设输入数据集D有n个样本，d个特征，则：
                         
              其中第个样本表示为：
                         
              线性模型通过建立线性组合进行预测。我们的假设函数为：
                          
                                   其中为模型参数。
              令，为行向量，令
                               
                              为维矩阵,为维向量，则假设函数(1)式可表示为：
                                                                   
                             损失函数为均方误差，即
                                            
                           最小二乘法求解参数，损失函数对求导：
                                                  
                           令，得

                                                            

 

二、算法优缺点

　　优点：

　　　　（1）思想简单，实现容易。建模迅速，对于小数据量、简单的关系很有效；

　　　　（2）是许多强大的非线性模型的基础。

　　　　（3）线性回归模型十分容易理解，结果具有很好的可解释性，有利于决策分析。

　　　　（4）蕴含机器学习中的很多重要思想。

　　　　（5）能解决回归问题。

　　缺点：

　　　　（1）对于非线性数据或者数据特征间具有相关性多项式回归难以建模.

　　　　（2）难以很好地表达高度复杂的数据。

三、代码实现

　　1.简单的线性回归算法

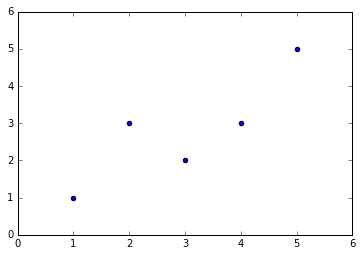
import numpy as np
import matplotlib.pyplot as plt

x=np.array([1,2,3,4,5],dtype=np.float)
y=np.array([1,3.0,2,3,5])
plt.scatter(x,y)

x_mean=np.mean(x)
y_mean=np.mean(y)
num=0.0
d=0.0
for x_i,y_i in zip(x,y):
    num+=(x_i-x_mean)*(y_i-y_mean)
    d+=(x_i-x_mean)**2
    a=num/d
    b=y_mean-a*x_mean
y_hat=a*x+b

plt.figure(2)
plt.scatter(x,y)
plt.plot(x,y_hat,c=‘r‘)
x_predict=4.8
y_predict=a*x_predict+b
print(y_predict)
plt.scatter(x_predict,y_predict,c=‘b‘,marker=‘+‘)

  输出结果：

                          

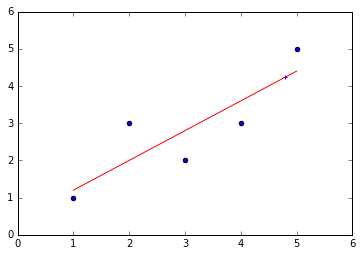
　　2.基于sklearn的简单线性回归

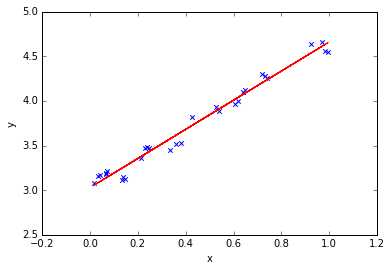
import numpy as np 
import matplotlib.pyplot as plt  
from sklearn.linear_model import LinearRegression  # 线性回归


# 样本数据集，第一列为x，第二列为y，在x和y之间建立回归模型
data=[
    [0.067732,3.176513],[0.427810,3.816464],[0.995731,4.550095],[0.738336,4.256571],[0.981083,4.560815],
    [0.526171,3.929515],[0.378887,3.526170],[0.033859,3.156393],[0.132791,3.110301],[0.138306,3.149813],
    [0.247809,3.476346],[0.648270,4.119688],[0.731209,4.282233],[0.236833,3.486582],[0.969788,4.655492],
    [0.607492,3.965162],[0.358622,3.514900],[0.147846,3.125947],[0.637820,4.094115],[0.230372,3.476039],
    [0.070237,3.210610],[0.067154,3.190612],[0.925577,4.631504],[0.717733,4.295890],[0.015371,3.085028],
    [0.335070,3.448080],[0.040486,3.167440],[0.212575,3.364266],[0.617218,3.993482],[0.541196,3.891471]
]


#生成X和y矩阵
dataMat = np.array(data)
X = dataMat[:,0:1]   # 变量x
y = dataMat[:,1]   #变量y


# ========线性回归========
model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.fit(X, y)   # 线性回归建模
print(‘系数矩阵:
‘,model.coef_)
print(‘线性回归模型:
‘,model)
# 使用模型预测
predicted = model.predict(X)

plt.scatter(X, y, marker=‘x‘)
plt.plot(X, predicted,c=‘r‘)

plt.xlabel("x")
plt.ylabel("y")

输出结果：

     系数矩阵:
     [ 1.6314263]
    线性回归模型:
     LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)