ccc-pytorch-LSTM
Posted 扔出去的回旋镖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ccc-pytorch-LSTM相关的知识,希望对你有一定的参考价值。
文章目录
一、LSTM简介
LSTM(long short-term memory)长短期记忆网络,RNN的改进,克服了RNN中“记忆低下”的问题。通过“门”结构实现信息的添加和移除,通过记忆元将序列处理过程中的相关信息一直传递下去,经典结构如下:
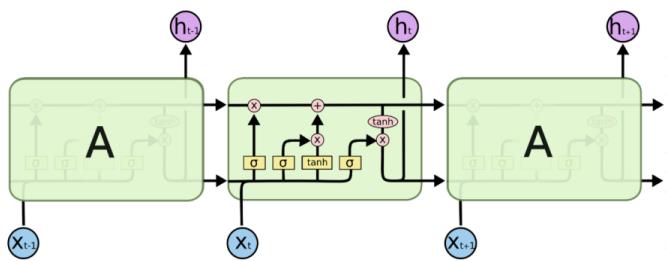

二、LSTM中的核心结构
记忆元(memory cell)-长期记忆:
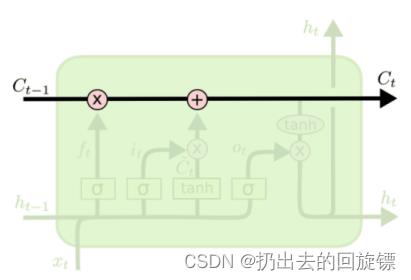
就像一个cell一样,信息通过这条只有少量线性交互的线传递。传递过程中有3种“门”结构可以告诉它该学习或者保存哪些信息
三个门结构-短期记忆
遗忘门:用来决定当前状态哪些信息被移除
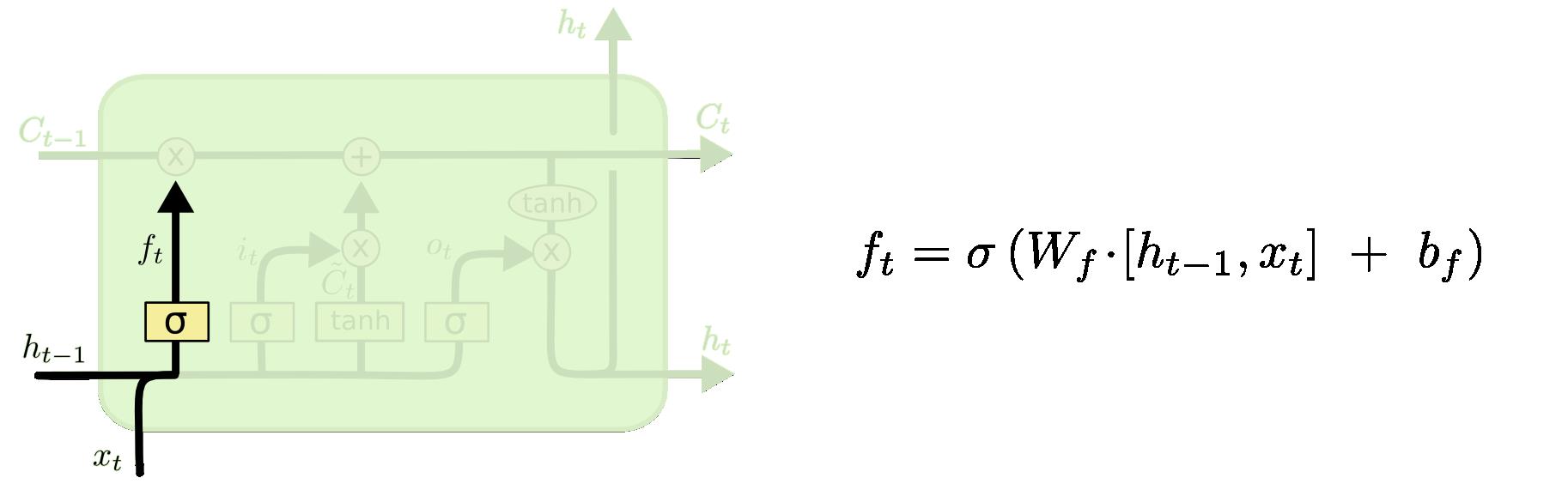
输入门:决定放入哪些信息到细胞状态
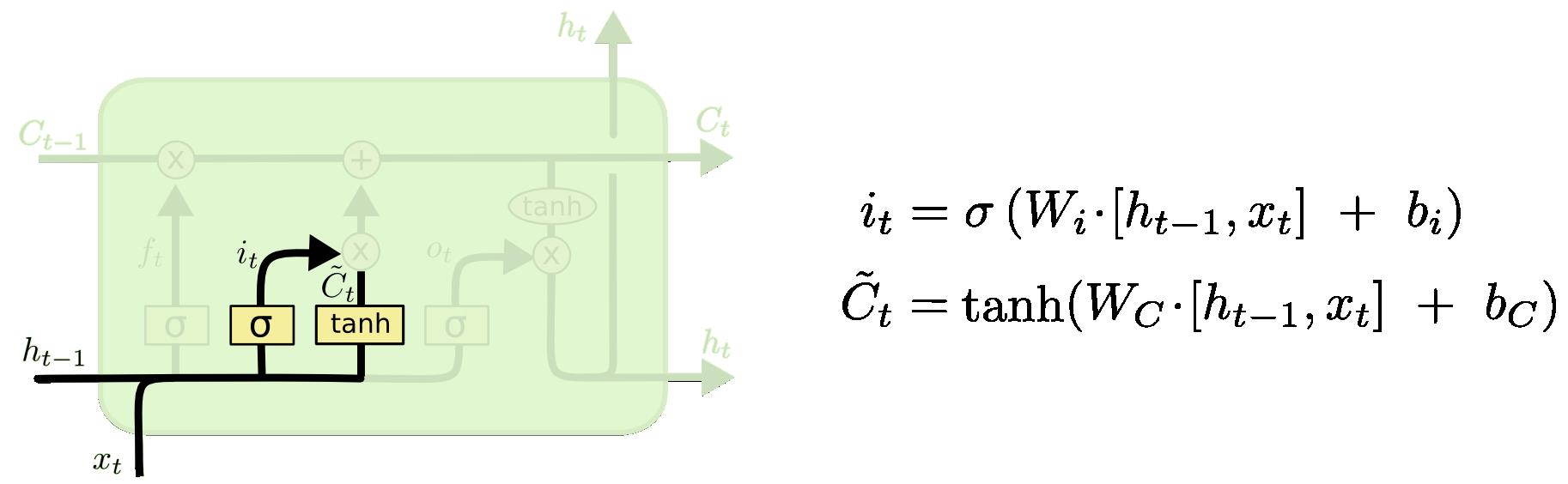
输出门:决定哪些信息用于输出
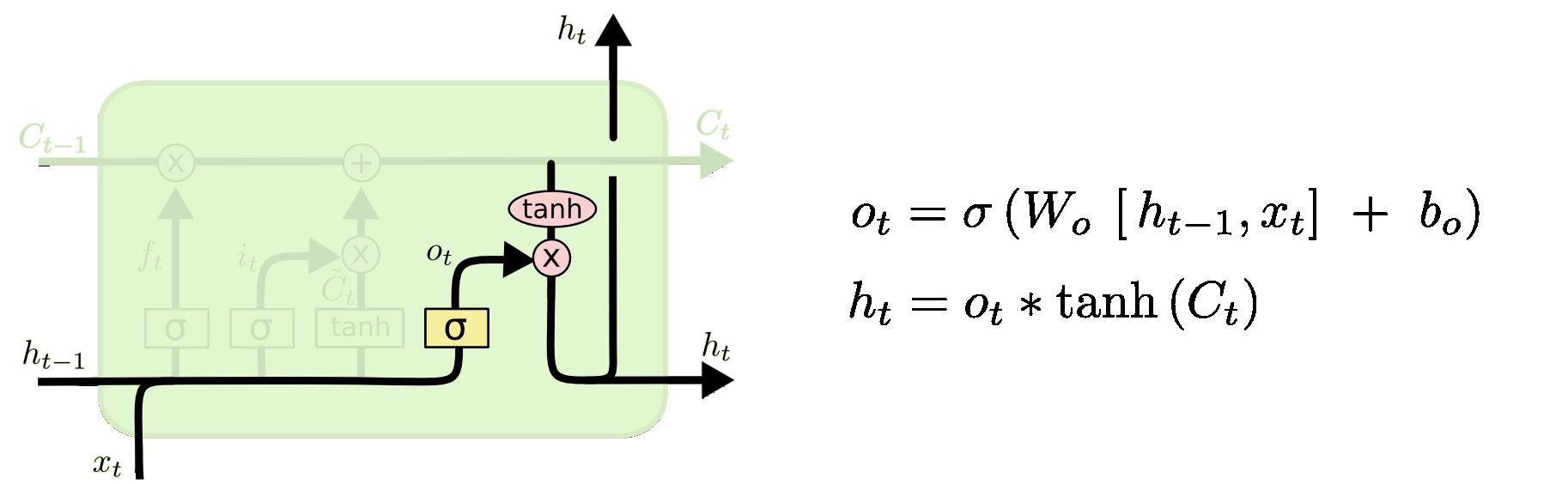
细节注意:
- 新的细胞状态只需要遗忘门和输入门就可以更新,公式为: C t = f t ∗ C t − 1 + i t ∗ C t ~ C_t=f_t*C_t-1+i_t* \\tildeC_t Ct=ft∗Ct−1+it∗Ct~(注意所有的 ∗ * ∗都表示Hadamard 乘积)
- 只有隐状态h_t会传递到输出层,记忆元完全属于内部信息,不可手动修改
三、如何解决RNN中的梯度消失/爆炸问题
解决是指很大程度上缓解,不是让它彻底消失。先解释RNN为什么会有这些问题:
∂
L
t
∂
U
=
∑
k
=
0
t
∂
L
t
∂
O
t
∂
O
t
∂
S
t
(
∏
j
=
k
+
1
t
∂
S
j
∂
S
j
−
1
)
∂
S
k
∂
U
∂
L
t
∂
W
=
∑
k
=
0
t
∂
L
t
∂
O
t
∂
O
t
∂
S
t
(
∏
j
=
k
+
1
t
∂
S
j
∂
S
j
−
1
)
∂
S
k
∂
W
\\beginaligned &\\frac\\partial L_t\\partial U= \\sum_k=0^t\\frac\\partial L_t\\partial O_t\\frac\\partial O_t\\partial S_t(\\prod_j=k+1^t\\frac\\partial S_j\\partial S_j-1)\\frac\\partial S_k\\partial U\\\\&\\frac\\partial L_t\\partial W= \\sum_k=0^t\\frac\\partial L_t\\partial O_t\\frac\\partial O_t\\partial S_t(\\prod_j=k+1^t\\frac\\partial S_j\\partial S_j-1)\\frac\\partial S_k\\partial W \\endaligned
∂U∂Lt=k=0∑t∂Ot∂Lt∂St∂Ot(j=k+1∏t∂Sj−1∂Sj)∂U∂Sk∂W∂Lt=k=0∑t∂Ot∂Lt∂St∂Ot(j=k+1∏t∂Sj−1∂Sj)∂W∂Sk(具体过程可以看这里)
上面是训练过程任意时刻更新W、U需要用到的求偏导的结果。实际使用会加上激活函数,通常为tanh、sigmoid等
tanh和其导数图像如下

sigmoid和其导数如下
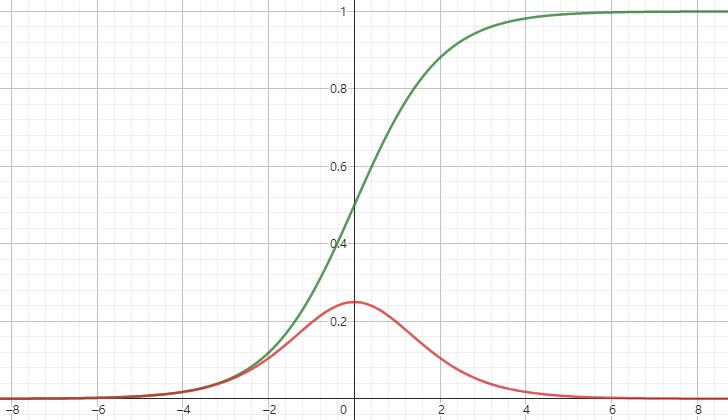
这些激活函数的导数都比1要小,又因为
∏
j
=
k
+
1
t
∂
S
j
∂
S
j
−
1
=
∏
j
=
k
+
1
t
t
a
n
h
′
(
W
s
)
\\prod_j=k+1^t\\frac\\partial S_j\\partial S_j-1=\\prod_j=k+1^ttanh'(W_s)
∏j=k+1t∂Sj−1∂Sj=∏j=k+1ttanh′(Ws),所以当
W
s
W_s
Ws过小过大就会分别造成梯度消失和爆炸的问题,特别是过小。
LSTM如何缓解
由链式法则和三个门的公式可以得到:
∂
C
t
∂
C
t
−
1
=
∂
C
t
∂
f
t
∂
f
t
∂
h
t
−
1
∂
h
t
−
1
∂
C
t
−
1
+
∂
C
t
∂
i
t
∂
i
t
∂
h
t
−
1
∂
h
t
−
1
∂
C
t
−
1
+
∂
C
t
∂
C
t
~
∂
C
t
~
∂
h
t
−
1
∂
h
t
−
1
∂
C
t
−
1
+
∂
C
t
∂
C
t
−
1
=
C
t
−
1
σ
′
(
⋅
)
W
f
∗
o
t
−
1
t
a
n
h
′
(
C
t
−
1
)
+
C
t
~
σ
′
(
⋅
)
W
i
∗
o
t
−
1
t
a
n
h
′
(
C
t
−
1
)
+
i
t
t
a
n
h
′
(
⋅
)
W
c
∗
o
t
−
1
t
a
n
h
′
(
C
t
−
1
)
+
f
t
\\beginaligned &\\frac\\partial C_t\\partial C_t-1\\\\&=\\frac\\partial C_t\\partial f_t\\frac\\partial f_t\\partial h_t-1\\frac\\partial h_t-1\\partial C_t-1+\\frac\\partial C_t\\partial i_t\\frac\\partial i_t\\partial h_t-1\\frac\\partial h_t-1\\partial C_t-1+\\frac\\partial C_t\\partial \\tildeC_t\\frac\\partial \\tildeC_t\\partial h_t-1\\frac\\partial h_t-1\\partial C_t-1+\\frac\\partial C_t\\partial C_t-1\\\\ &=C_t-1\\sigma '(\\cdot)W_f*o_t-1tanh'(C_t-1)+\\tildeC_t\\sigma '(\\cdot)W_i*o_t-1tanh'(C_t-1)\\\\&+i_ttanh'(\\cdot)W_c*o_t-1tanh'(C_t-1)+f_t \\endaligned
r plotly 3d曲面图问题