😆 机器学习采样方法大全

Posted 2021-03-26 samshare

?? Index

• 数据采样的原因
• 常见的采样算法
• 失衡样本的采样
• 采样的Python实现

?? 数据采样的原因

其实我们在训练模型的过程，都会经常进行数据采样，为了就是让我们的模型可以更好的去学习数据的特征，从而让效果更佳。但这是比较浅层的理解，更本质上，数据采样就是对随机现象的模拟，根据给定的概率分布从而模拟一个随机事件。另一说法就是用少量的样本点去近似一个总体分布，并刻画总体分布中的不确定性。

因为我们在现实生活中，大多数数据都是庞大的，所以总体分布可能就包含了无数多的样本点，模型是无法对这些海量的数据进行直接建模的（至少目前而言），而且从效率上也不推荐。

因此，我们一般会从总体样本中抽取出一个子集来近似总体分布，这个子集被称为“训练集”，然后模型训练的目的就是最小化训练集上的损失函数，训练完成后，需要另一个数据集来评估模型，也被称为“测试集”。

采样的一些高级用法，比如对样本进行多次重采样，来估计统计量的偏差与方法，也可以对目标信息保留不变的情况下，不断改变样本的分布来适应模型训练与学习（经典的应用如解决样本不均衡的问题）。

?? 常见的采样算法

采样的原因在上面已经阐述了，现在我们来了解一下采样的一些算法：

01 逆变换采样

有的时候一些分布不好直接采样，可以用函数转换法，如果存在随机变量x和u的变换关系：u=?(x)，则它们的概率密度函数如下所示：

p(u)|?′(x)|=p(x)

因此，如果从目标分布p(x)中不好采样x，可以构造一个变换u=?(x)，使得从变换后地分布p(u)中采样u比较容易，这样可以通过对u进行采样然后通过反函数$$x = phi ^{-1}(u) $$ 来间接得到x。如果是高维空间地随机变量,则?′(x)对应Jacobian行列式。

而且，如果变换关系?(·)是x的累积分布函数的话，则就是我们说的 逆变换采样（Inverse Transform Sampling）， 我们假设待采样的目标分布的概率密度函数为p(x), 它的累积分布函数为：
$$
u = phi(x)=int_{-infty}^x p(t) dt
$$
逆变换采样法的过程：

• 从均匀分布U(0，1)产生一个随机数 $$u_i$$
• 计算逆函数 $$x_i = phi ^{-1}(u_i) $$ 来间接得到x

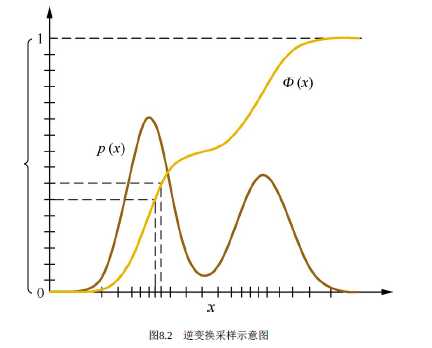
但并不是所有的目标分布的累积分布函数的逆函数都是可以求解的（or容易计算），这个时候逆变换采样法就不太适用，可以考虑拒绝采样（Rejection Sampling）和重要度采样（Importance Sampling）。

02 拒绝采样（Rejection Sampling）

拒绝采样，也被称为接受采样（Accept Sampling），对于目标分布p(x)，选取一个容易采样的参考分布q(x)，使得对于任意的x都有 $$p(x) leq M cdot q(x)$$ ，其采样过程如下：
1）从参考分布q(x)中随机抽取一个样本$$x_i$$
2）从均匀分布U(0,1)产生一个随机数$$u_i$$
3）如果 $$u_i < frac {p(x_i)}{M cdot q(x_i)} $$ , 则接受样本$$x_i$$，否则拒绝，一直重复1-3步骤，直到新产生的样本量满足要求。
其实，拒绝采样的关键就是为我们的目标分布p(x)选取一个合适的包络函数 $$M cdot q(x)$$，如下图所示的正态分布的函数：

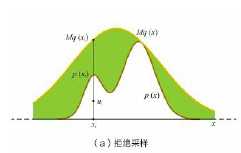
可以知道，包络函数越“紧”，$$p(x_i)$$与$$M cdot q(x_i)$$的大小越接近，那么$$ frac {p(x_i)}{M cdot q(x_i)} $$就越接近1，那么更容易接受采样样本A，这样子采样的效率就越高。

除了上面的形式，还有一种叫自适应拒绝采样（Adaptive Rejection Sampling），在目标分布是对数凹函数时，用分段的线性函数来做包络函数，如下图所示：

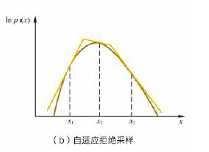
03 重要性采样（Importance Sampling）

还有一种采样方法，是计算函数f(x)在目标分布p(x)上的积分（函数期望），即：
$$
E[f] = int f(x)p(x)dx
$$
我们先找一个比较容易抽样的参考分布q(x)，并令 $$w(x)=frac {P(x)}{q(x)} $$，则存在：
$$
E[f] = int {f(x)w(x)q(x)} dx
$$
这里的w(x)我们可以理解为权重，我们就可以从参考分布q(x)中抽取N个样本$$x_i$$ ，并且利用如下公式来估计$$ E[f]$$ ：
$$
E[f] approx hat{E}N[f] = sum{i=1}^n f(x_i) w(x_i)
$$
下图就是重要性采样的示意图：

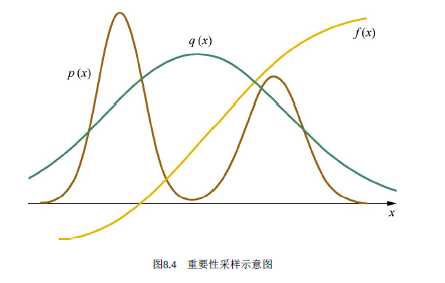
04 马尔科夫蒙特卡洛采样法

在高维空间中，拒绝采样和重要性采样很难寻找到合适参考分布，而且采样的效率是很低的，这个时候是可以考虑一下马尔科夫蒙特卡洛（Markov Chain Monte Carlo，MCMC）采样法。

可能有一些同学对这个名词还是比较陌生，那么先来讲解一下MCMC。

1. 主要思想

MCMC采样法主要包括两个MC，即Monte Carlo和Markov Chain。Monte Carlo是指基于采样的数值型近似求解方法，Markov Chain则是用于采样，MCMC的基本思想是：针对待采样的目标分布，构造一个马尔科夫链，使得该马尔科夫链的平稳分布就是目标分布，然后从任何一个初始状态出发，沿着马尔科夫链进行状态转移，最终得到的状态转移序列会收敛到目标分布，由此得到目标分布的一系列样本。

MCMC有着不同的马尔科夫链（Markov Chain），不同的链对应不用的采样法，常见的两种就是Metropolis-Hastings采样法和吉布斯采样法。

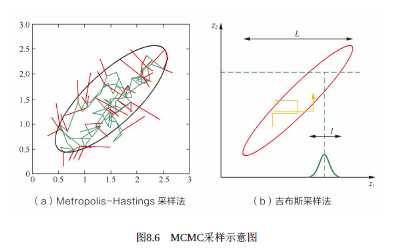
2. Metropolis-Hastings采样法

对于目标分布p(x)，首先选择一个容易采样的参考条件分布 $$q(x^* | x) $$ ，并令
$$
A(x, x^) = min { 1, frac{p(x^)q(x|x^)}{p(x)q(x^|x)} }
$$
然后根据如下过程进行采样：

1）随机选取一个初始样本 $$ x^{(0)} $$

2）For t =1, 2, 3, ...:

{ 根据参考条件分布 $$ q(x^|x^{(t-1)}) $$抽取一个样本 $$x^$$

根据均匀分布U(0,1)产生随机数u

若 $$u < A(x^{(t-1)}, x^) $$，则令 $$x^{(t)}=x^$$，否则令 $$x^{(t)}=x^{(t-1)}$$ }

上面的图是Metropolis-Hastings的示意过程图，其中红线代表被拒绝的移动（维持旧样本），绿线代表被接受的移动（采纳新样本）。

3. 吉布斯采样法

吉布斯采样法是Metropolis-Hastings的一个特例，其核心是每次只对样本的一个维度进行采样和更新，对于目标分布p(x)，其中 $$x=(x_1, x_2, ..., x_d)$$ 是多维向量，按如下的过程进行采样：

1）随机选择初始状态 $$ x^{(0)} = (x^{(0)}_1, x^{(0)}_2,..., x^{(0)}_d)$$

2）for t = 1, 2, 3, ...:

{ 对前一步产生的样本 $$ x^{(t-1)} = (x^{(t-1)}_1, x^{(t-1)}_2,..., x^{(t-1)}_d)$$，依次采样和更新每个维度的值，即依次抽取分量 $$ x^{(t)}_1 p(x_1 | x^{(t-1)}_2, x^{(t-1)}_3,..., x^{(t-1)}_d)$$

形成新的样本 $$ x^{(t)} = (x^{(t)}_1, x^{(t)}_2,..., x^{(t)}_d)$$

}

同样的上述过程得到的样本序列会收敛到目标分布p(x)，另外步骤2中对样本每个维度的抽样和更新操作，不是必须要按照下标顺序进行的，可以是随机进行的。

在拒绝采样中，如果在某一步得到的样本被拒绝，则该步不会产生新样本，需要重新进行采样，如在MCMC中，每一步都是会产生一个样本的，只是有的时候是保留旧样本罢了，而且MCMC是会在不断迭代过程中逐渐收敛到平稳分布的。

失衡样本的采样

我们在实际的建模中总会遇到很多失衡的数据集，比如点击率模型、营销模型、反欺诈模型等等，往往坏样本（or好样本）的占比才千分之几。虽然目前有些机器学习算法会解决失衡问题，比如XGBoost，但是很多时候还是需要我们去根据业务实际情况，对数据进行采样处理，主要还是分两种方式：

过采样（over-sampling）：从占比较少的那一类样本中重复随机抽样，使得最终样本的目标类别不太失衡；

欠采样（under-sampling）：从占比较多的那一类样本中随机抽取部分样本，使得最终样本的目标类别不太失衡；

科学家们根据上述两类，衍生出了很多方法，如下：

Over-Sampling类

1）Random Oversampling

也就是随机过采样，我们现在很少用它了，因为它是从样本少的类别中随机抽样，再将抽样得来的样本添加到数据集中，从而达到类别平衡的目的，这样子做很多时候会出现过拟合情况。

2）SMOTE

SMOTE，全称是Synthetic Minority Oversampling Technique，其思想就是在少数类的样本之间，进行插值操作来产生额外的样本。对于一个少数类样本$mathbf{x}i$，使用K-Mean法（K值需要人工确定）求出距离$mathbf{x}i$ 距离最近的k个少数类样本，其中距离定义为样本之间n维特征空间的欧式距离，然后从k个样本点钟随机抽取一个，使用下面的公式生成新的样本点：
$$
mathbf{x}{new}=mathbf{x}{i}+(mathbf{hat{x}}{i}-mathbf{x}{i}) imes delta
$$
其中，$mathbf{hat{x}}$ 为选出的k近邻点，$deltain[0,1]$是一个随机数。下图就是一个SMOTE生成样本的例子，使用的是3-近邻，可以看出SMOTE生成的样本一般就在 $mathbf{x}{i}$和$?mathbf{hat{x}}{i}$相连的直线上：

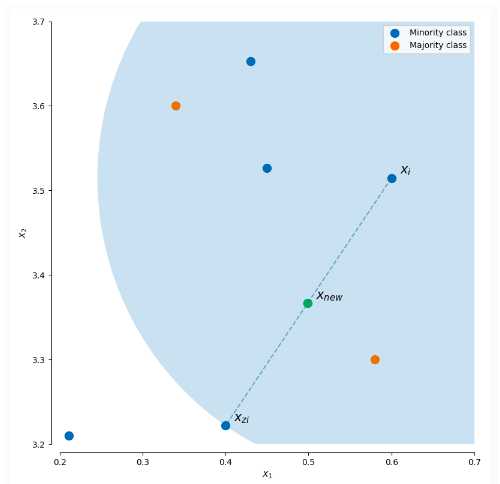
从图中可以看出 $${x}_{new}$$ 就是我们新生成样本点，但是，SMOTE算法也是有缺点的：

（1）如果选取的少数类样本周围都是少数类样本，那么新合成的样本可能不会提供太多有用的信息；

（2）如果选取的少数类样本周围都是多数类样本，那么这可能会是噪声，也无法提升分类效果。

其实，最好的新样本最好是在两个类别的边界附近，这样子最有利于分类，所以下面介绍一个新算法——Border-Line SMOTE。

3）Border-Line SMOTE

这个算法一开始会先将少数类样本分成3类，分别DANGER、SAFE、NOISE，如下图：

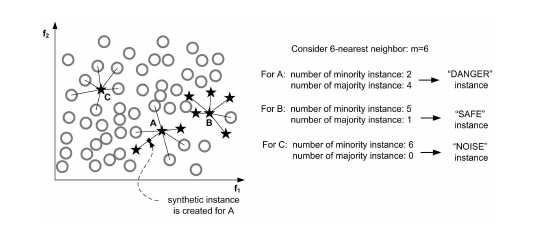
而Border-line SMOTE算法只会在“DANGER”状态的少数类样本中去随机选择，然后利用SMOTE算法产生新样本。

4）ADASYN

ADASYN名为自适应合成抽样(Adaptive Synthetic Sampling)，其最大的特点是采用某种机制自动决定每个少数类样本需要产生多少合成样本，而不是像SMOTE那样对每个少数类样本合成同数量的样本。ADASYN的缺点是易受离群点的影响，如果一个少数类样本的K近邻都是多数类样本，则其权重会变得相当大，进而会在其周围生成较多的样本。

Under-Sampling类

1）Random Undersampling

这类也是比较简单的，就是随机从多数类中删除一些样本，这样子的缺失也是很明显，那就是造成部分信息丢失，整体模型分类效果不理想。

2）EasyEnsemble 和 BalanceCascade

这两个算法放在一起的原因是因为都用到了集成思想来处理随机欠采样的信息丢失问题。

• EasyEnsemble ：将多数类样本随机划分成n份，每份的数据等于少数类样本的数量，然后对这n份数据分别训练模型，最后集成模型结果。
• BalanceCascade：这类算法采用了有监督结合boosting的方式，在每一轮中，也是从多数类中抽取子集与少数类结合起来训练模型，然后下一轮中丢弃此轮被正确分类的样本，使得后续的基学习器能够更加关注那些被分类错误的样本。

3）NearMiss

NearMiss本质上是一种原型选择(prototype selection)方法，即从多数类样本中选取最具代表性的样本用于训练，主要是为了缓解随机欠采样中的信息丢失问题。NearMiss采用一些启发式的规则来选择样本，根据规则的不同可分为3类：

• NearMiss-1：选择到最近的K个少数类样本平均距离最近的多数类样本
• NearMiss-2：选择到最远的K个少数类样本平均距离最近的多数类样本
• NearMiss-3：对于每个少数类样本选择K个最近的多数类样本，目的是保证每个少数类样本都被多数类样本包围

NearMiss-1和NearMiss-2的计算开销很大，因为需要计算每个多类别样本的K近邻点。另外，NearMiss-1易受离群点的影响，如下面第二幅图中合理的情况是处于边界附近的多数类样本会被选中，然而由于右下方一些少数类离群点的存在，其附近的多数类样本就被选择了。相比之下NearMiss-2和NearMiss-3不易产生这方面的问题。

?? Reference

《百面机器学习》—— Chapter 7

机器学习之类别不平衡问题 (3) —— 采样方法

https://nbviewer.jupyter.org/github/massquantity/Class-Imbalance/blob/master/Code_Sampling.ipynb