机器学习集成学习(未完成)
Posted 4privetdrive
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习集成学习(未完成)相关的知识,希望对你有一定的参考价值。
集成学习
原理
集成学习是将许多个弱学习器通过策略组合到一起的算法,弱学习器可以是树或是神经网络或者是其他。目前集成学习的方法分为两大类:bagging方法和boosting方法。
bagging与随机森林
bagging方法是从原始数据集中进行多次随机采样,每次采样多个样本。记为T个采样集,每个采样集中包含m个样本。bagging方法既可以用来多分类也可以用来回归:基于T个训练集训练出T个基学习器,对预测输出进行结合时,分类任务使用简单投票法,回归任务使用简单平均法。由于对数据集进行的有放回的抽样,所以最终使用到的数据只占用原始数据的63.2%,剩下的36.8%的数据可以拿来用作验证集,或者对决策树进行剪枝和对神经网络进行提前停止预防过拟合。bagging是低偏差高方差,训练时在降低方差。bagging中的个体学习器不存在强依赖关系,可同时并行化生成。
随机森林方法在bagging分割数据集的基础上更进一步,它使用决策树作为基学习器,决策树的划分的属性集合也是从全部属性集合中采样得到的。即:对于当前节点的属性集合中(假设有d个属性)选择一个包含k个属性的子集,然后再从这个子集中选择一个最优的属性用于划分。推荐值$k=log_{2}d$.
boosting与AdaBoost
boosting方法是先用初始数据集训练一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得前面的基学习器做错的训练样本得到更多的关注,即分错的样本权重增强,下一个基学习器就能着重学习上一个学习器分错的样本数据,如此重复进行,直到基学习器数目达到事先指定的值T或误分率e小于指定值,最终将这T个基学习器进行加权结合。boosting是低方差高偏差的,训练过程在降低偏差。boosting中的个体学习器存在强依赖关系,必须串行序列化生成。
AdaBoost只能用于二分类,其损失函数为指数损失函数算法的步骤如下:
1)给每个训练样本($x_{1},x_{2},….,x_{N}$)分配权重,初始权重$w_{1}$均为1/N。
2)针对带有权值的样本进行训练,得到模型$G_m$(初始模型为G1)。
3)计算模型$G_m$的误分率$e_m=sum_{i=1}^Nw_iI(y_i ot= G_m(x_i))$(直观说法就是分错的占整个数据中的比例)
4)计算模型$G_m$的系数$alpha_m=0.5log[(1-e_m)/e_m]$
5)根据误分率$e$和当前权重向量$w_m$更新权重向量$w_{m+1}$,$Z_{m}$是规范化因子。从下式看到,预测值与真实值一样的数据,权重降低;分错的数据权重升高。
$$w_{m+1,i}=frac{w_{mi}}{Z_{m}}exp(-alpha_{m}y_{i}G_{m}(x_{i}))$$
$$Z_{m}=sum_{i=1}^{N}w_{mi}exp(-alpha_{m}y_{i}G_{m}(x_{i}))$$
6)计算组合模型$f(x)=sum_{m=1}^Malpha_mG_m(x_i)$的误分率。
7)当组合模型的误分率或迭代次数低于一定阈值,停止迭代;否则,回到步骤2)
GBDT
当基学习器变为决策树的时候(一般为CART回归树),boosting方法变成了提升树方法,GBDT的树都是回归树,但它既可以解决回归问题(线性和非线性),也可以解决分类问题(二分类)。
回归树优化以下问题:
$$min_{s}left[ mathop{min}_{c_{1}}sum_{x_{i} in R_{1}}(y_{i}-c_{1})^{2}+mathop{min}_{c_{2}}sum_{x_{i} in R_{2}}(y_{i}-c_{2})^{2} ight]$$
回归问题提升树使用以下前项分步算法:
$$f_{0}(x)=0$$
$$f_{m}(x)=f_{m-1}(x)+T(x; heta_{m}),m=1,2,...,M$$
$$f_{M}(x)=sum_{m=1}^{M}T(x; heta_{m})$$
在使用平方误差损失函数时,有:
$$L(y,f_{m}(x))=(y-f_{m}(x))^{2}=[y-f_{m-1}(x)-T(x; heta_{m})]^{2}=[r-T(x; heta_{m})]^{2}$$
这里
$$r=y-f_{m-1}(x)$$
是当前模型拟合数据的残差,所以对回归问题的提升树算法来说,只需要简单的模拟当前模型的残差。GBDT全名为梯度提升决策树,核心就是利用损失函数的负梯度作为残差的近似值,拟合一个回归树。GBDT损失函数是平方损失时,负梯度就是我们说的残差,此时残差方向就是我们的全局最优方向。损失函数不为平方损失时,用负梯度方向代替残差方向,叫做伪残差。伪残差的方向就是我们的局部最优方向。
在解决分类问题时,需要改变误差函数,由于样本输出不是连续值,而是离散类别,导致我们无法直接从输出类别去拟合类别输出误差。为了解决这个问题,主要有两种方法。一是用指数损失函数,此时GBDT算法退化为AdaBoost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。就是说,我们用的是类别的预测概率值和真实概率值的差来拟合损失。
在GBDT中,每一棵树先乘上一个权重然后再累加,这种技巧叫做Shrinkage,即它不完全信任每一个棵残差树,它认为每棵树只学到了真理的一小部分,累加的时候只累加一小部分。
XGBoost
XGBoost在决策树的构建阶段加入了正则项:
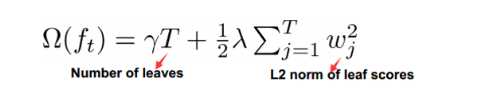
同时,XGBoost的损失函数在现有的t-1棵树最优解处泰勒展开,可加快推导速度
代码实现
面试问题
GBDT算法的优缺点。
优点:
- 预测精度高
- 计算速度快
- 泛化能力、表达能力好
- 适合低维数据
- 能处理非线性数据
- 具有较好的解释性与鲁棒性,能够自动发现特征间的高阶关系,并且也不需要对数据进行特殊的预处理与归一化等
缺点:
- 并行麻烦(因为上下两棵树有联系)
- 如果数据维度较高时会加大算法的计算复杂度,高维时不如SVM或者神经网络
- GBDT在处理文本分类特征问题上,相对于其他模型的优势不如它在处理数值特征时明显
参考文献
西瓜书
统计学习基础
https://blog.csdn.net/fjsd155/article/details/93537416
以上是关于机器学习集成学习(未完成)的主要内容,如果未能解决你的问题,请参考以下文章