各种排序的稳定性，时间复杂度空间复杂度稳定性

Posted 2021-03-24 haizai

各种排序的稳定性，时间复杂度、空间复杂度、稳定性总结如下图：

 

 

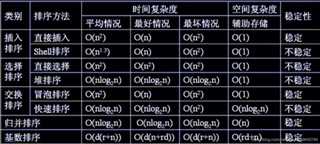
关于时间复杂度：
    (1)平方阶(O(n2))排序
    各类简单排序:直接插入、直接选择和冒泡排序；
    (2)线性对数阶(O(nlog2n))排序
    　　快速排序、堆排序和归并排序；
    (3)O(n1+§))排序,§是介于0和1之间的常数。
    希尔排序
    (4)线性阶(O(n))排序
    基数排序，此外还有桶、箱排序。

    关于稳定性：
    稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序
    不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序    
        
    #include<iostream>
         2 #include<malloc.h>
         3 using namespace std;
         4 
         5 int getdigit(int x,int d)  
         6 {   
         7     int a[] = {1, 1, 10};     //因为待排数据最大数据也只是两位数，所以在此只需要到十位就满足
         8     return ((x / a[d]) % 10);    //确定桶号
         9 }  
        10 
        11 void  PrintArr(int ar[],int n)
        12 {
        13     for(int i = 0; i < n; ++i)
        14         cout<<ar[i]<<" ";
        15     cout<<endl;
        16 }
        17 
        18 void msdradix_sort(int arr[],int begin,int end,int d)  
        19 {     
        20     const int radix = 10;   
        21     int count[radix], i, j; 
        22     //置空
        23     for(i = 0; i < radix; ++i)   
        24     {
        25         count[i] = 0;   
        26     }
        27     //分配桶存储空间
        28     int *bucket = (int *) malloc((end-begin+1) * sizeof(int));    
        29     //统计各桶需要装的元素的个数  
        30     for(i = begin;i <= end; ++i)   
        31     {
        32         count[getdigit(arr[i], d)]++;   
        33     }
        34     //求出桶的边界索引，count[i]值为第i个桶的右边界索引+1
        35     for(i = 1; i < radix; ++i)   
        36     {
        37         count[i] = count[i] + count[i-1];    
        38     }
        39     //这里要从右向左扫描，保证排序稳定性 
        40     for(i = end;i >= begin; --i)          
        41     {    
        42         j = getdigit(arr[i], d);      //求出关键码的第d位的数字， 例如：576的第3位是5   
        43         bucket[count[j]-1] = arr[i];   //放入对应的桶中，count[j]-1是第j个桶的右边界索引   
        44         --count[j];                    //第j个桶放下一个元素的位置(右边界索引+1)   
        45     }   
        46     //注意：此时count[i]为第i个桶左边界    
        47     //从各个桶中收集数据  
        48     for(i = begin, j = 0;i <= end; ++i, ++j)  
        49     {
        50         arr[i] = bucket[j]; 
        51     }       
        52     //释放存储空间
        53     free(bucket);   
        54     //对各桶中数据进行再排序
        55     for(i = 0;i < radix; i++)  
        56     {   
        57         int p1 = begin + count[i];         //第i个桶的左边界   
        58         int p2 = begin + count[i+1]-1;     //第i个桶的右边界   
        59         if(p1 < p2 && d > 1)  
        60         {
        61             msdradix_sort(arr, p1, p2, d-1);  //对第i个桶递归调用，进行基数排序，数位降 1    
        62         }
        63     }  
        64 } 
        65 
        66 void  main()
        67 {
        68     int  ar[] = {12, 14, 54, 5, 6, 3, 9, 8, 47, 89};
        69     int len = sizeof(ar)/sizeof(int);
        70     cout<<"排序前数据如下："<<endl;
        71     PrintArr(ar, len);
        72     msdradix_sort(ar, 0, len-1, 2);
        73     cout<<"排序后结果如下："<<endl;
        74     PrintArr(ar, len);
        75 } 
        76 
        77 排序前数据如下：
        78 12 14 54 5 6 3 9 8 47 89
        79 排序后结果如下：
        80 3 5 6 8 9 12 14 47 54 89
        81  
        
        
第二种方式排序基数 : 
        #include<iostream>
         2 #include<malloc.h>
         3 using namespace std;
         4 
         5 #define   MAXSIZE   10000
         6 
         7 int getdigit(int x,int d)  
         8 {   
         9     int a[] = {1, 1, 10, 100};   //最大三位数，所以这里只要百位就满足了。
        10     return (x/a[d]) % 10;  
        11 }  
        12 void  PrintArr(int ar[],int n)
        13 {
        14     for(int i = 0;i < n; ++i)
        15     {
        16         cout<<ar[i]<<" ";
        17     }
        18     cout<<endl;
        19 }  
        20 void lsdradix_sort(int arr[],int begin,int end,int d)  
        21 {    
        22     const int radix = 10;   
        23     int count[radix], i, j; 
        24 
        25     int *bucket = (int*)malloc((end-begin+1)*sizeof(int));  //所有桶的空间开辟   
        26    
        27     //按照分配标准依次进行排序过程
        28     for(int k = 1; k <= d; ++k)  
        29     {  
        30         //置空
        31         for(i = 0; i < radix; i++)  
        32         {
        33             count[i] = 0;        
        34         }               
        35         //统计各个桶中所盛数据个数
        36         for(i = begin; i <= end; i++) 
        37         {
        38            count[getdigit(arr[i], k)]++;
        39         }
        40         //count[i]表示第i个桶的右边界索引
        41         for(i = 1; i < radix; i++) 
        42         {
        43             count[i] = count[i] + count[i-1];
        44         }
        45         //把数据依次装入桶(注意装入时候的分配技巧)
        46         for(i = end;i >= begin; --i)        //这里要从右向左扫描，保证排序稳定性   
        47         {    
        48             j = getdigit(arr[i], k);        //求出关键码的第k位的数字， 例如：576的第3位是5   
        49             bucket[count[j]-1] = arr[i]; //放入对应的桶中，count[j]-1是第j个桶的右边界索引 
        50             --count[j];               //对应桶的装入数据索引减一  
        51         } 
        52 
        53         //注意：此时count[i]为第i个桶左边界  
        54         
        55         //从各个桶中收集数据
        56         for(i = begin,j = 0; i <= end; ++i, ++j)  
        57         {
        58             arr[i] = bucket[j];    
        59         }        
        60     }     
        61     free(bucket);   
        62 }  
        63 
        64 void  main()
        65 {
        66     int  br[10] = {20, 80, 90, 589, 998, 965, 852, 123, 456, 789};
        67     cout<<"原数据如下："<<endl;
        68     PrintArr(br,10);
        69     lsdradix_sort(br, 0, 9, 3);
        70     cout<<"排序后数据如下："<<endl;
        71     PrintArr(br, 10);
        72 }
        73 /*
        74 原数据如下：
        75 20 80 90 589 998 965 852 123 456 789
        76 排序后数据如下：
        77 20 80 90 123 456 589 789 852 965 998
        78