特殊矩阵的压缩存储

Posted 2021-03-13 zws-bugging

所谓特殊矩阵：是指矩阵中值相同的元素或者零元素的分布有一定的规律。常见的特殊矩阵有：对称矩阵、三角矩阵、对角矩阵。注意：它们都是方阵，即行数和列数相同。

主对角线：在矩阵中每个元素的行标等于纵标（i==j）。

上三角：在矩阵中每个元素的行标小于纵标（i<j）。

下三角：在矩阵中每个元素的行标大于纵标（i>j）。

一、对称矩阵的压缩存储

一个n阶方阵A[n][n]中的元素满足ai,j=aj,i(0<=i,j<=n-1),则称其为n阶对称矩阵。

压缩存储：由于元素关于主对角线对称，在存储时只存储对称矩阵的上三角或下三角元素，使得对称的元素共享一个存储空间。（以行序为主序存储其下三角+主对角线的元素，一共要存储n*(n+1)/2个元素）

 

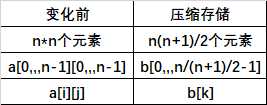
 由于k的序号=所有它前面元素的个数=所在行前面行的所有元素+所在行它前面的元素（包括本身）。

一维数组k与与二维数组元素的i、j之间的关系：

当i>=j时，k=i*(i+1)/2 + j;//本例都是以0为开始的下标，以下也是类同。

当i<j时，k=j*(j+1)/2+i;

二、三角矩阵的压缩矩阵

上三角矩阵：当一个方阵的主角线以下的所有元素皆为零；

当i<=j时，k=(i-1)*(2n-i+2)/2+j-2;(以下公式为了方便理解，i,j,k都是从1开始)

矩阵元素压缩放在一维数组上，可以理解为：

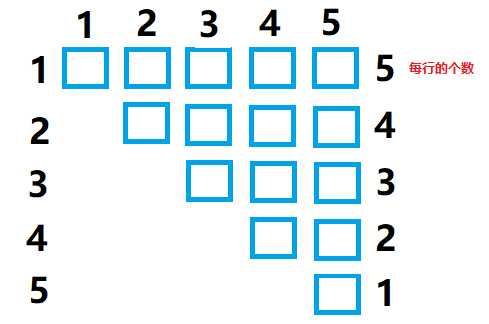
如5*5矩阵上三角矩阵第一行为5个元素，第二行为4个元素...最后一行为1个元素（也就是元素个数逐减的等差数列an=n-i+1，an代表每行的个数，i代表的是第几项（第几行），所以a1=n-1+1=n,当前行的前面所有行的元素和：s(i-1)=n(a1+an)/2=(i-1)*[n+(n-（i-1)+1)]=(i-1)*(2n-i+2)/2）

如：a[3][3]=b[10],s2=5+4=9，所以k=s2+j-2=10。

 

下三角矩阵：当一个方阵的主角线以上的所有元素皆为零；

当i>=j时，k=i*(i+1)/2+j-2;