ZJNU 2136 - 会长的正方形

Posted 2021-03-13 stelayuri

对于n*m网格

取min(n,m)作为最大的正方形边长

则答案可以表示成

s=1~min(n,m)

对于一个s*s的正方形

 

用oblq数组储存有多少四个角都在这个正方形边上的正方形

以4*4为例

除了4*4自身外，四个角在边上的正方形还有

 

 

 

 

 

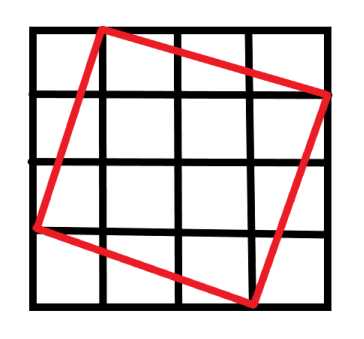
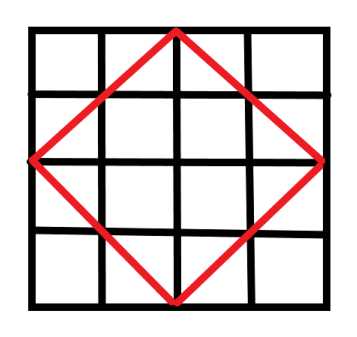
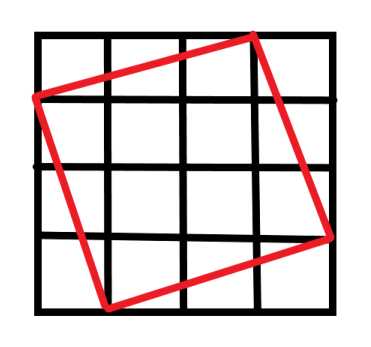
所以4*4网格最多可以有4种正方形存在

推出s*s网格最多可以有s种正方形存在

单看这些正方形在网格上侧的点所在位置

可以发现这种“斜正方形”共有s-1种情况

且每个正方形的边长为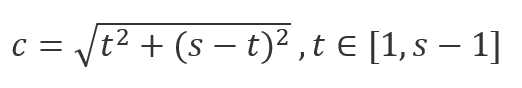

 

因为S=c^2

所以每个正方形面积为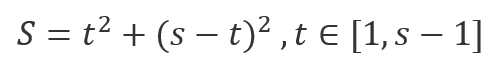

 

取和，加上原本的面积s*s，存放在oblq[s]内便于引用

 

然后考虑组合情况

对于一个n*m的网格，里面可以组合出(n-s+1)*(m-s+1)种s*s的正方形

所以每次数量加上(n-s+1)*(m-s+1)*s

面积加上(n-s+1)*(m-s+1)*oblq[s]

取和即可得到答案

 

代码多加了个t变量，每次让n和m递减，t递增，意义不变

 1 /*
 2 Written By. StelaYuri
 3 On 2020/01/15
 4 */
 5 #include<bits/stdc++.h>
 6 using namespace std;
 7 typedef long long ll;
 8 const ll mod=1000000007;
 9 ll oblq[10005];
10 int main(){
11     ios::sync_with_stdio(0);
12     cin.tie(0);cout.tie(0);
13     ll T,n,m,i,j,t,N,S;
14     for(i=1;i<=10000;i++){
15         oblq[i]=i*i;
16         for(j=1;j<i;j++)
17             oblq[i]+=j*j+(i-j)*(i-j);
18         oblq[i]%=mod;
19     }
20     cin>>T;
21     while(T--){
22         cin>>n>>m;
23         N=S=0;
24         t=1;
25         while(n&&m){
26             N=(N+n*m*t)%mod;
27             S=(S+n*m*oblq[t])%mod;
28             n--;
29             m--;
30             t++;
31         }
32         cout<<N<<‘ ‘<<S<<endl;
33     }
34     
35     return 0;
36 }