第五关——数论:组合数学
Posted wybxz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第五关——数论:组合数学相关的知识,希望对你有一定的参考价值。
20:44:00 你在台上唱着我的创作,布局谋篇像本悲情小说——许嵩《最佳歌手》
我的寒假,我美好的寒假啊啊啊
“其实我还蛮不想写你的,博客,可是没办法啊,谁叫我的寒假不要我了,我就只好要你了,博客”
目录
-
鸽巢原理
-
鸽巢原理推广
-
杨辉三角和二项式系数
-
容斥定理
-
卡特兰数
-
斯特林数
那接下来就要来看一下鸽巢原理(抽屉原理)啦
也不知道发现它的人是不是看着别人鸽子的窝盯半天才发现的,人家鸽子会不好意思的啦!
-
定义:如果有n+1个鸽子要进n个鸽巢,则至少存在一个鸽巢种包含两个或更多的鸽子。
-
例题:
(2010问题求解3)记T为一队列,初始时为空,现有n个总和不超过32的正整数依次入队。如果无论这些数具体为何值,都能找到一种出队的方式,使得存在某个时刻队列T中的数之和恰好为9,那么n的最小值是_________。
由题意可知bi取值范围为1-32,现将这32个数构造为集合{1,10},{2,11}, …, {8,17}, {18,27}, {19,28},…,{23,32} ,{24},{25},{26},这17个集合中的任一个集合不能包含两个或两个以上的 ,否则它们的差为9,故由鸽巢定理可得出,n的最小值为18. -
应用:
在边长为1的正方形内任取5点,则其中至少有2点的距离不超过√2/2
-
例题:
这道题是典型的鸽巢原理,可用鸽巢原理一种简单的推理方法隔板法进行分析,如果S<N-1.把S个糖果放到隔板之间,这N个隔板不够放.必然至少有两个隔板之间没有糖果,由于这两个隔板是同一种糖果,所以无解。反之则有解。
注意开long long(尽管数据不大)
#include <cstdio> #include<math.h> #include<algorithm> using namespace std; int main() { int i,j,n,sum,max_,t; scanf("%d",&t); { while(t--) { sum=max_=0; scanf("%d",&n); int *a=(int*)malloc(sizeof(int)*n); for(i=0;i<n;i++) { scanf("%d",&a[i]); max_=max(max_,a[i]); } for(i=0;i<n;i++) { if(a[i]!=max_) sum+=a[i]; if(sum>=max_-1) break; } if(i==n) printf("No "); else printf("Yes "); } } }
鸽巢原理推广
-
鸽巢原理的加强形式
定理: 令q1, q2, q3, ...., qn为正整数。如果将 q1, q2, q3, ...., qn - n + 1 个物体放到n个盒子中,则存在一个i,使得第i个盒子至少含有qi个物品 ;
证明: 假设将q1, q2, q3, ...., qn - n + 1个物品分别放到n个盒子里。如果每一个i (i = {1, 2, ..n}),第i个盒子中放少于qi 个物品,则所有盒子所放物品的总数不超过
(q1 - 1) + (q2 - 1) + ... + (qn - 1) = q1 + q2 + ... + qn - n
显然,比所要放的总数少一个。因此可以确定,对某个i (i = {1, 2, .. n}),第i个盒子至少包含qi个物品。
-
Erdös-Szekeres定理
简单来说呢,就是在由n2+1n2+1个实数构成的序列中,必然含有长为n+1n+1的单调(增或减)子序列。
-
Ramsey定理
-
定义:对于一个给定的两个整m,n>=2,则一定存在一个最小整数r,使得用两种颜色(例如红蓝)无论给Kr的每条边如何染色,总能找到一个红色的Km或者蓝色的Kn。显然,当p>=r的时候,Kp也满足这个性质。
-
表示形式:r可以看做一个有关m,n的二元函数,即r(m,n)。r(3,3)=6.
-
性质:
①等价性 r(m,n)=r(n,m)
②r(2,n)=n k2较特殊 只有一条边 最小的kr为Kn
③r(m,2)=m
-
数表:
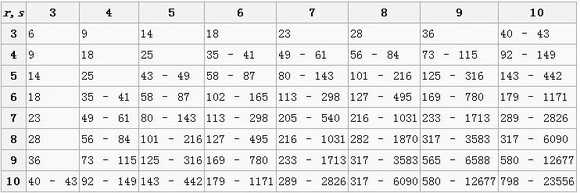
例题
问题很显然,6以及6以上的直接统计345的暴力统计就行了
就是说ans=3的个数+4的个数+5的个数+C(n,6)C(n,7)+…………+C(n,n)=2^n-C(n,0)-C(n,1)-C(n,2)-3不合法的个数-4不合法的个数-5不合法的个数。
#include<bits/stdc++.h> using namespace std; const int maxn=55; const int mod=1000000007; int T; int a[maxn][maxn]; int cc=1; int m,n; void input(){ scanf("%d%d",&n,&m); for (int i=1;i<=m;i++){ int u,v; scanf("%d%d",&u,&v); a[u][v]=a[v][u]=1; } } bool ch(int x,int y,int z){ int t=a[x][y]+a[x][z]+a[y][z]; if (t==0||t==3)return true; return false; } bool h(int x,int y,int z,int w){ return (ch(x,y,z)||ch(x,y,w)||ch(x,z,w)||ch(y,z,w)); } bool e(int a,int b,int c,int d,int e){ return (ch(a,b,c)||ch(a,b,d)||ch(a,b,e)||ch(a,c,d)||ch(a,c,e)||ch(a,d,e)||ch(b,c,d)||ch(b,c,e)||ch(b,d,e)||ch(c,d,e)); } void solve(){ long long ans=1; for (int i=1;i<=n;i++){ ans = ans*2; ans%=mod; } ans-=n,ans--; ans-=n*(n-1)/2; ans+=mod; ans%=mod; for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) for(int k=j+1;k<=n;k++) if(!ch(i,j,k))ans--; for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) for(int k=j+1;k<=n;k++) for(int l=k+1;l<=n;l++) if(!h(i,j,k,l))ans--; for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) for(int k=j+1;k<=n;k++) for(int l=k+1;l<=n;l++) for(int p=1+l;p<=n;p++) if(!e(i,j,k,l,p))ans--; ans+=mod; ans%=mod; printf("Case #%d: %lld ",cc++,ans); } int main(){ scanf("%d",&T); while (T--){ memset(a,0,sizeof(a)); scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ int u,v; scanf("%d%d",&u,&v); a[u][v]=a[v][u]=1; } solve(); } return 0; }
这道题就是鸽巢原理的运用。
#include<bits/stdc++.h> using namespace std; const int maxn=1e5+10; const int mod=1e9+7; typedef long long ll; ll vis[maxn], a[maxn]; int main() { std::ios::sync_with_stdio(false); ll n, m; while(cin>>n>>m){ if(!n&&!m){ break; } ll sum=0,t; memset(vis,0,sizeof(vis) ); for(ll i=1;i<=m;i++) cin>>a[i]; for(ll i=1;i<=m;i++) { sum+=a[i]; t=sum%n; if(t==0) { for(ll j=1;j<i;j++) cout<<j<<" "; cout<<i<<endl; break; } else if(vis[t]) { for(ll j=vis[t]+1;j<i;j++) cout<<j<<" "; cout << i << endl; break; } vis[t] = i; } } return 0; }
这道题用到的是Ramsey定理
#include<bits/stdc++.h> using namespace std; int T,n; int main() { scanf("%d",&T); while(T--) { scanf("%d",&n); int a[10][10]={0}; for(int i=1; i<n; ++i) for(int j=i+1; j<=n; ++j) { int t; scanf("%d",&t); if(t&&n<6) a[i][j]=a[j][i]=1; } if(n>=6) { puts("Bad Team!"); continue; } int f=0; for(int i=1;i<=n;++i) for(int j=i+1;j<=n;++j) for(int k=j+1;k<=n;++k) if(a[i][j]&&a[i][k]&&a[j][k]) { f=1; break; } if(f) puts("Bad Team!"); else puts("Great Team!"); } return 0; }
22:19:37 如果这失忆变成了洪水,也对,也对。——鬼卞《失眠症》
杨辉三角和二项式系数
杨辉三角小的时候都学过,那么杨辉三角有些什么规律呢,大家也都知道,那么求杨辉三角除了递推打表还有下面这种方法:以上是关于第五关——数论:组合数学的主要内容,如果未能解决你的问题,请参考以下文章
hdu 6088 Rikka with Rock-paper-scissors (2017 多校第五场 1004) 组合数学 + 数论 + 模意义下的FFT