感知机算法及BP神经网络

Posted 2020-11-15 twzh123456

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了感知机算法及BP神经网络相关的知识，希望对你有一定的参考价值。

简介：感知机在1957年就已经提出，可以说是最为古老的分类方法之一了。是很多算法的鼻祖，比如说BP神经网络。虽然在今天看来它的分类模型在很多数时候泛化能力不强，但是它的原理却值得好好研究。先学好感知机算法，对以后学习神经网络，深度学习等会有很大的帮助。

一，感知机模型

（1）、超平面的定义

令w₁，w₂，...w_n，v都是实数(R) ，其中至少有一个w_i不为零，由所有满足线性方程w₁*x₁+w₂*x₂+...+w_n*x_n=v

的点X=[x₁,x₂,...x_n]组成的集合，称为空间R的超平面。

从定义可以看出：超平面就是点的集合。集合中的某一点X，与向量w=[w₁，w₂，...w_n]的内积，等于v

特殊地，如果令v等于0，对于训练集中某个点X：

w*X=w₁*x₁+w₂*x₂+...+w_n*x_n>0，将X标记为一类

w*X=w₁*x₁+w₂*x₂+...+w_n*x_n<0，将X标记为另一类

（2）、数据集的线性可分

对于数据集T={(X₁, y₁),(X₂, y₂)...(X_N, y_N)}，X_i belongs to Rⁿ，y_i belongs to {-1, 1}，i=1,2,...N

若存在某个超平面S：w*X=0

将数据集中的所有样本点正确的分类，则称数据集T线性可分。

所谓正确地分类，就是：如果w*X_i>0，那么样本点(X_i, y_i)中的 y_i 等于1

如果w*X_i<0，那么样本点(X_i, y_i)中的 y_i 等于-1

因此，给定超平面 w*X=0，对于数据集 T中任何一个点(X_i, y_i)，都有y_i(w*X_i)>0，这样T中所有的样本点都被正确地分类了。

如果有某个点(X_i, y_i)，使得y_i(w*X_i)<0，则称超平面w*X对该点分类失败，这个点就是一个误分类的点。

（3）、感知机模型

f(X)=sign(w*X+b)，其中sign是符号函数。

感知机模型，对应着一个超平面w*X+b=0，这个超平面的参数是(w,b)，w是超平面的法向量，b是超平面的截距。

我们的目标是，找到一个(w,b)，能够将线性可分的数据集T中的所有的样本点正确地分成两类。

二、感知机策略

策略的重点是定义损失函数，即构造出一种能都使得损失最小的函数结构

三、感知机算法

算法的输入为m个样本，每个样本对应于n维特征和一个二元类别输出1或者-1，如下：　　(x(0)1,x(0)2,...x(0)n,y0),(x(1)1,x(1)2,...x(1)n,y1),...(x(m)1,x(m)2,...x(m)n,ym)(x1(0),x2(0),...xn(0),y0),(x1(1),x2(1),...xn(1),y1),...(x1(m),x2(m),...xn(m),ym)

　　　　输出为分离超平面的模型系数θ向量

　　　　算法的执行步骤如下：

　　　　（1）定义所有x0x0为1。选择θ向量的初值和步长α的初值。可以将θ向量置为0向量，步长设置为1。要注意的是，由于感知机的解不唯一，使用的这两个初值会影响θ向量的最终迭代结果。

　　　　（2）在训练集里面选择一个误分类的点(x(i)1,x(i)2,...x(i)n,yi)(x1(i),x2(i),...xn(i),yi), 用向量表示即(x(i),y(i))(x(i),y(i))，这个点应该满足：y(i)θ?x(i)≤0y(i)θ?x(i)≤0

　　　　（3）对θ向量进行一次随机梯度下降的迭代：θ=θ+αy(i)x(i)θ=θ+αy(i)x(i)

　　　　（4）检查训练集里是否还有误分类的点，如果没有，算法结束，此时的θ向量即为最终结果。如果有，继续第2步。

四、感知机与感知机神经网络代码实现

net=newp([0 2],1);
inputweights=net.inputweights{1,1};
biases=net.biases{1};

net=newp([-2 2;-2 2],1);
net.IW{1,1}=[-1 1];
net.IW{1,1}
net.b{1}=1;
net.b{1}
p1=[1;1],a1=sim(net,p1)
p2=[1;-1],a2=sim(net,p2)
p3={[1;1] [1 ;-1]},a3=sim(net,p3) 
p4=[1 1;1 -1],a4=sim(net,p4)
net.IW{1,1}=[3,4];
net.b{1}=[1];
a1=sim(net,p1)

net=init(net);
wts=net.IW{1,1}
bias=net.b{1}
net.inputweights{1,1}.initFcn=‘rands‘;
net.biases{1}.initFcn=‘rands‘;
net=init(net);
bias=net.b{1}
wts=net.IW{1,1}
a1=sim(net,p1)

net=newp([-2 2;-2 2],1);
net.b{1}=[0];
w=[1 -0.8]
net.IW{1,1}=w;
p=[1;2];
t=[1];
a=sim(net,p)
e=t-a
help learnp
dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
w=w+dw
net.IW{1,1}=w;
a=sim(net,p)


P=[-0.5 1 0.5 -0.1;-0.5 1 -0.5 1];
T=[1 1 0 1]
net=newp([-1 1;-1 1],1);
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1});
%hold on;
%plotpv(P,T);
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1})
net.adaptParam.passes=3;
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpc(net.IW{1},net.b{1})
net.adaptParam.passes=6;
net=adapt(net,P,T)
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1},net.b{1})

plotpc(net.IW{1},net.b{1})
a=sim(net,p);
plotpv(p,a)

p=[0.7;1.2]
a=sim(net,p);
plotpv(p,a);
hold on;
plotpv(P,T);
plotpc(net.IW{1},net.b{1})

P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50]
T=[1 1 0 0 1];
net=newp([-40 1;-1 50],1);
plotpv(P,T);
hold on;
linehandle=plotpc(net.IW{1},net.b{1});
E=1;
net.adaptParam.passes=3;
while (sse(E))
    [net,Y,E]=adapt(net,P,T);
    linehandle=plotpc(net.IW{1},net.b{1},linehandle);
    drawnow;
end;
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
net=init(net);
net.adaptParam.passes=3;
net=adapt(net,P,T);
plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}

net=newp([-40 1;-1 50],1,‘hardlim‘,‘learnpn‘);
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net.adaptParam.passes=3;
net=init(net);
linehandle=plotpc(net.IW{1},net.b{1});
while (sse(e))
[net,Y,e]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
end;
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}

net=newp([-40 1;-1 50],1);
net.trainParam.epochs=30;
net=train(net,P,T);
pause;
linehandle=plotpc(net.IW{1},net.b{1});
hold on;
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);

p=[1.0 1.2 2.0 -0.8; 2.0 0.9 -0.5 0.7]
t=[1 1 0 1;0 1 1 0]
plotpv(p,t);
hold on;
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net=init(net);
while (sse(e))
[net,y,e]=adapt(net,p,t);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;

matlab运行结果：

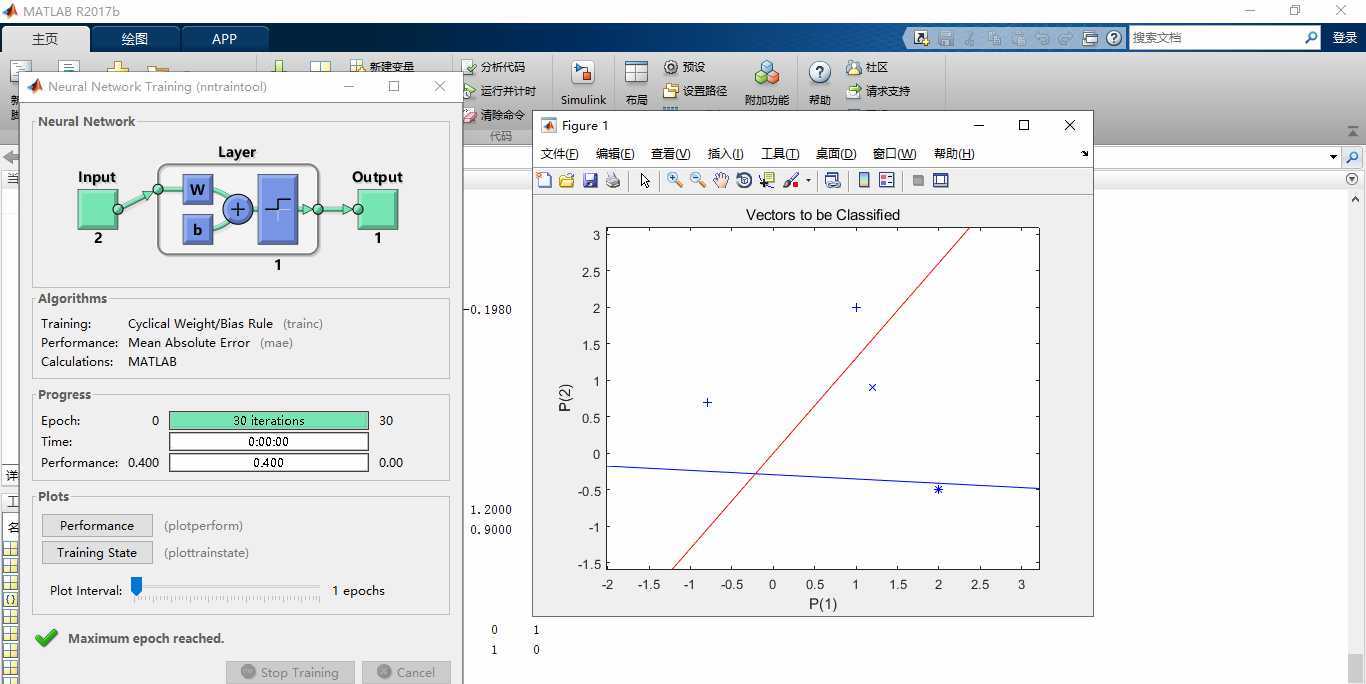
图：1

五、BP神经网络

（1）基本思想

BP神经网络也称为后向传播学习的前馈型神经网络，是一种典型的神经网络。后向传播是一种学习算法，体现为BP的训练过程，该过程是需要监督学习的；前馈型网络是一种结构，体现为BP的网络构架，如图2就是一个典型的前馈型神经网络.这种神经网络结构清晰，使用简单，而且效率也很高，因此得到了广泛的重视和应用。反向传播算法通过迭代处理的方式，不断的调整连接神经元的网络权重，使得最终输出结果和预期结果的误差最小。广泛应用于各种分类系统，他也包括了训练和使用两个阶段。

技术图片

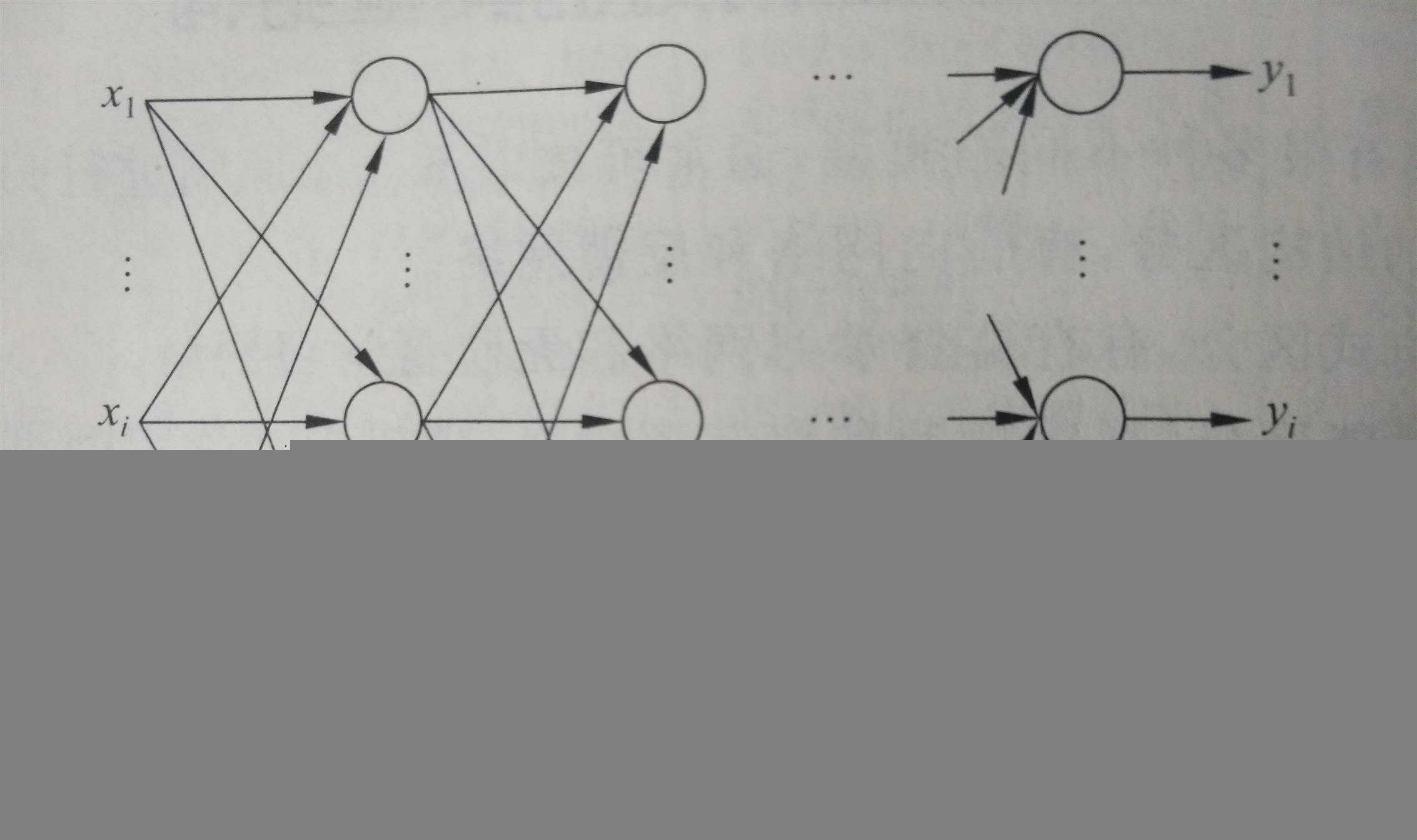
图：2

（2）算法过程

BP神经网络算法训练阶段的流程图和伪代码如下图所示：

技术图片

图：3

步骤一、初始化网络权重

步骤二、向前传播输入（前馈型网络）

步骤三、反向误差传播

步骤四、网络权重与神经元偏置调整

步骤五、判断结束

（3）BP神经网络代码实现

% BP网络
net=newff([-1 2;0 5],[3,1],{‘tansig‘,‘purelin‘},‘traingd‘)
net.IW{1}
net.b{1}

p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
%net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}

net.IW{1}
net.IW{2}
0.7616+net.b{2}
a-net.b{2}
(a-net.b{2})/ 0.7616
help purelin

p1=[0;0];
a5=sim(net,p1)
net.b{2}
net=newff([-1 2;0 5],[3,1],{‘tansig‘,‘purelin‘},‘traingd‘)
net.IW{1}
net.b{1}
%p=[1;];
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}

P=[1.2;3;0.5;1.6]
W=[0.3 0.6 0.1 0.8]
net1=newp([0 2;0 2;0 2;0 2],1,‘purelin‘);
net2=newp([0 2;0 2;0 2;0 2],1,‘logsig‘);
net3=newp([0 2;0 2;0 2;0 2],1,‘tansig‘);
net4=newp([0 2;0 2;0 2;0 2],1,‘hardlim‘);

net1.IW{1}
net2.IW{1}
net3.IW{1}
net4.IW{1}
net1.b{1}
net2.b{1}
net3.b{1}
net4.b{1}
net1.IW{1}=W;
net2.IW{1}=W;
net3.IW{1}=W;
net4.IW{1}=W;
a1=sim(net1,P)
a2=sim(net2,P)
a3=sim(net3,P)
a4=sim(net4,P)
init(net1);
net1.b{1}
help tansig
p=[-0.1 0.5]
t=[-0.3 0.4]
w_range=-2:0.4:2;
b_range=-2:0.4:2;

ES=errsurf(p,t,w_range,b_range,‘logsig‘);
pause(0.5);
hold off;
net=newp([-2,2],1,‘logsig‘);
net.trainparam.epochs=100;
net.trainparam.goal=0.001;
figure(2);
[net,tr]=train(net,p,t);
title(‘动态逼近‘)
wight=net.iw{1}
bias=net.b
pause;
close;
p=[-0.2 0.2 0.3 0.4]
t=[-0.9 -0.2 1.2 2.0]
h1=figure(1);
net=newff([-2,2],[5,1],{‘tansig‘,‘purelin‘},‘trainlm‘);
net.trainparam.epochs=100;
net.trainparam.goal=0.0001;
net=train(net,p,t);
a1=sim(net,p)
pause;
h2=figure(2);
plot(p,t,‘*‘);
title(‘样本‘)
title(‘样本‘);
xlabel(‘Input‘);
ylabel(‘Output‘);
pause;
hold on;
ptest1=[0.2 0.1]
ptest2=[0.2 0.1 0.9]
a1=sim(net,ptest1);
a2=sim(net,ptest2);

net.iw{1}
net.iw{2}
net.b{1}
net.b{2}

matlab运行结果：

技术图片

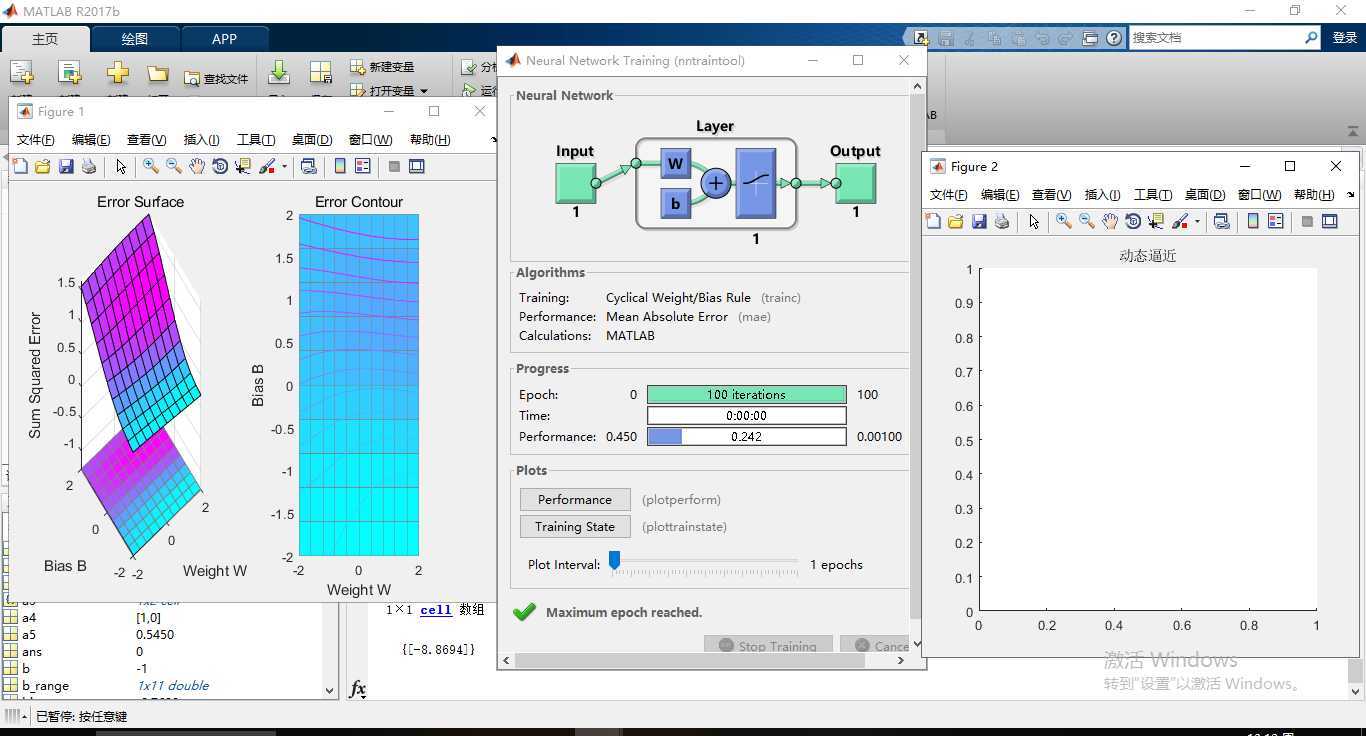
图：4

以上是关于感知机算法及BP神经网络的主要内容，如果未能解决你的问题，请参考以下文章