深度学习课程笔记神经网络基础
Posted 7TribeZ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了深度学习课程笔记神经网络基础相关的知识,希望对你有一定的参考价值。
目录
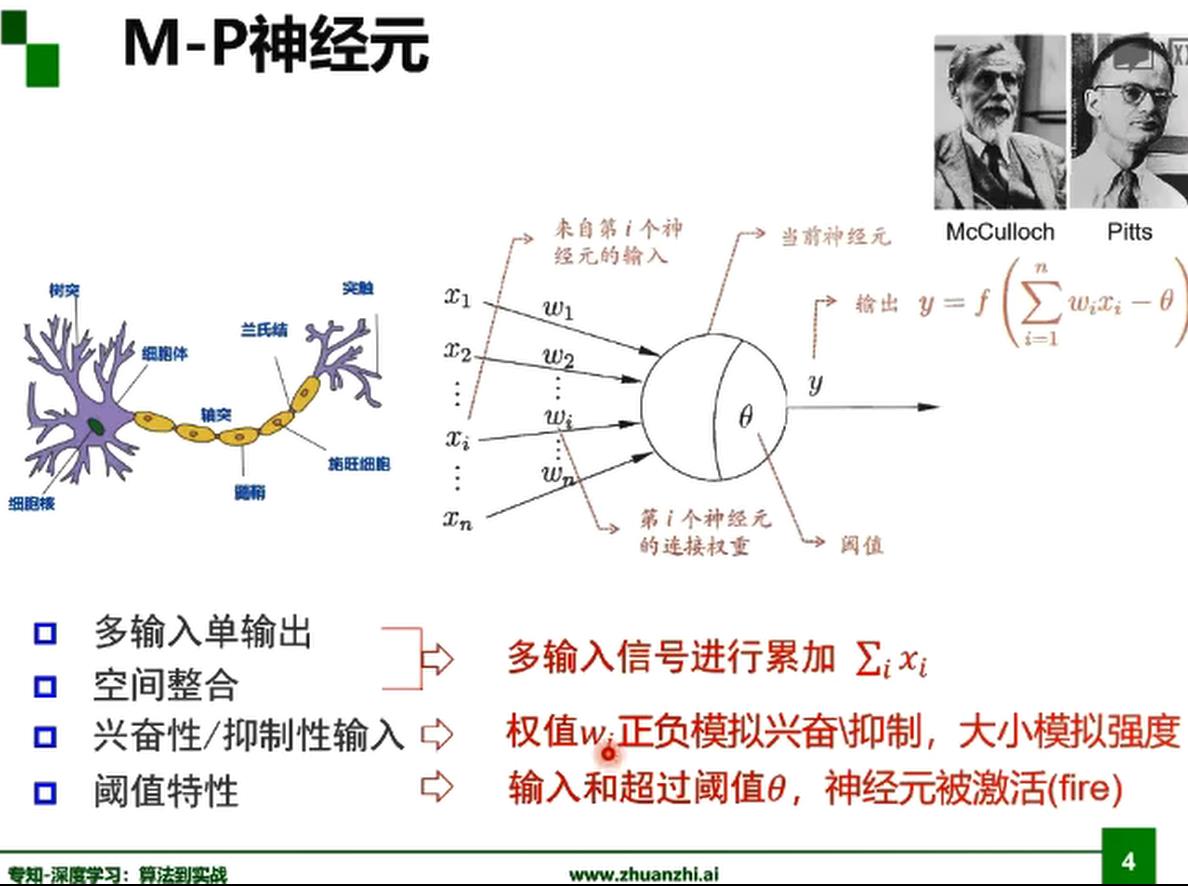
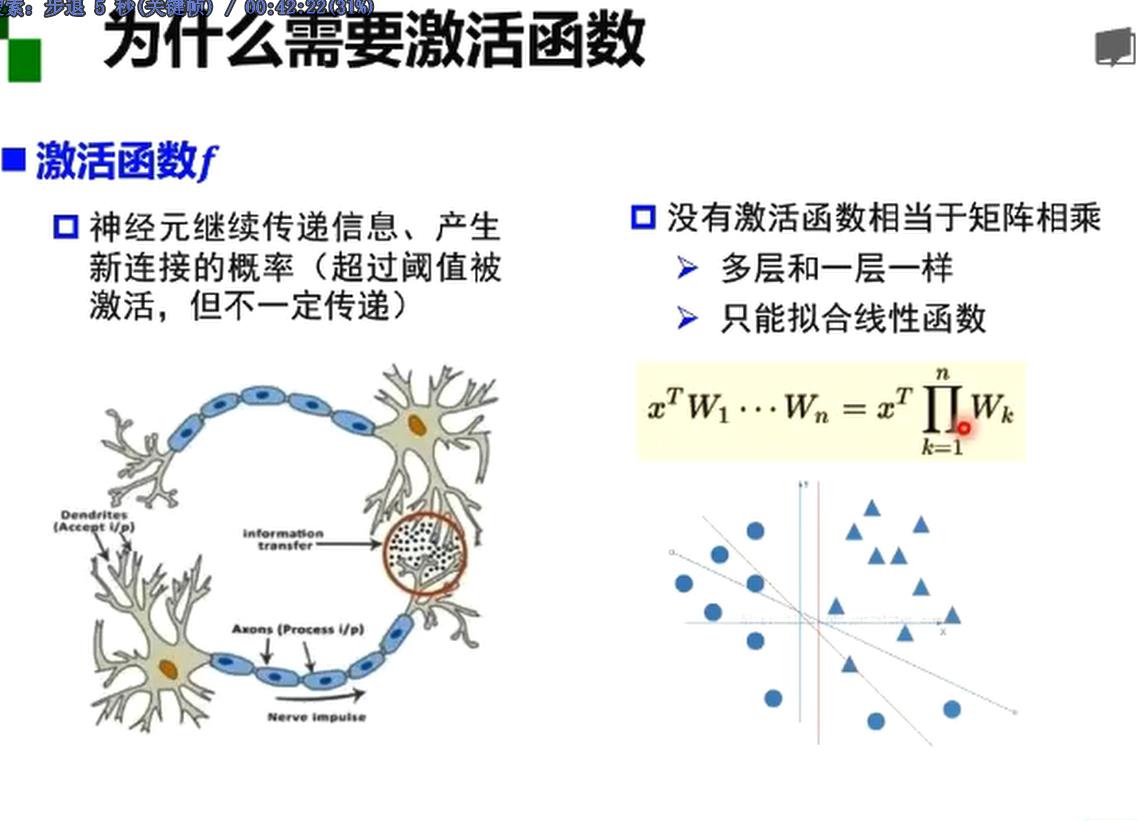
激活函数


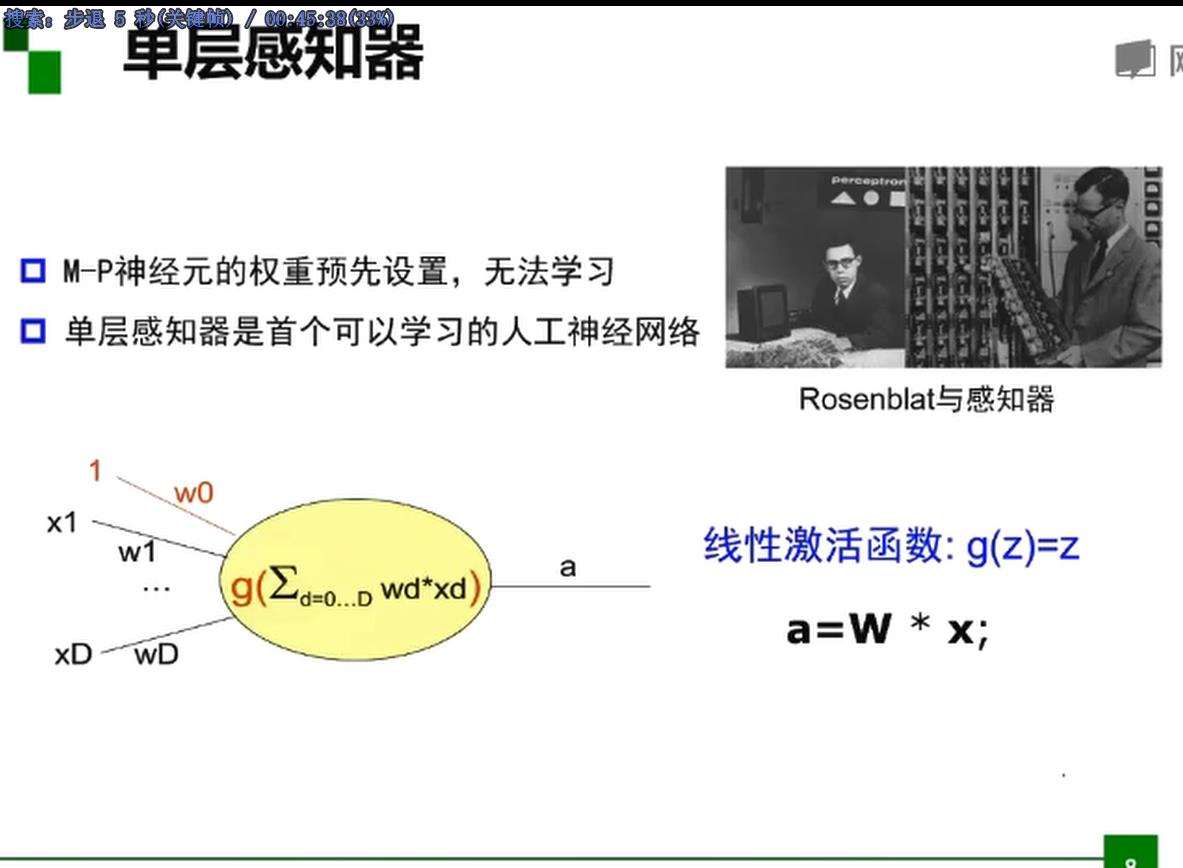
单层感知器
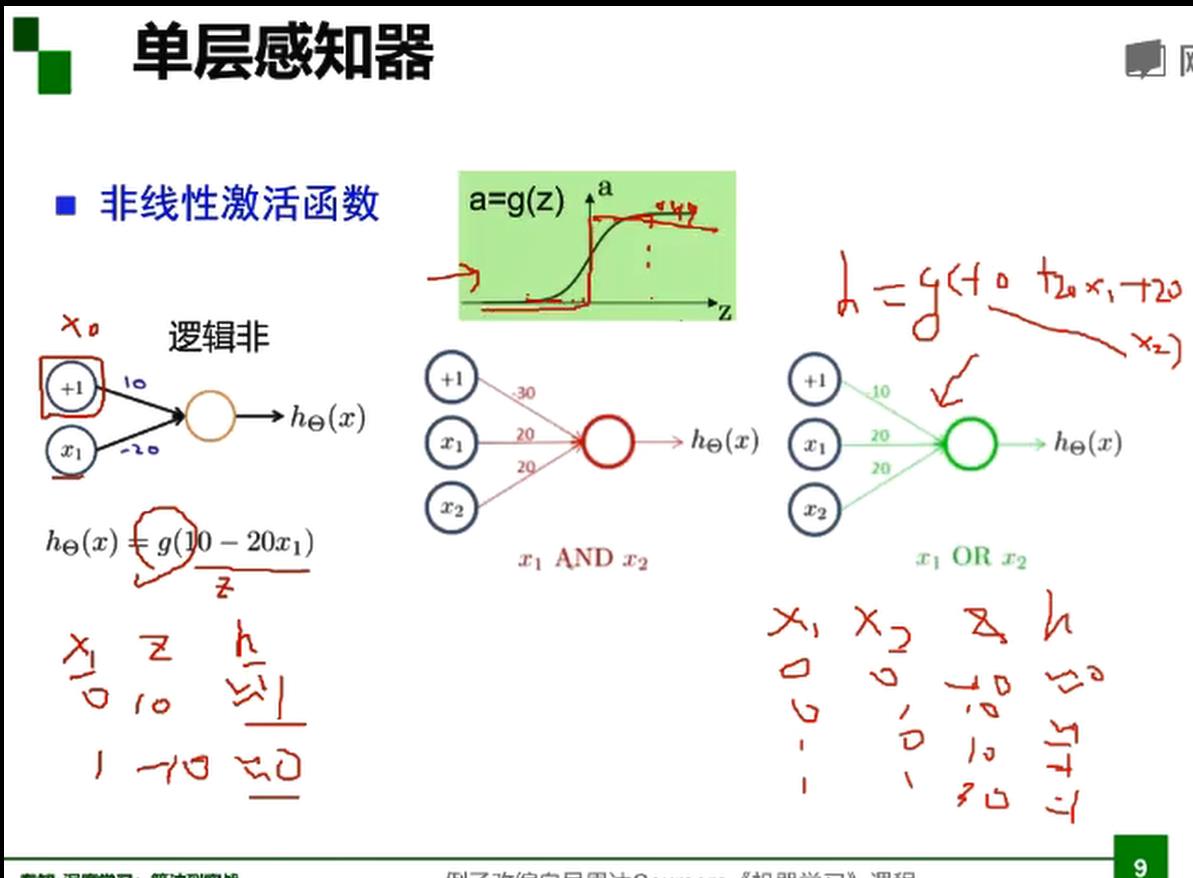
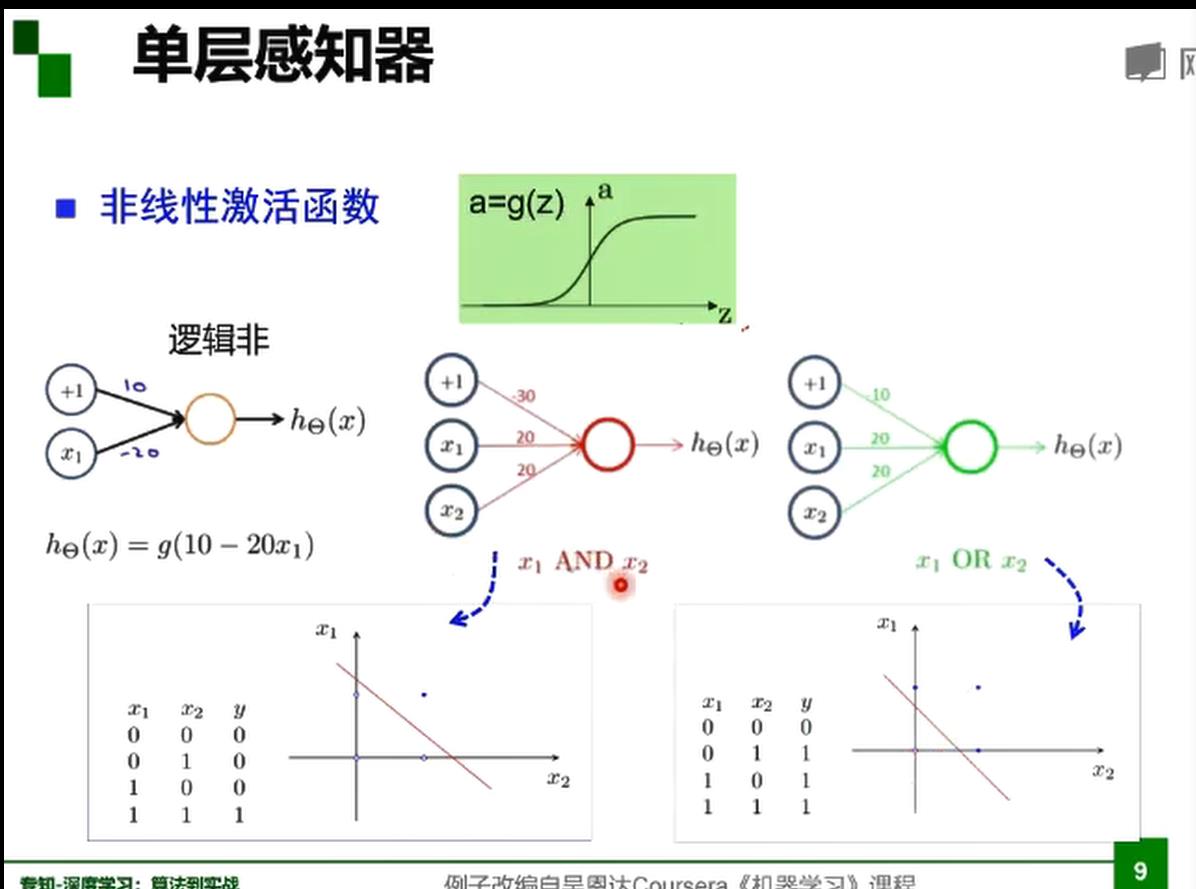
多层感知器
接下来解决非线性,如异或(单层感知机解决不了)

解决同或 非线性问题
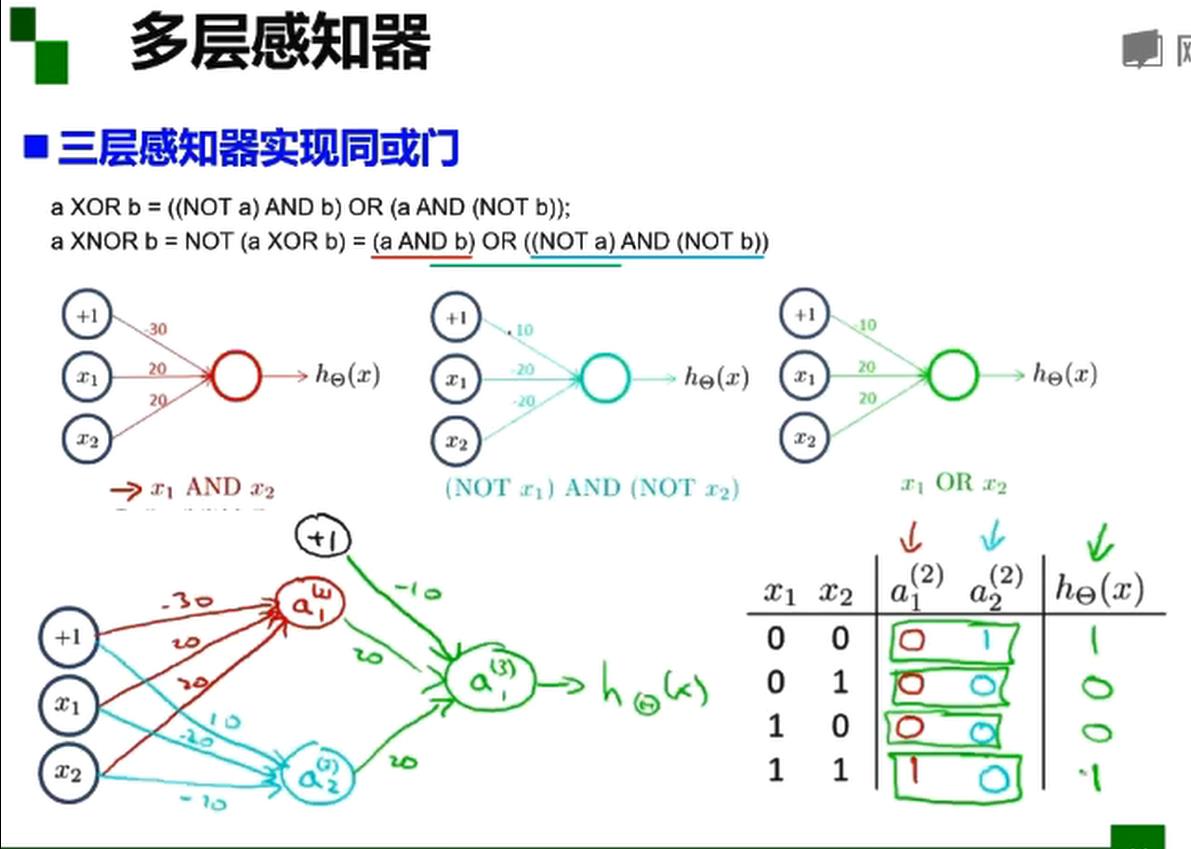
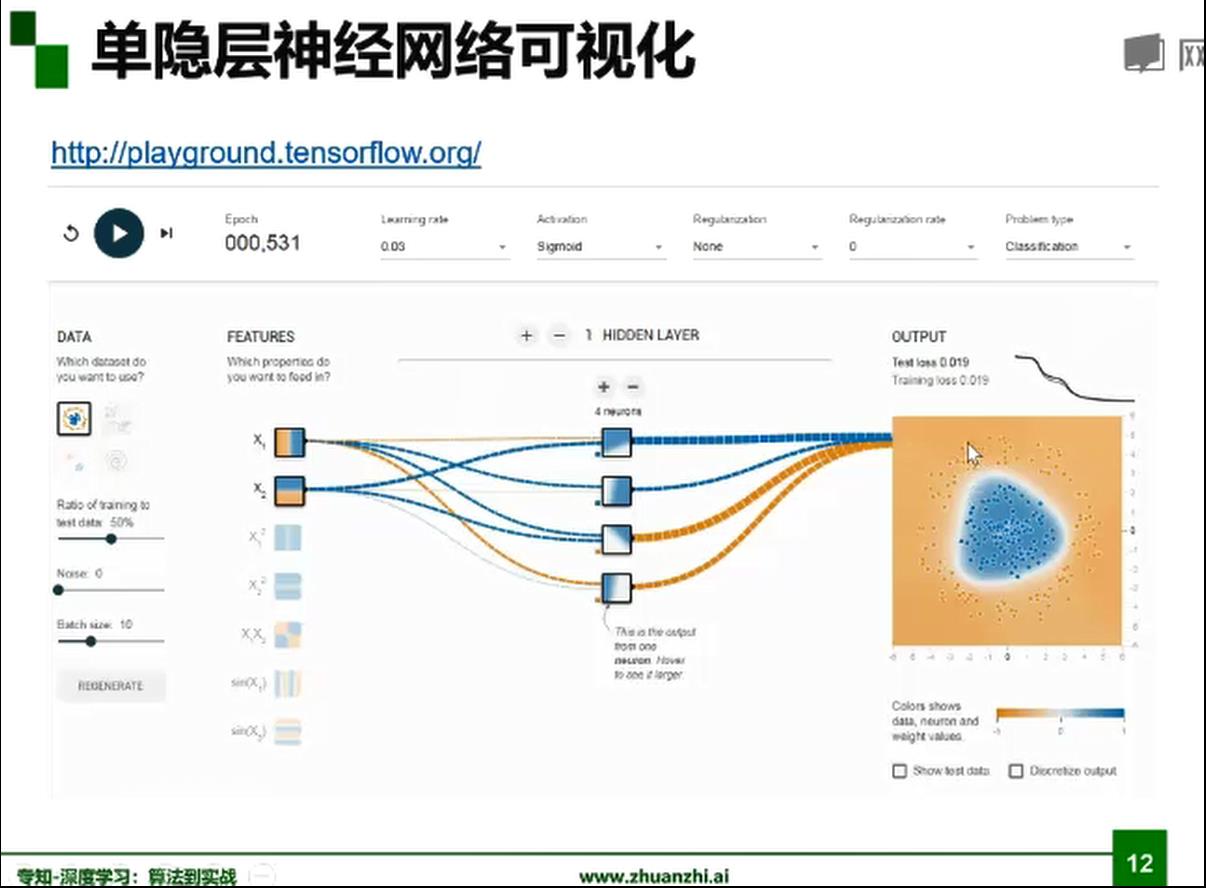
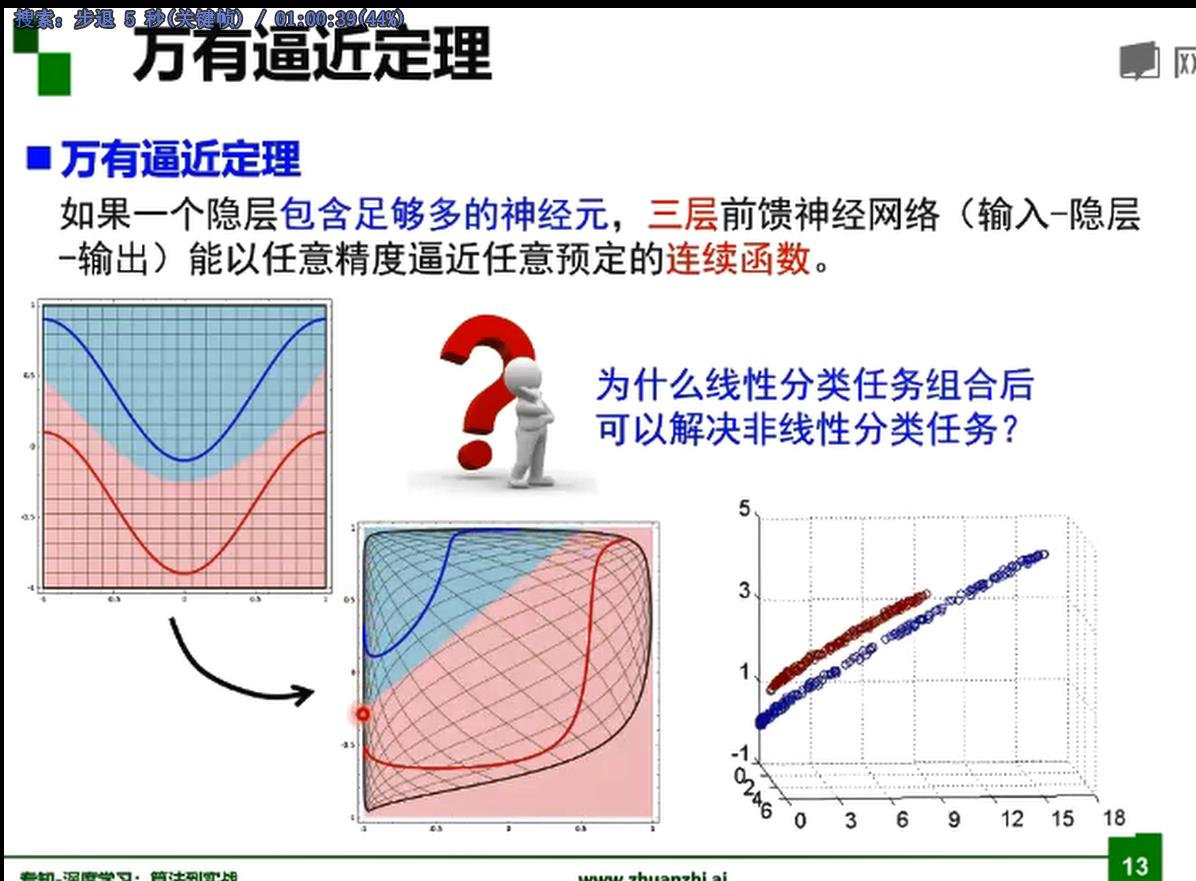
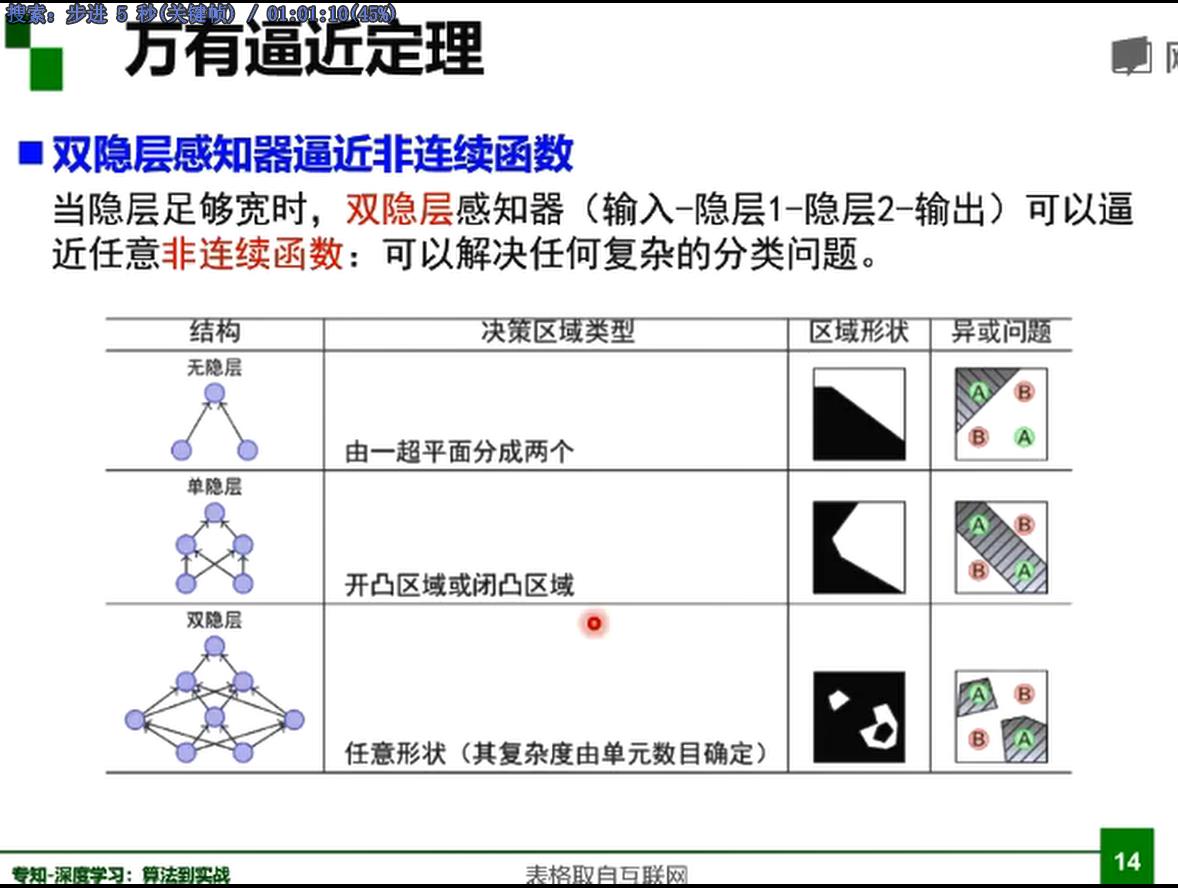

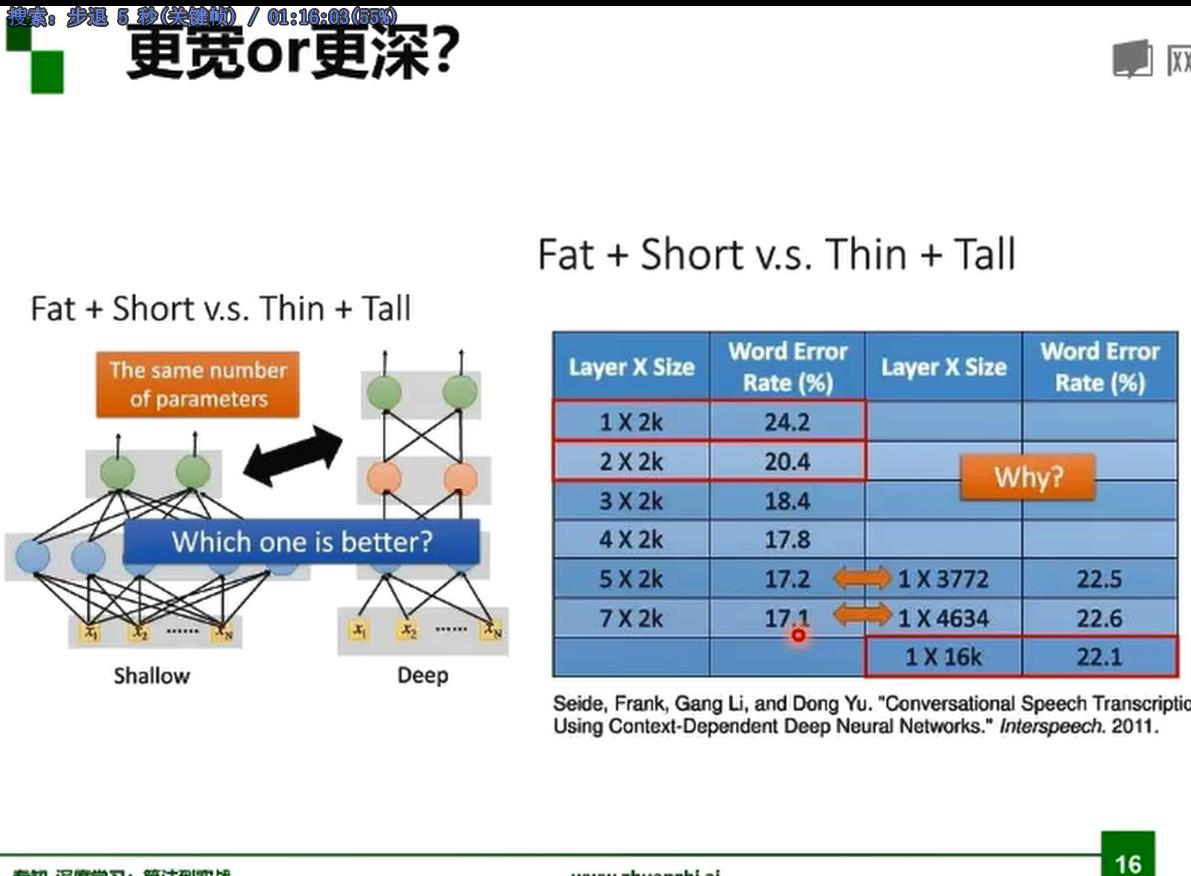

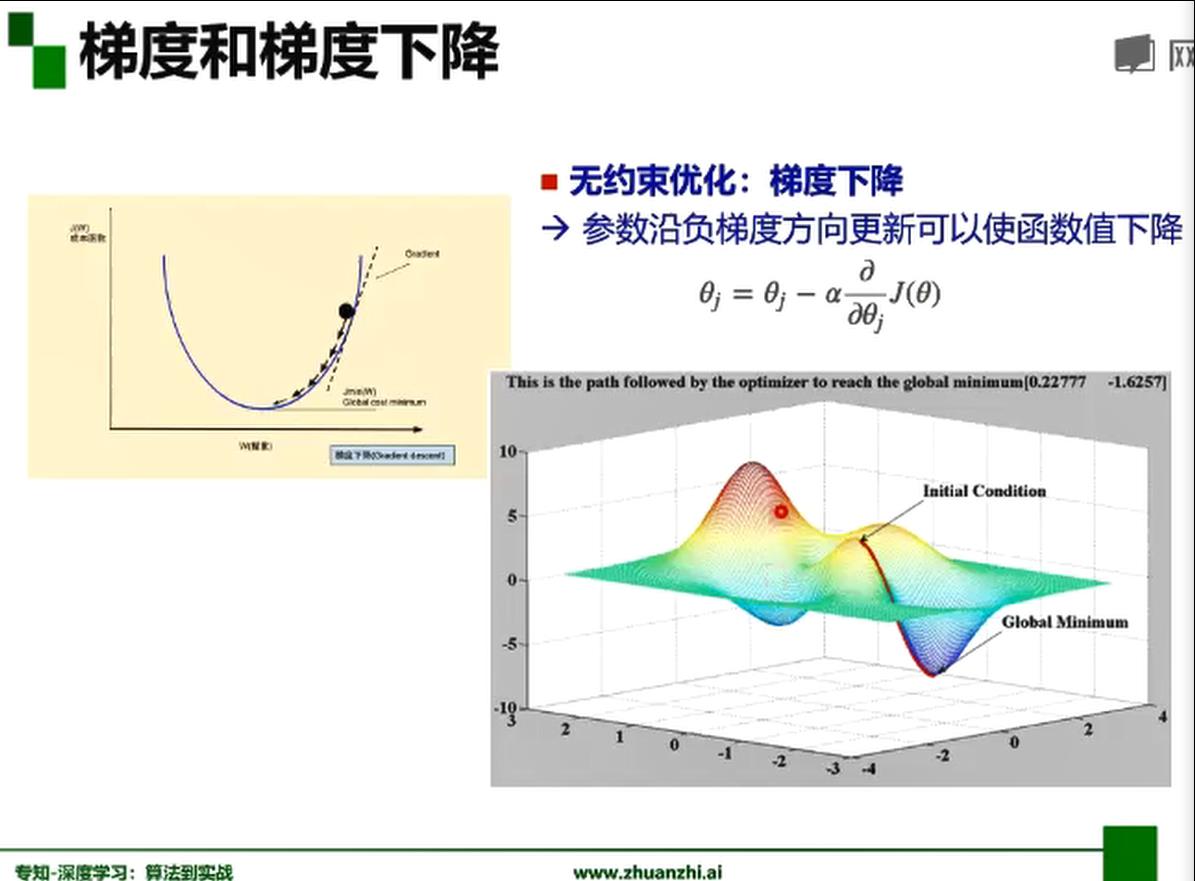
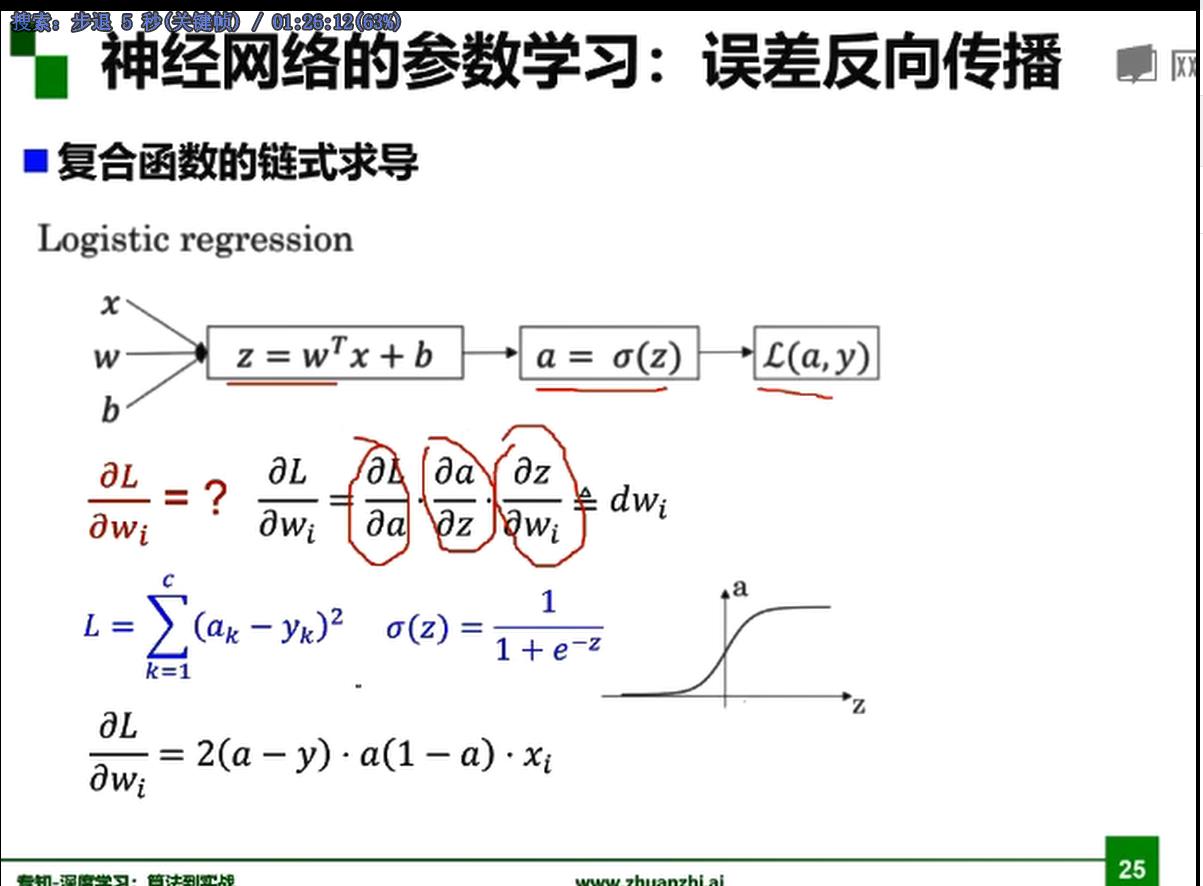
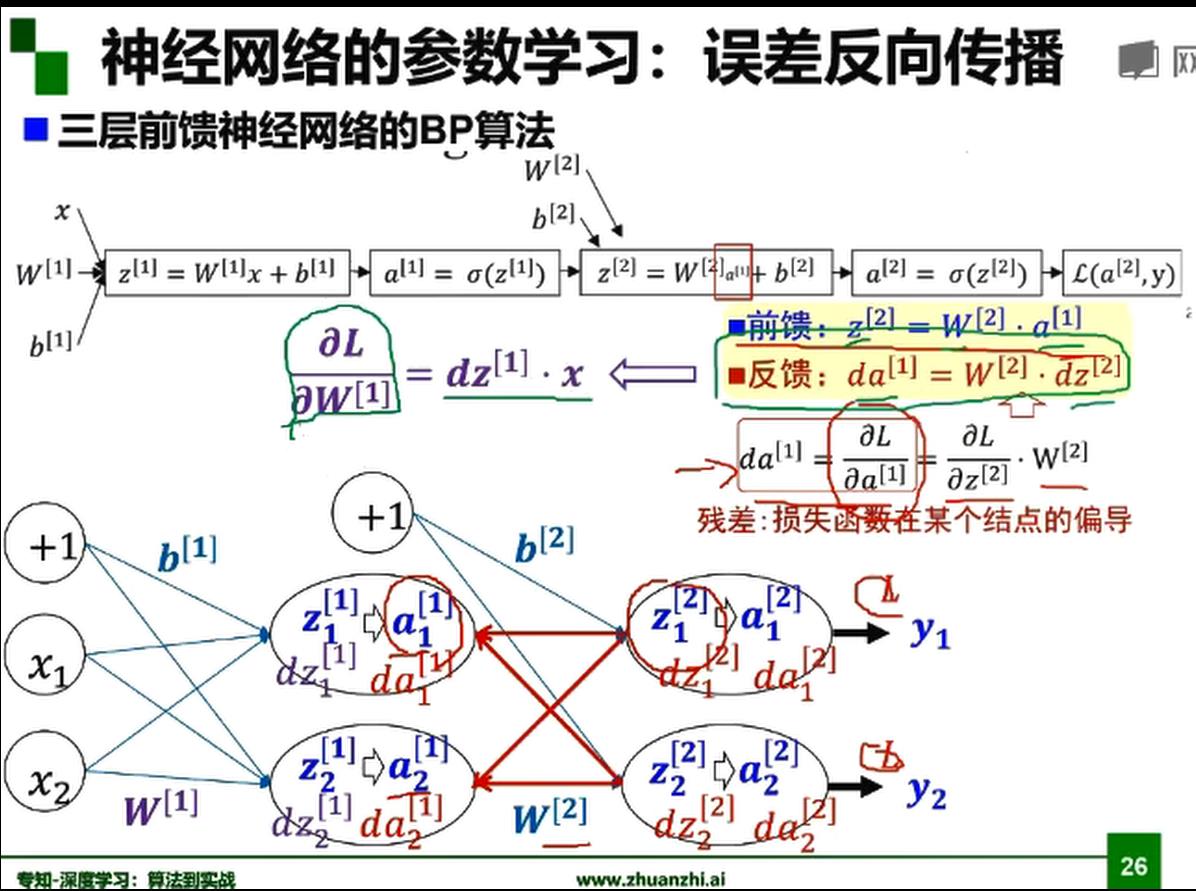
梯度下降,BP算法
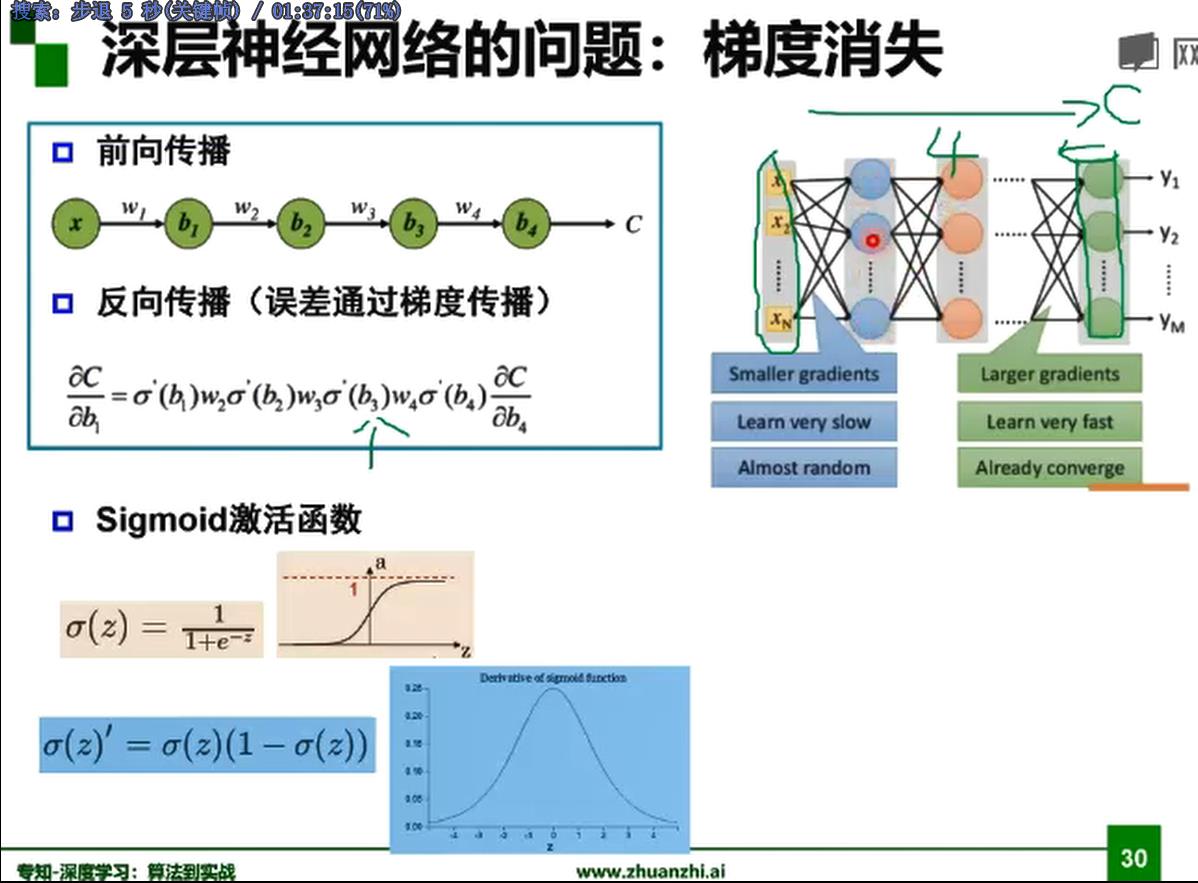
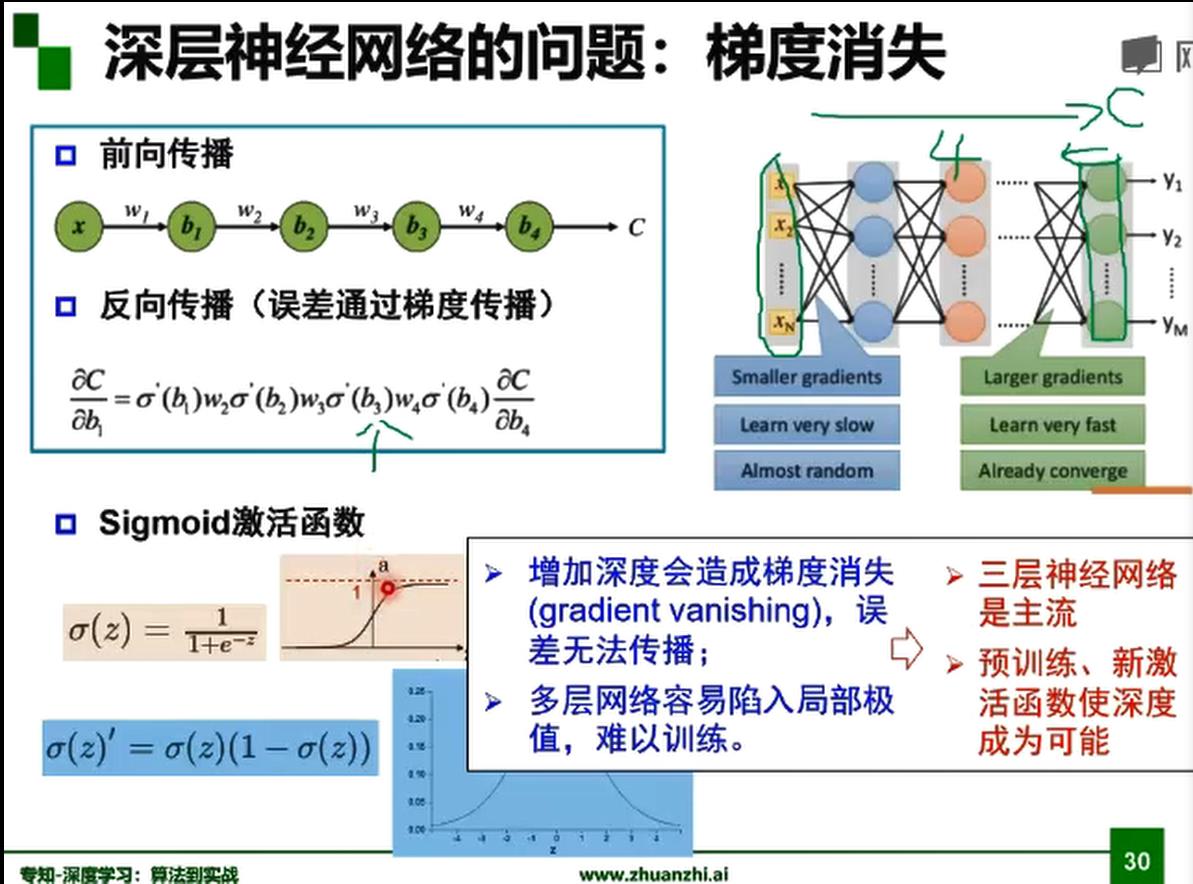
sigmoid函数梯度消失问题


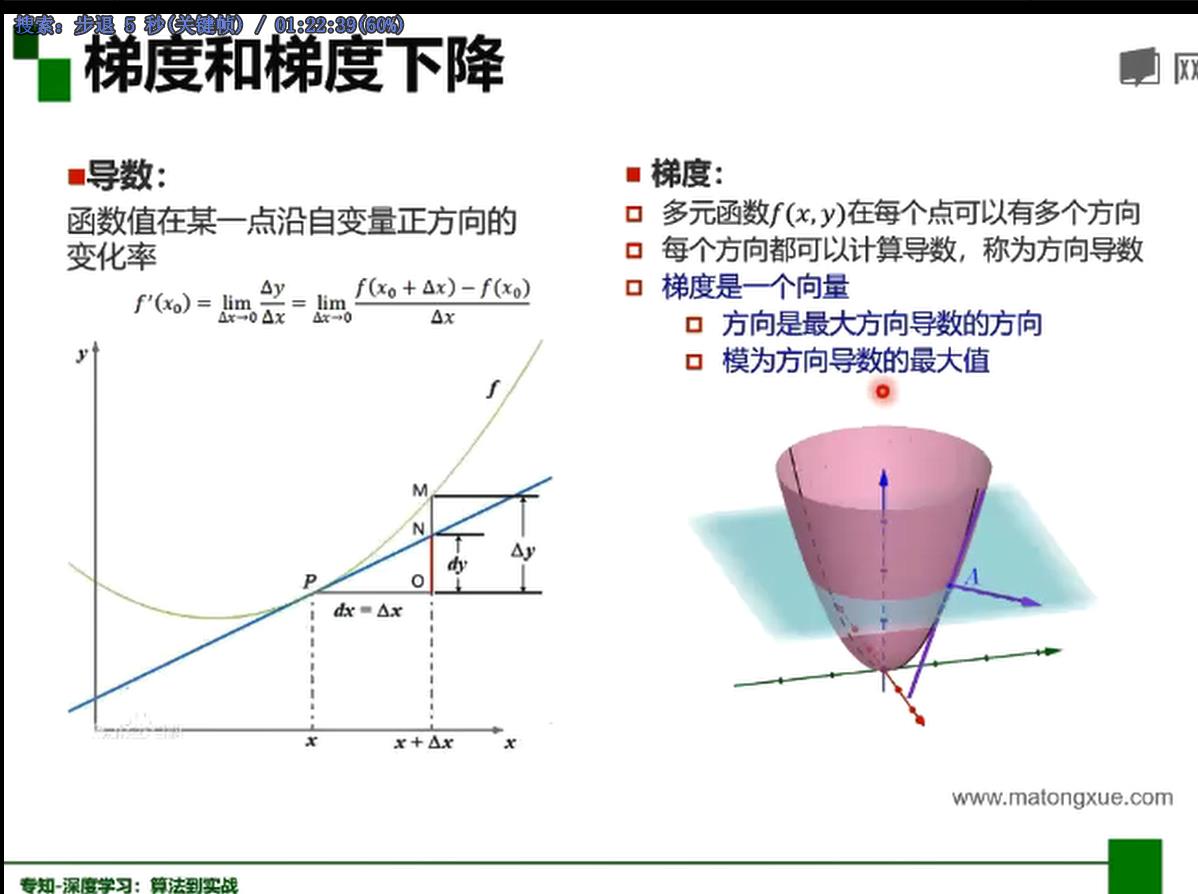
左图为凸函数可以找到全局的一个极值点,而右图是非凸函数,非常依赖初始值的选取,而决定是否找到全局的极值点。
梯度消失
由于 sigmoid 激活函数 的梯度容易落到饱和区,即趋向于0,在反向传播时,前面的节点由于计算梯度时,这个激活函数的导数趋向于0,导致梯度消失,而导致可能只能更新后面几层的参数,无法更新前面的节点。导致神经网络无法通过反向传播,梯度下降方法来更新参数。
逐层预训练
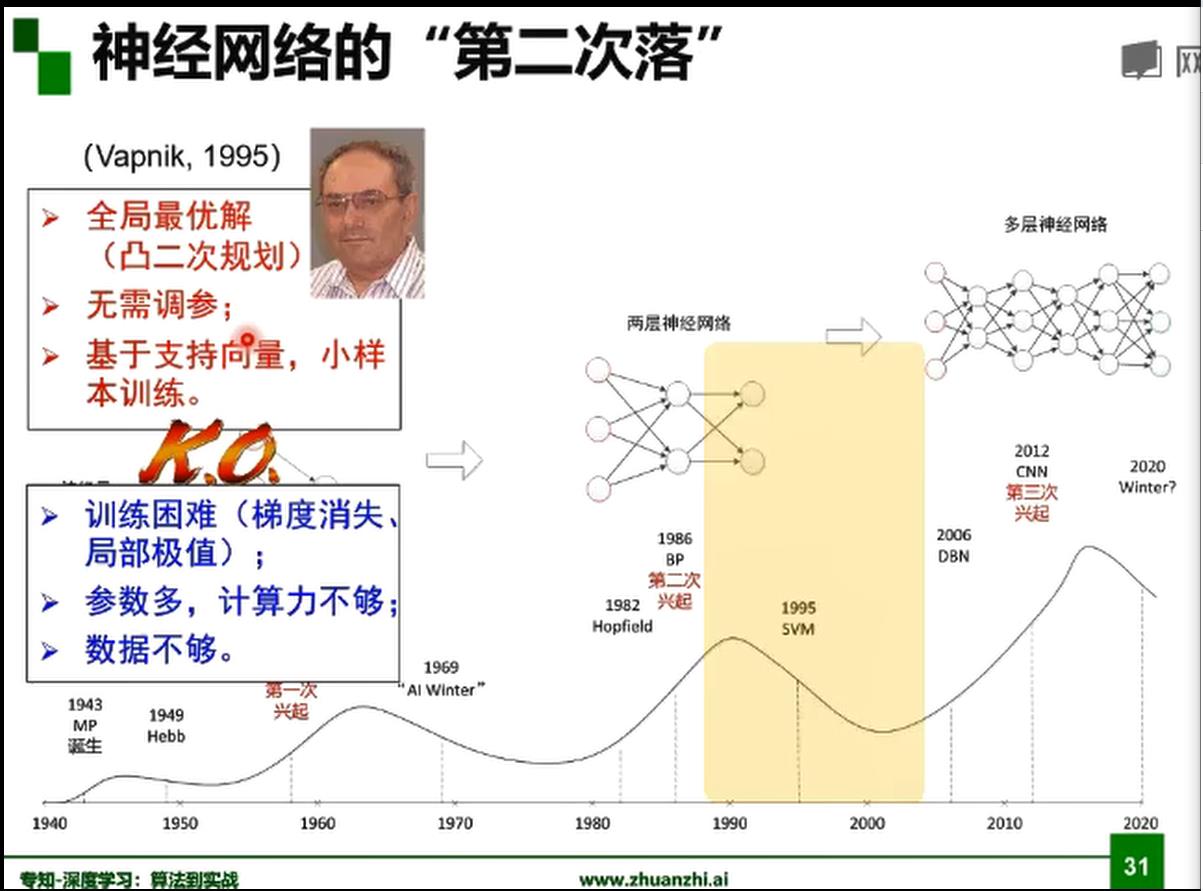
层数越高局部极小值最多,容易落到差的局部极小值。
预训练使得找到很好的初始值的参数。

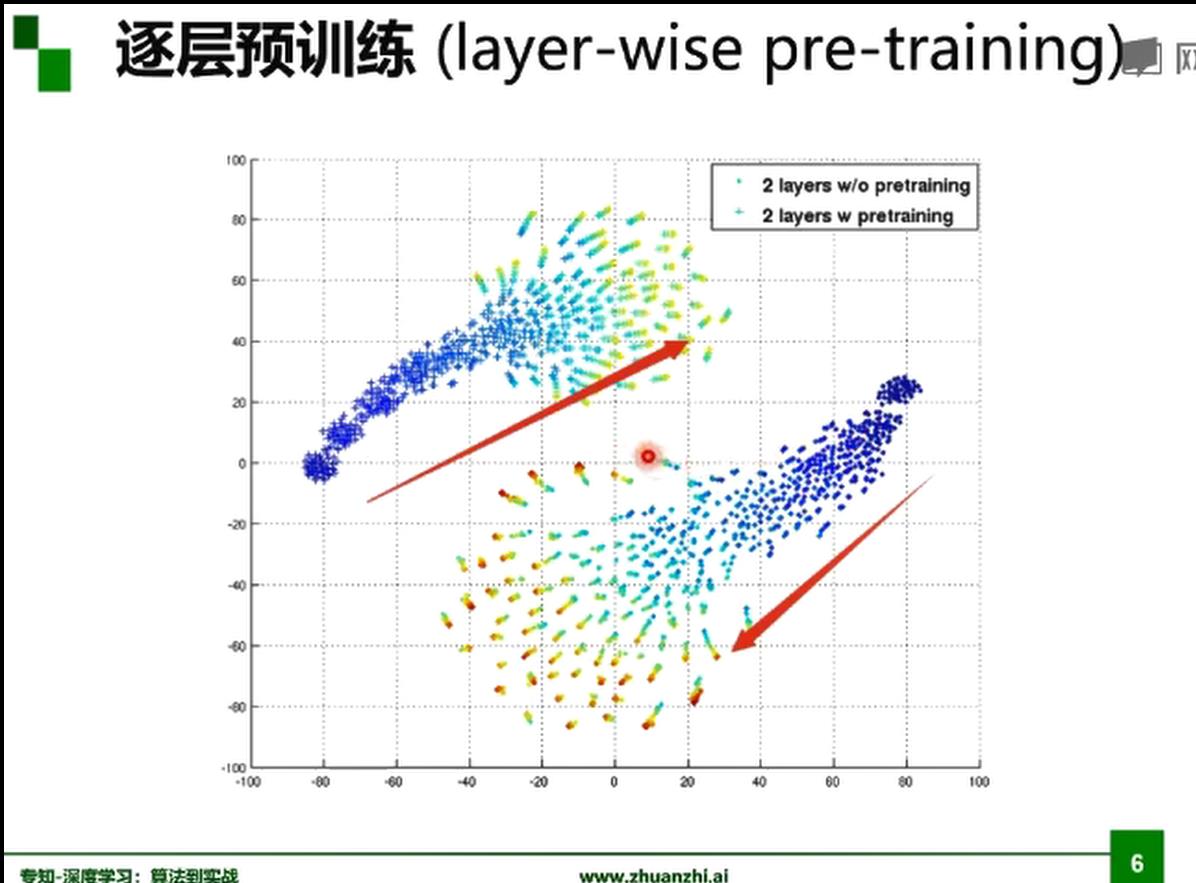
经过逐层预训练,解会相对收敛,不容易落到很差的点里。 二是训练会更快。(有一个保证,初始就不会太差)
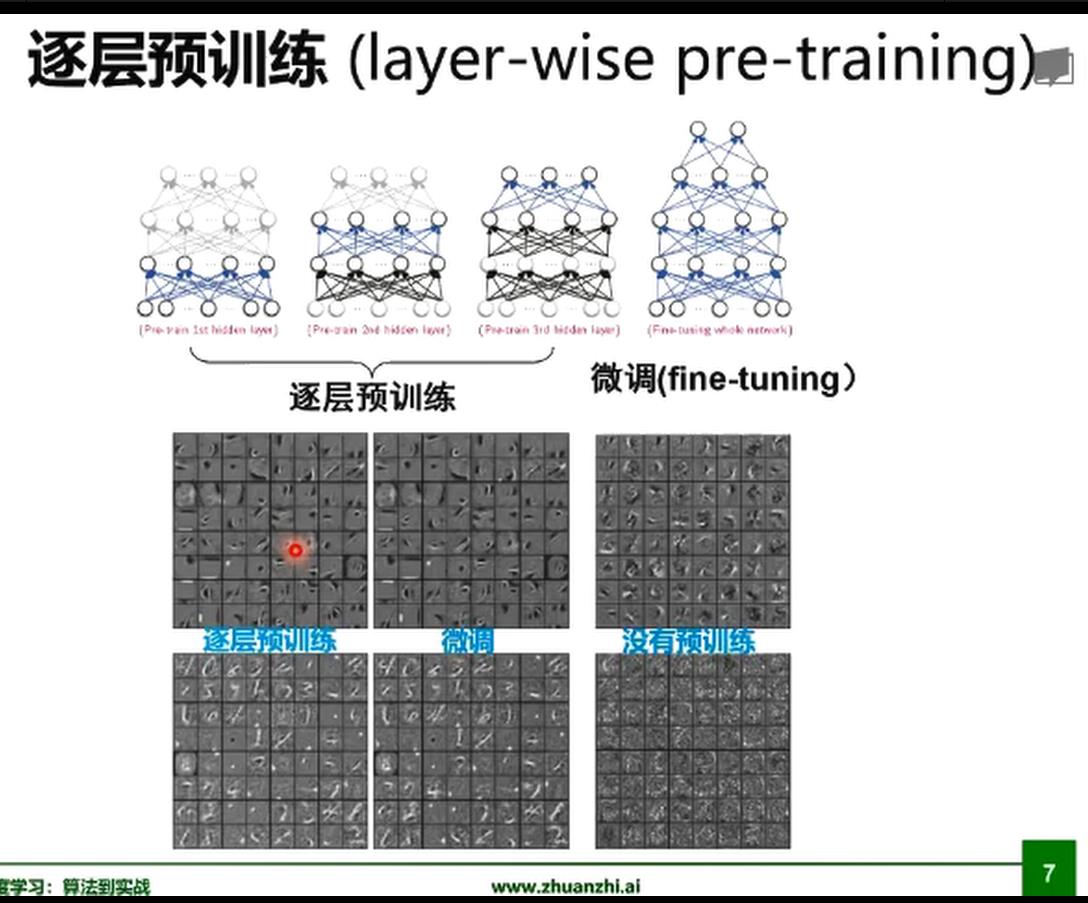
逐层预训练难点在于中间可能有很多隐层学习第一个隐层h1时是看不到y的,学习h5时才能看到y。即学习中间的隐层时,只有输入x,没有监督信息的。
两种方式 解决。
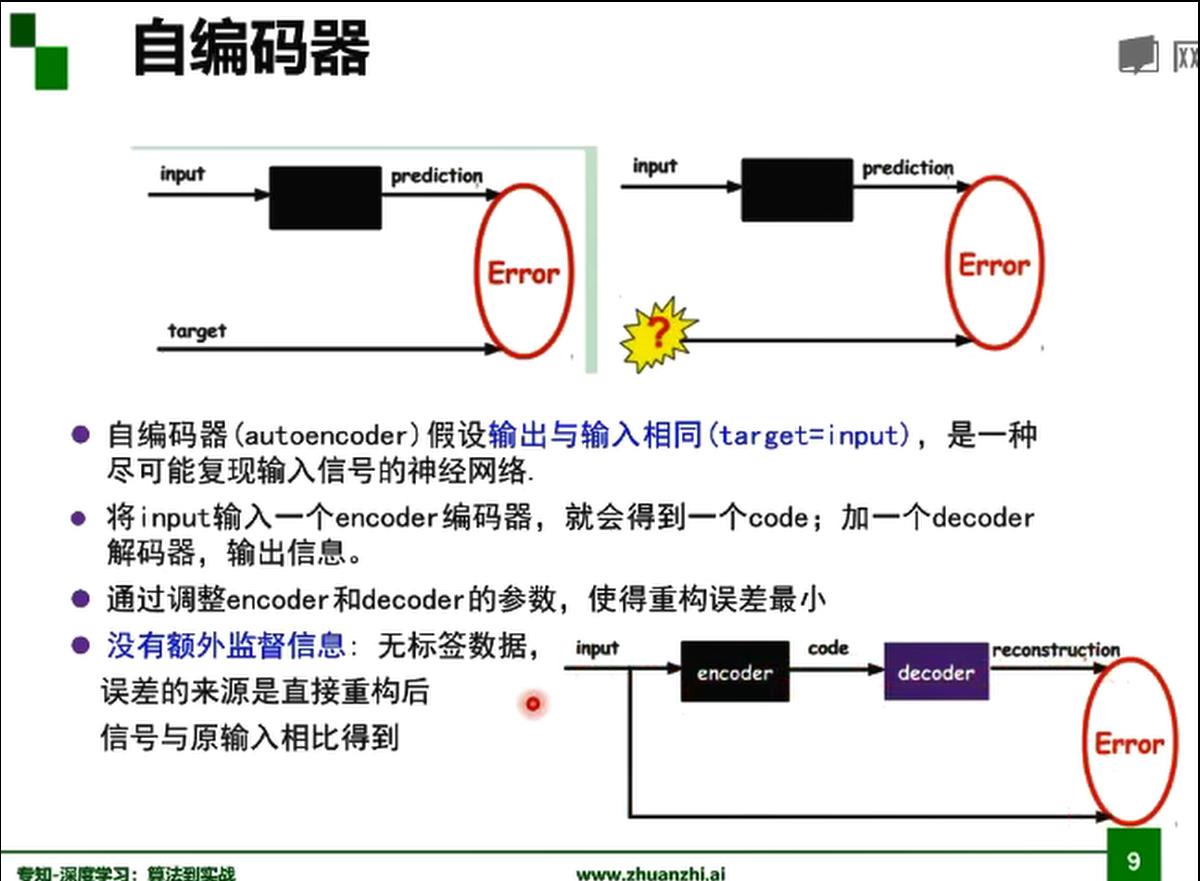
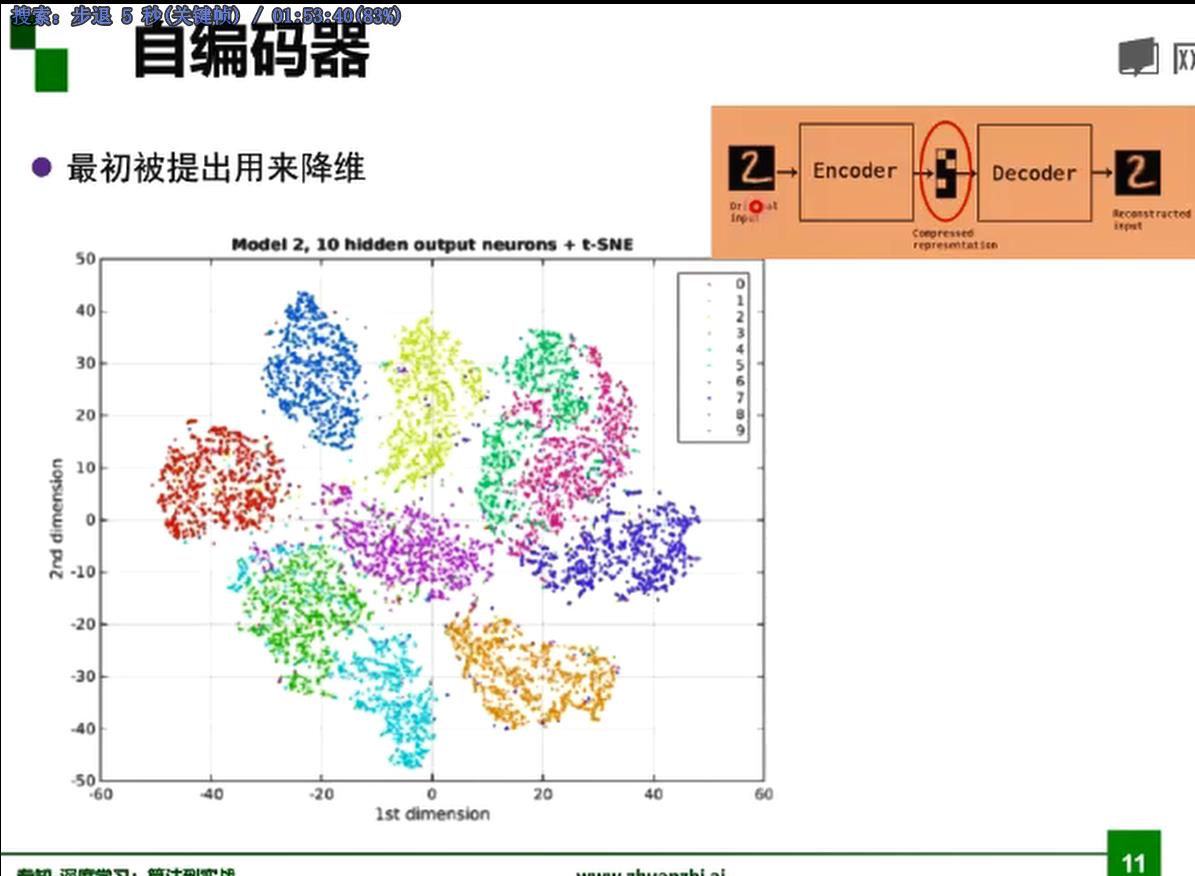
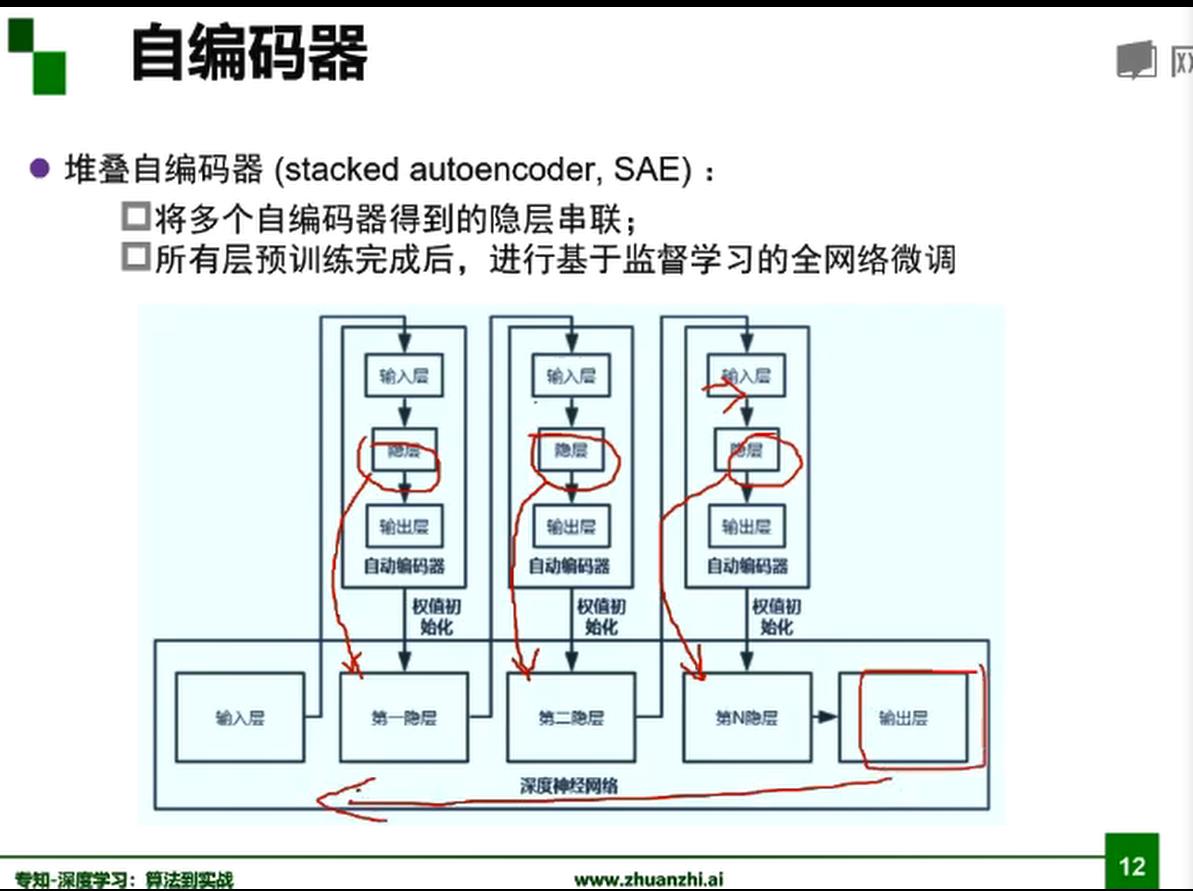
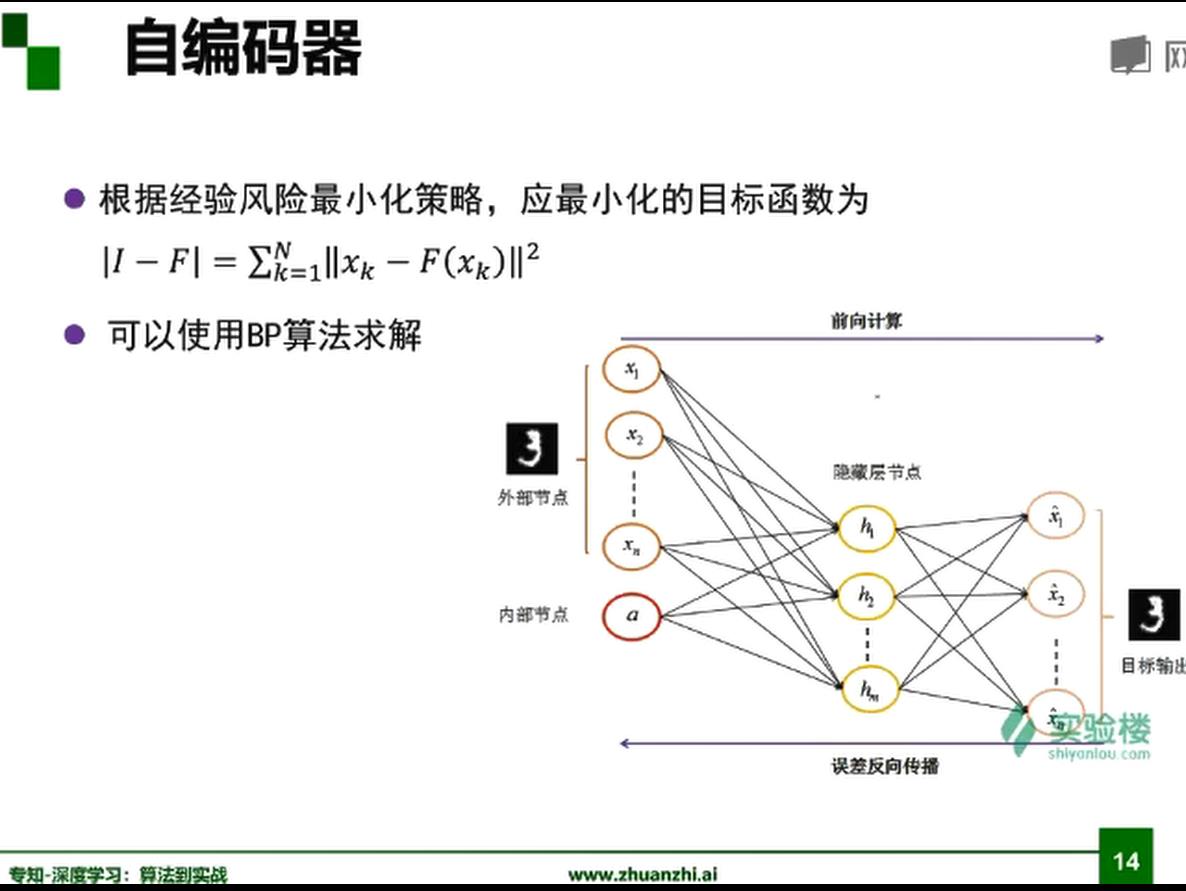
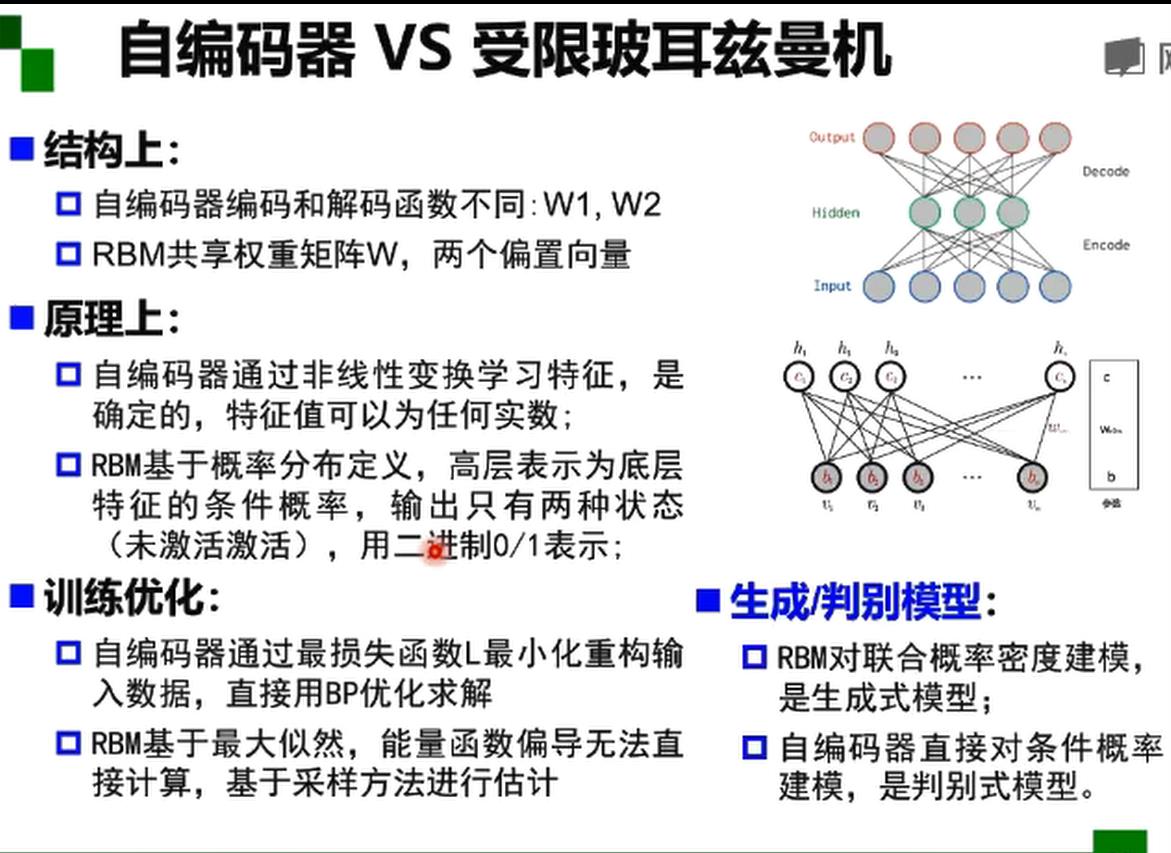
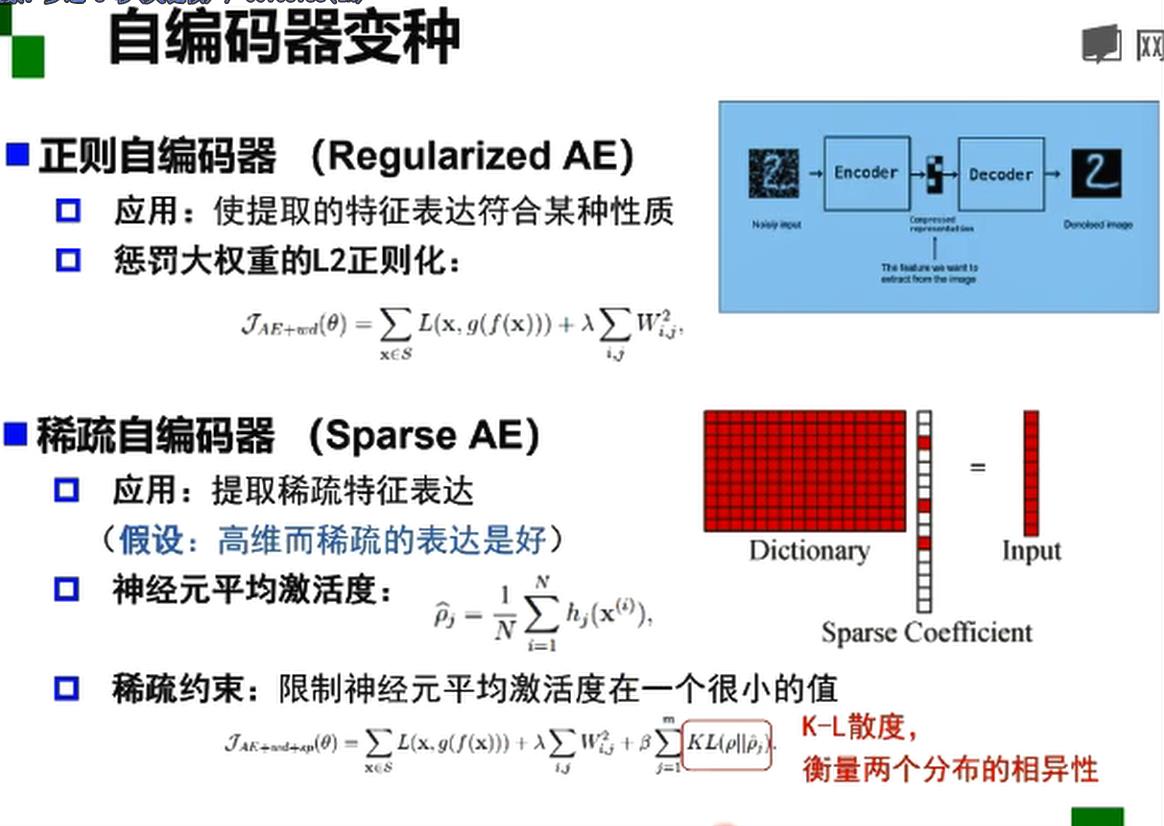
自编码器
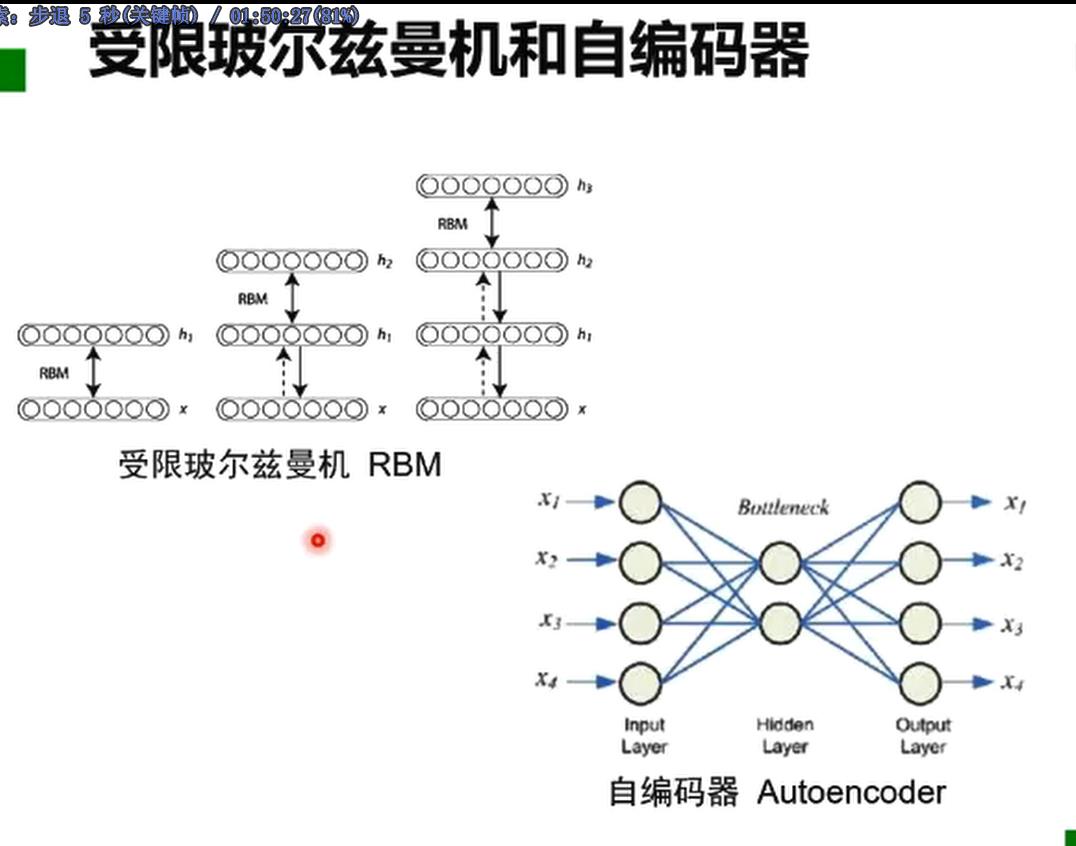
中间的编码就是想要学习的特征


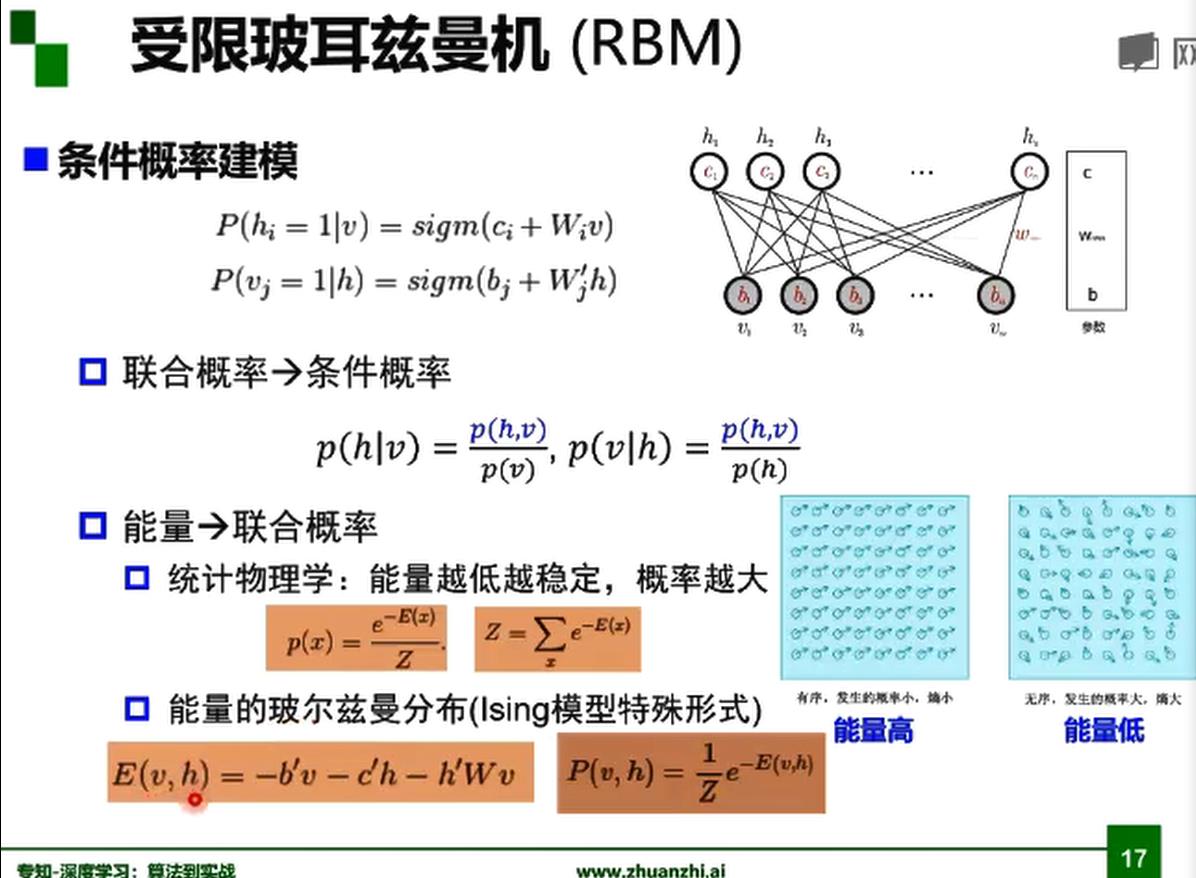
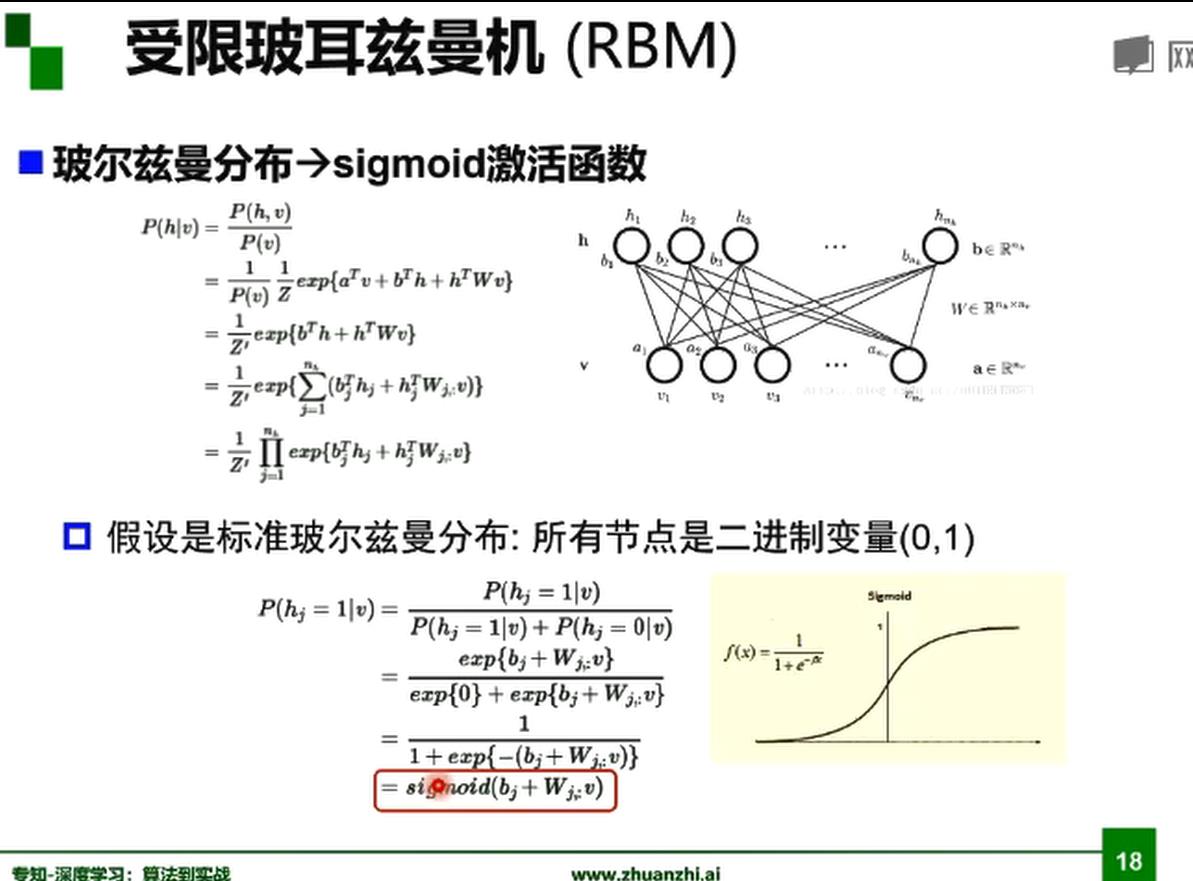
受限玻尔兹曼机RBM



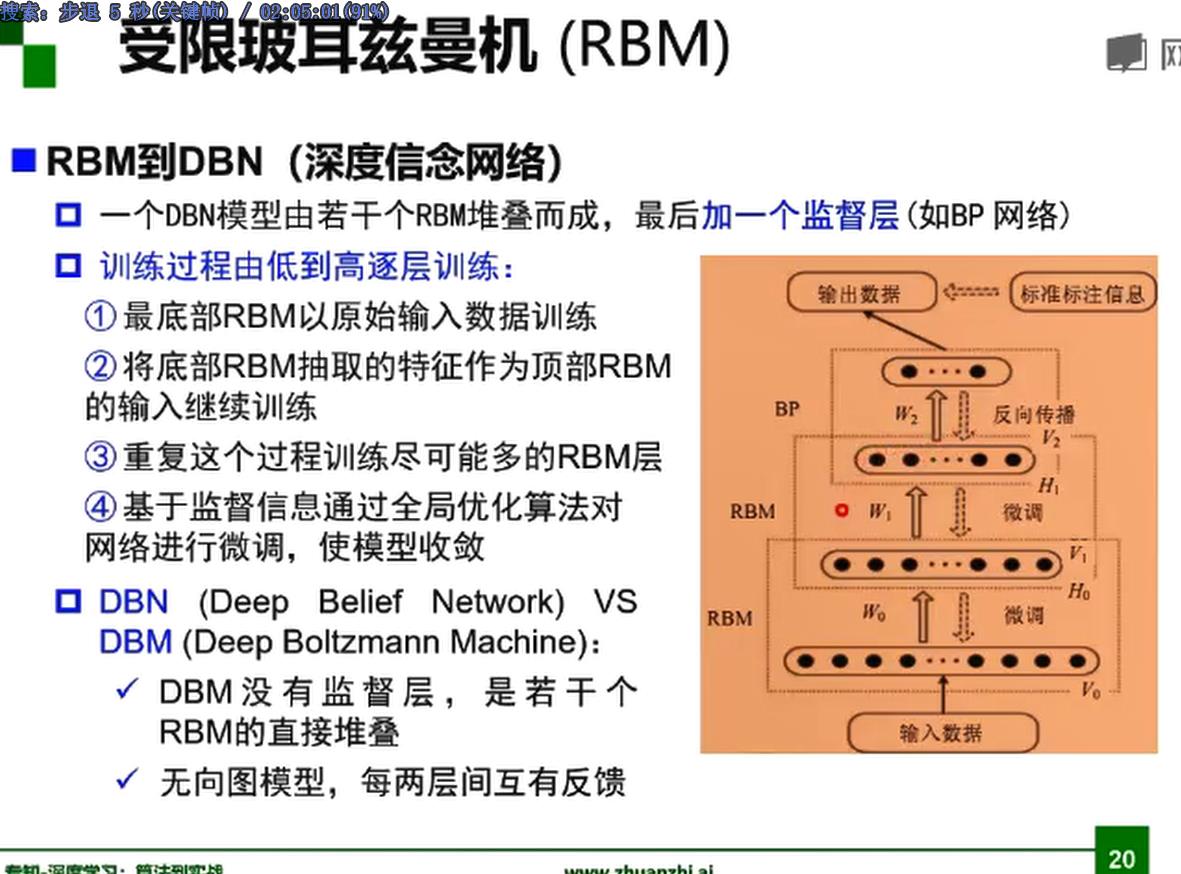
深度置信网络DBN,深度玻尔兹曼机DBM
一般玻尔兹曼机BM
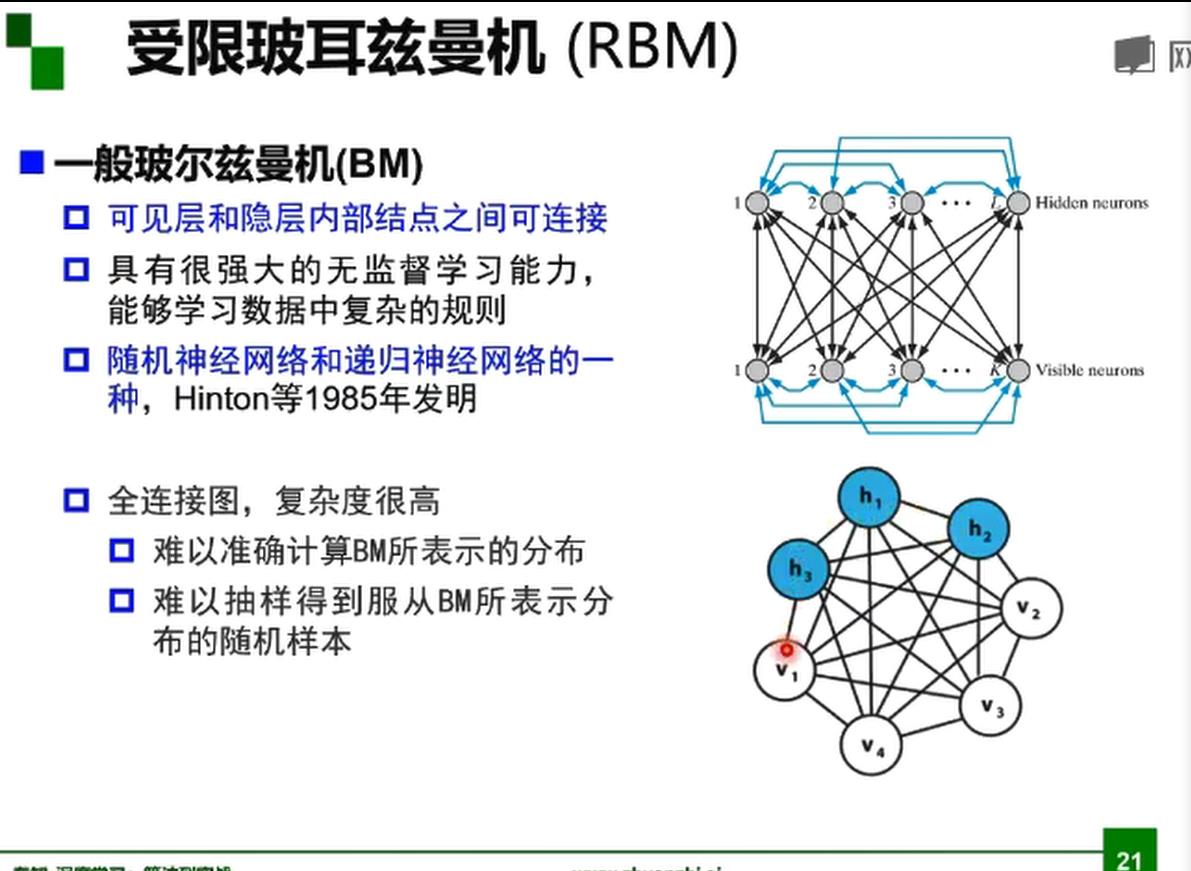
逐层预训练已经成为历史了
只是让初始值还不错,并没有根本解决梯度消失问题

解决梯度消失时间轴




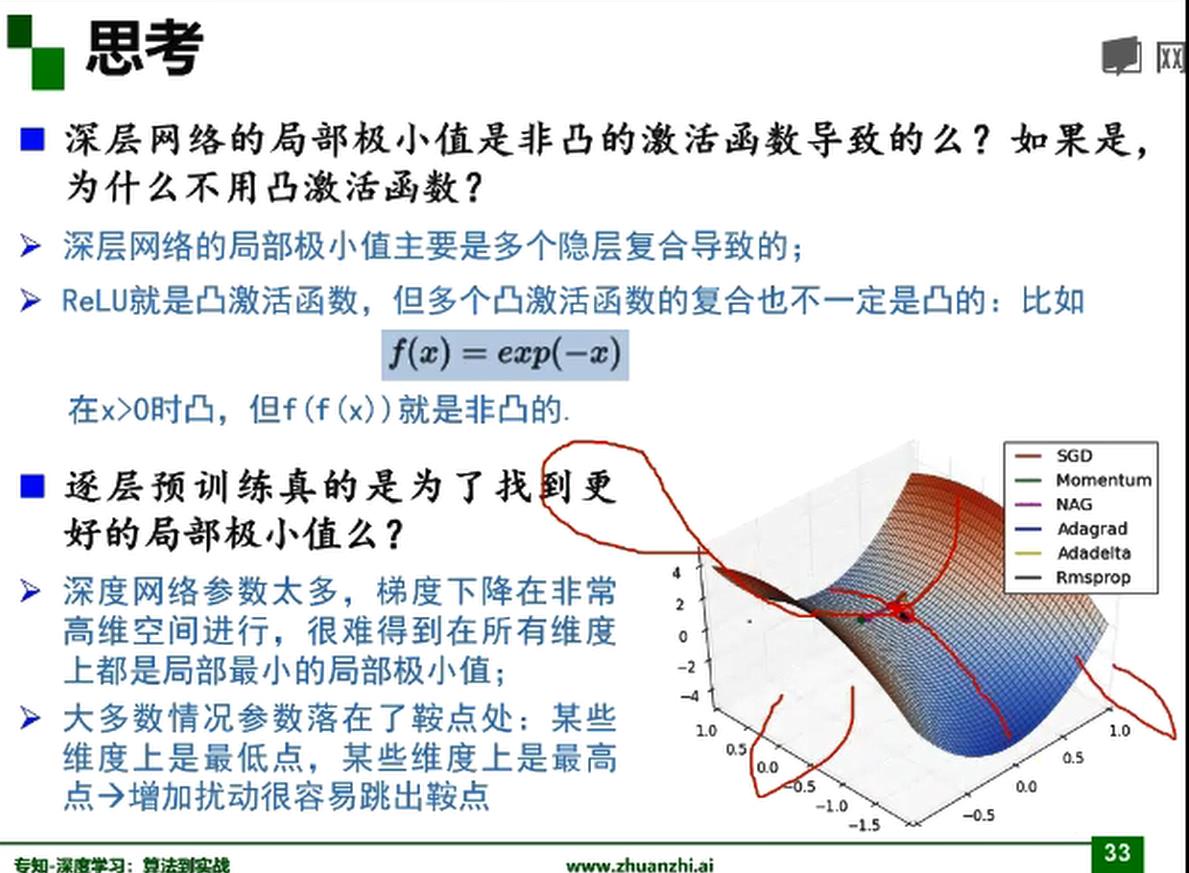
思考
下节预告

以上是关于深度学习课程笔记神经网络基础的主要内容,如果未能解决你的问题,请参考以下文章