网络流最大流——dinic算法

Posted 2021-03-08 jrdxy

前言

网络流问题是一个很深奥的问题，对应也有许多很优秀的算法。但是本文只会讲述dinic算法
最近写了好多网络流的题目，想想看还是写一篇来总结一下网络流和dinic算法以免以后自己忘了。。。

网络流问题简述

一个很普遍的例子就是——你家和自来水厂之间有许多中转站，中转站又由一些水管连接着。我们假设自来水厂的供水是无限的，并且中转站内能存储的水量也是无限的，但是管道有宽又窄，很显然管道内的流量必须小于等于管道的承载范围(否则管道就被撑爆了)，那么问题就是要你求出你家最多能收到多大流量的水。

emmm可能语言还是不好描述(个人表达能力太差)，还是给一道模板题吧。。。
https://www.luogu.com.cn/problem/P3376

用于解决网络流的算法有很多，EK，HLPP，dinic，ISAP......本文只讨论dinic算法(还不是因为我太菜了写不出来HLPP)

基本概念

基本概念还是要提一下的
源点：简单来说就是自来水厂
汇点：简单来说就是你家
容量：就是水管的承载范围，我们用c(u,v) (capacity)来表示
流量：此时水管里面水的流量，我们用f(u,v) (flow)来表示
弧：网络流中对有向边的简称
网络流图：有向图G=(V,E)中，有唯一的远点S,y有唯一的汇点T,并且每一条弧的容量都非负
可行流：对于弧(u,v)来说，f(u,v)<=c(u,v)，我们就称f(u,v)是可行流，意思就是流量<=容量，否则水管就被撑爆了
前向弧：从u指向v的一条有向边
反向弧：从v指向u的一条有向边
增广路：从S到T的一条简单路径，并且路径上的任意弧都是可行流，反向弧f(u,v)=0
暂时就说这么多吧。。。
肯定还是一脸懵逼的，那么我们现在正是开始介绍dinic算法

网络流算法

最经典的网络流算法通过不停地寻找增广路来计算最大流。还是非常好理解的，因为水会流到它能流到的任何地方。但是我们会遇到一个问题：

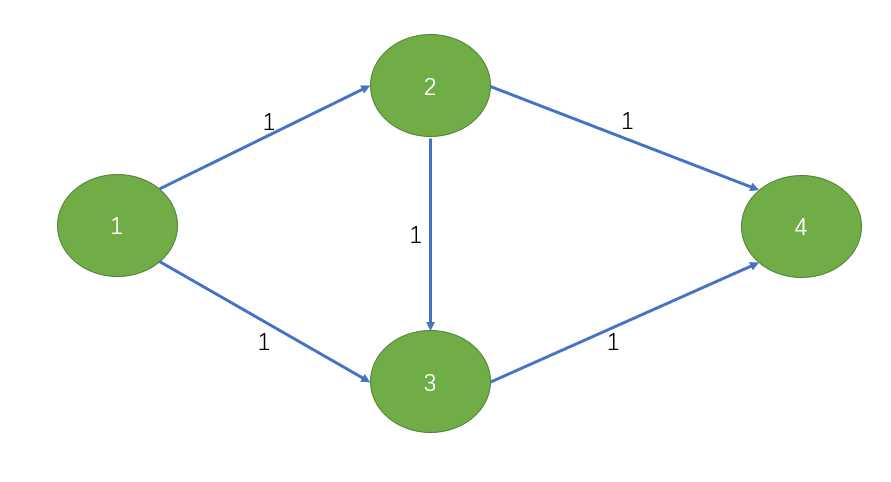
对于这副图来说，它的最大流很明显肯定是2，因为我们走1->2->4和1->3->4这两条增广路时每条增广路的流量都是1，所以最终算出来的总和是2。但是如果我们第一次就走1->2->3->4这条增广路的话，我们会发现，我们接下来无法在图上继续增广。因为仅凭1->3,2->4这两条弧不能让1和4连通。

所以，我们要做的就是为每一条边建立一个反边，用来使某些增广路“反悔”到它一开始的地方
由于反边并不是一条实际模型里面存在的边，所以初始化的话就是c‘(u,v)=c(u,v),f‘(u,v)=0
像这样，蓝色的是正常弧，红(橙？)色的是反向弧：

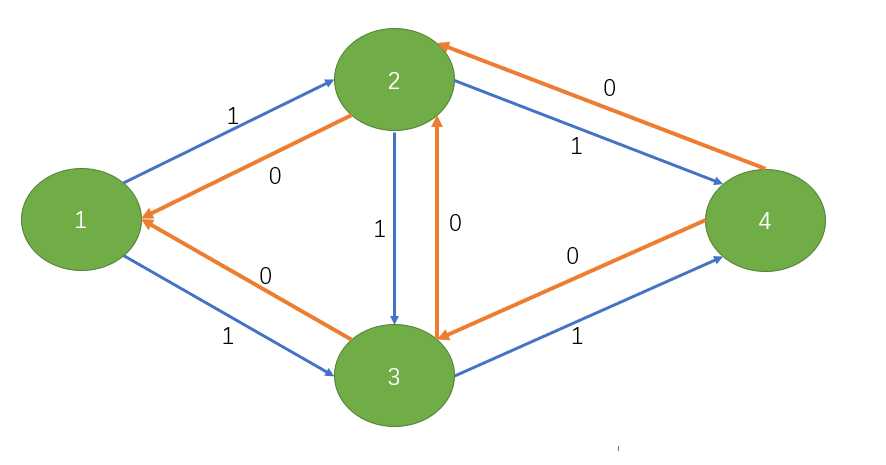
那么对于一条已经增广了的路径来说，我们怎么反悔呢？
当然使给目前弧容量-这条增广路流量，反向弧加上这条增广路流量，这样的话首先这条增广路一定不可能从起点再流过一次一摸一样的了，因为对于任意增广路(S,T)来说，它的最大流量肯定等于这条路所经过的弧(u,v)中c(u,v)最小的那条弧的c(u,v) (好绕口)，所以对于从S到T的某一条增广路来说，这条增广路就可以形成一个"反悔"的模型。
顺便说一句，如果说对于(u,v)来说(v,u)是反向弧的话，那么对于(v,u)来说(u,v)也是反向弧，所以反向弧是相对的
放一组图看一下

对于之前那幅图，我们跑完1->2->3->4这条增广路时整幅图被我们修改成这个样子：

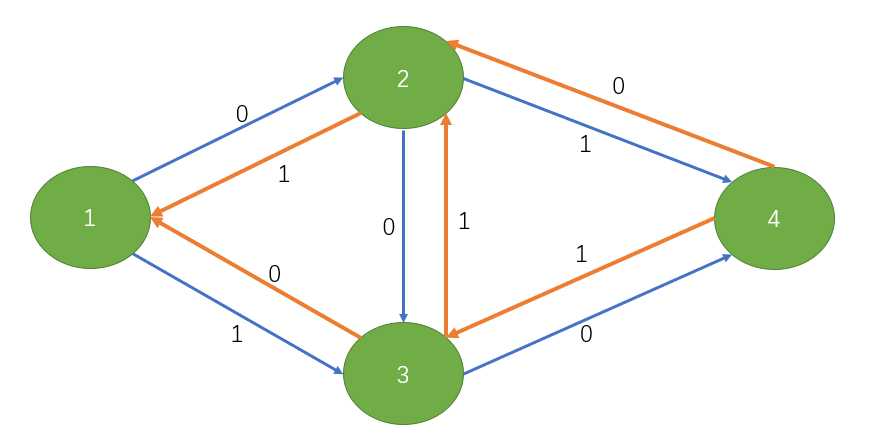
此时，我们还可以走另外一条增广路：1->3->2->4，结果就是这样的：

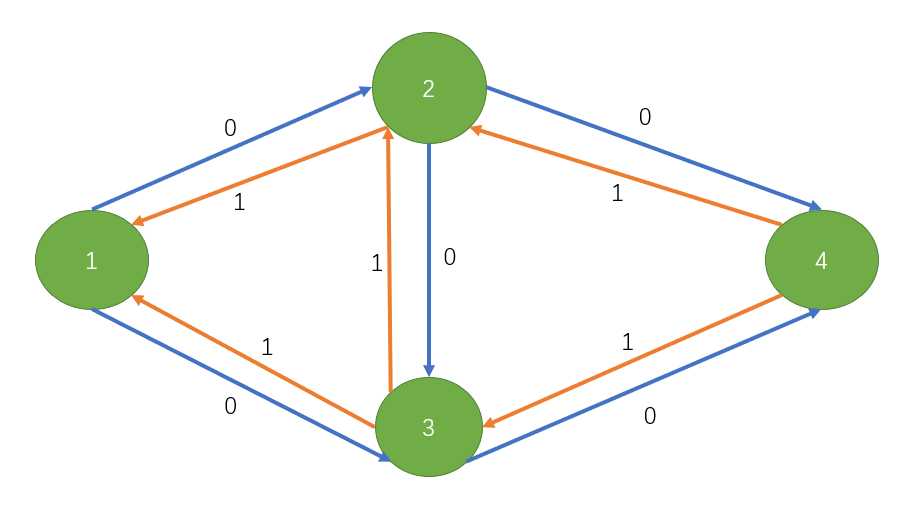
（之前图放错了所以又重新画了一张，有一点不一样应该不影响阅读吧。。。。。。）

此时，我们起点S的出度虽然是2，但是这两条出边的容量都变成0了，所以整个图就跑完了网络流，答案最后算的是2，
这就是著名的Edmond-Karp算法，简称EK算法
所以说dinic呢？？？
不急，我们还没说完。。。
EK算法固然有用，但是它可能会被一些特殊数据卡住：

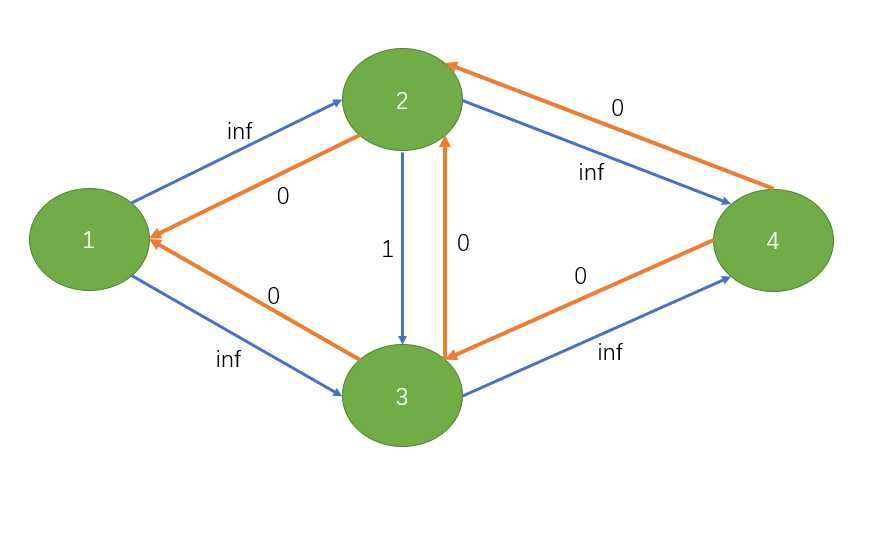
这里的inf只是一个极大值而已 (比如19260817之类的)
那么比如说我们首先增广1->2->3->4这条路径，就会变成这样：

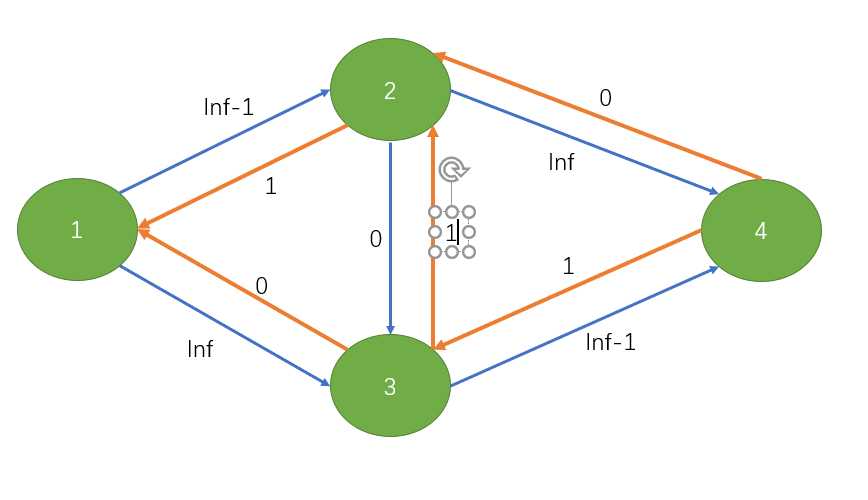
接着我们增广1->3->2->4:

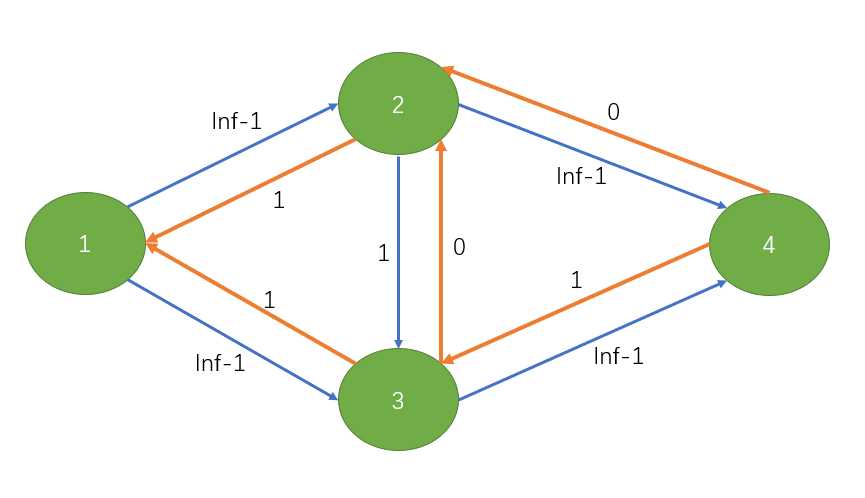
我们会发现，对于这样一个简单的图，我们需要增广2*inf-1次才能完成计算，时间消耗太大，所以我们引入一个方案——给每个点一个“高度”，对于上面的例子，如果我们选择1->2->4或者是1->3->4就不会被卡了，但是我们选择的1->2->3->4，而如果我们通过BFS处理出每个点的“高度”的化，我们会发现你，2和3都是在同一高度的，也就是说弧(2,3)相当于把两条从S到T的最短路给连接起来了。如果我们规定，对于点u,它能增广到的下一个点v必须满足这个条件：depth[v]=dep[u]+1,这样我们就会避免经过某一些同一高度的点，也就是说走的是S到u的最短路。这里说一下，因为网络流里面边的权值是流量而不是长度，所以从S到u的最短路就是u在图里面的深度，可以意会一下。

又到了喜闻乐见的代码时间

首先我们先声明结构体（我比较喜欢的是vector邻接表建图）：

struct edge{
    int to,flow,rev;
    edge(int to_,int flow_,int rev_){
        to=to_;
        flow=flow_;
        rev=rev_;
    }
};
vector<edge> gpe[maxn];

这里的rev有点小trick，我们接下来继续看

为图分层的BFS:

int dep[maxn]；
bool bfs(int st,int ed) {
    memset(dep, 0, sizeof dep);
    queue<int> q;
    q.push(st);
    dep[st] = 1;
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i=0;i<gpe[u].size();i++) {
            int v = gpe[u][i].to;
            if( dep[v] || gpe[u][i].flow <= 0) continue;
            dep[v] = dep[u] + 1;
            q.push(v);
        }
    }
    return dep[ed];
}

也不是很难，唯一要注意的就是要在判断是否取v的时候特殊判一下是否下一条边的容量已经是0了，如狗是0就没办法继续。其他的部分就是一个裸的BFS分层，没什么好讲的

接下来是dfs增广：

int dfs(int u,int flow,int ed){
    if(u == ed) return flow;
    int add = 0;
    for(int i=0;i<gpe[u].size();i++) {
        int v = gpe[u][i].to;
        if(dep[v] != dep[u] + 1) continue;
        if(!gpe[u][i].flow) continue;
        int tmpadd = dfs(v, min(gpe[u][i].flow, flow - add),ed);
        gpe[u][i].flow -= tmpadd;
        gpe[v][gpe[u][i].rev].flow+=tmpadd;
        add += tmpadd;
    }
    return add;
}

最后是dinic函数：

int dinic(int st,int ed){
    int max_flow = 0;
    while (bfs(st,ed)){
        max_flow += dfs(st,inf,ed);
    }
    return max_flow;
}

然后是加边：

void addedge(int u,int v,int w){
    gpe[u].push_back(edge(v,w,gpe[v].size()));
    gpe[v].push_back(edge(u,0,gpe[u].size()-1));
}

这里要看一下，我们反边的意义就是，假如我们现在站在u点，我们指定了g[u][x]这条边进行访问，但是我们同时要得到这个点的反边。虽然我们从u点看是第x条边，但是从v点看却不一定是x,所以这里我们动态计算从v点看的相对位置，具体原理大家可以手动模拟一下 (没有什么问题是手动模拟搞不定的)

总代码（之前那到模板题的代码）：

#include <bits/stdc++.h>
using namespace std;
const int maxn=100010;
const int inf=0x7f;
struct edge{
    int to,flow,rev;
    edge(int to_,int flow_,int rev_){
        to=to_;
        flow=flow_;
        rev=rev_;
    }
};
vector<edge> gpe[maxn];
int dep[maxn];
bool vis[maxn];
bool bfs(int st,int ed) {
    memset(dep, 0, sizeof dep);
    queue<int> q;
    q.push(st);
    dep[st] = 1;
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i=0;i<gpe[u].size();i++) {
            int v = gpe[u][i].to;
            if( dep[v] || gpe[u][i].flow <= 0) continue;
            dep[v] = dep[u] + 1;
            q.push(v);
        }
    }
    return dep[ed];
}
int dfs(int u,int flow,int ed){
    if(u == ed) return flow;
    int add = 0;
    for(int i=0;i<gpe[u].size();i++) {
        int v = gpe[u][i].to;
        if(dep[v] != dep[u] + 1) continue;
        if(!gpe[u][i].flow) continue;
        int tmpadd = dfs(v, min(gpe[u][i].flow, flow - add),ed);
        gpe[u][i].flow -= tmpadd;
        gpe[v][gpe[u][i].rev].flow+=tmpadd;
        add += tmpadd;
    }
    return add;
}
int dinic(int st,int ed){
    int max_flow = 0;
    while (bfs(st,ed)){
        max_flow += dfs(st,inf,ed);
    }
    return max_flow;
}
void addedge(int u,int v,int w){
    gpe[u].push_back(edge(v,w,gpe[v].size()));
    gpe[v].push_back(edge(u,0,gpe[u].size()-1));
}
int main(void){
    int n,m,s,t;
    scanf("%d %d %d %d",&n,&m,&s,&t);
    for(int i=1;i<=m;i++){
        int u,v,w;
        scanf("%d %d %d",&u,&v,&w);
        addedge(u,v,w);
    }
    printf("%d",dinic(s,t));
}

总结

虽然网络流是一个很复杂的东西，但是目前来看在竞赛方面网络流题难点还是建模方面（玄学拆点，玄学连边），并且还有很多的题目表面上看起来和网络流八竿子打不着，但是最终却奇迹般的用网络流解决了。。。 所以做网络流题目一定要有一些经验（一些相关定理）和拆点连边的感觉，仔细分析题意，建模，（然后随便跑一个板子交上去肯定能AC）。