平衡二叉树的旋转类型及代码实现

Posted 2021-03-07 li-ningning

参考了 : http://data.biancheng.net/view/59.html 这篇文章

给大家推荐一个模拟平衡二叉树实现的网站(超级好用): 

 https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

最近花 了点时间 ， 把上课的没明白的平衡二叉树自己又复习了一下，总结一下自己的平衡二叉树；

首先， 对于平衡二叉树 , 要明白是插入了哪个结点,然后破坏了哪个结点的平衡 , 先讲一下旋转类型： 

① ： 最简单的LL型旋转

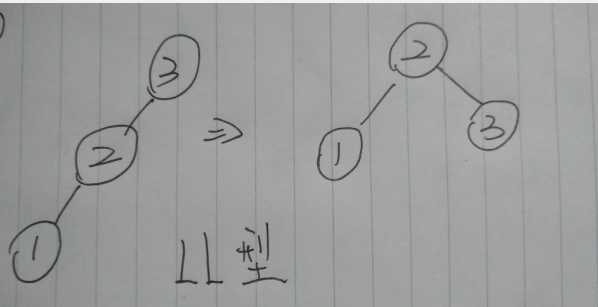
将中间的结点往上移；

② : 最简单的RR型旋转

 

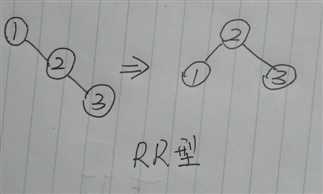
 也是将中间结点上移

③ : LR型 (A类) , 我把LR型旋转的三种情分成了ABC三类

 

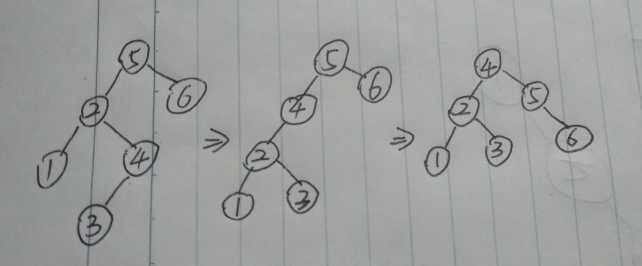
这种LR型（A类）是在插入 3 结点的时候 ， 破坏了 5 结点的平衡 ， 先对 2 结点进行左旋 ，旋转成中间的这种形态 ， 在对 5 结点进行右旋 

 ④ : LR型（B类） 

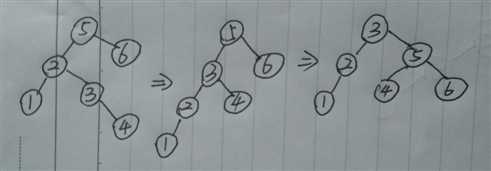
 这种类型的旋转跟上面一种的差不多 , 最主要的就是注意一下 4 这个 结点的情况,最后面是放在了 5 结点的左边

 ⑤ ： LR型（C类）

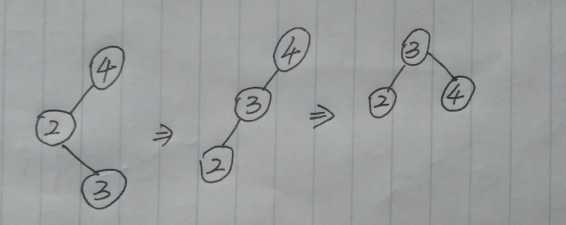
 这类是简单的LR型 ， 失衡点是 4  ， 要先对 2 进行左旋， 调整成中间形态， 再对失衡点 4 进行右旋 

⑥ ： RL型（A类）

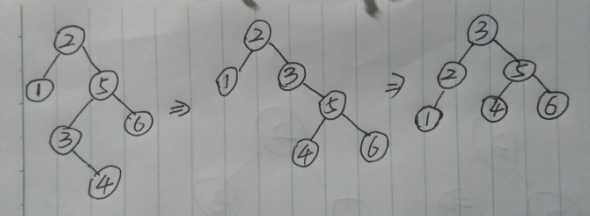
 插入点 4 时 ，失衡点是 2 ， 先对 5 进行右旋 ， 再对 失衡点 2 进行左旋

⑦ ： RL型（B类）

 

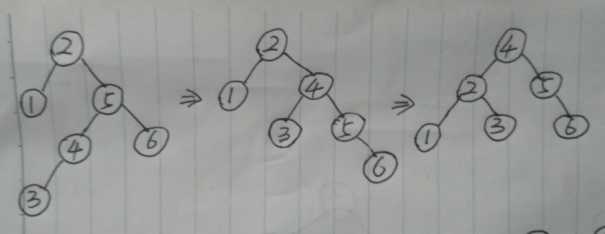
 这个跟RL型（A类）不同的点就是　３　和　４　的位置　

⑧　：RL型（C类）

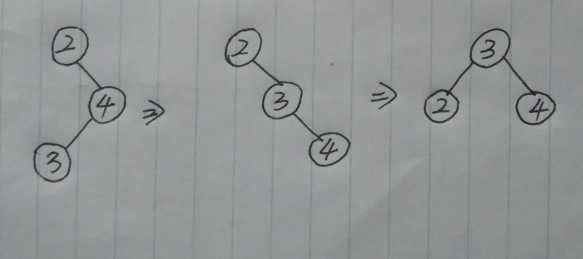
大体可以分成这几种旋转类型 , 把旋转类型理解了 , 就可以看着代码来理解 , 我也是看着代码才弄明白 , 所以不用 慌!

  1 #include<stdlib.h>
  2 #include<stdio.h>
  3 #define EH 0
  4 #define RH -1  /// 这三个是平衡因子
  5 #define LH 1
  6 
  7 typedef struct Node {
  8     int BF ;
  9     int data;
 10     struct Node *left , *right;
 11 }*Bitree , BitreeNode;
 12 
 13 void R_Rotate(Bitree *T)/// 右旋
 14 {
 15     Bitree L = (*T)->left;
 16     (*T)->left = L->right;
 17     L->right = (*T);
 18     *T = L;
 19 }
 20 void L_Rotate(Bitree *T)/// 左旋
 21 {
 22     Bitree L = (*T)->right;
 23     (*T)->right = L->left;
 24     L->left = *T;
 25     *T = L;
 26 }
 27 void LeftBalance(Bitree *T) /// 左边失衡了 , 进行左平衡操作
 28 {
 29     Bitree L , Lr;
 30     L = (*T)->left; /// 失衡点 T 的左孩子进行操作
 31     switch(L->BF){ ///
 32         case LH: /// 左孩子的左边重 , 进行右旋
 33             (*T)->BF = L->BF = EH;///  调节平衡因子在进行旋转
 34             R_Rotate(T); /// 右旋
 35             break;
 36         case RH:///  右边的孩子重 , 这里就是处理 LR 型的开始了, 上面的case是处理LL型的
 37             Lr = L->right; /// 对 L　结点的右孩子进行分析
 38             switch(Lr->BF){
 39                 case EH : /// 右孩子平衡了,其实也就是没有孩子了, 这里处理的就是我们说的 LR型(C类)
 40                     L->BF = EH;
 41                     (*T)->BF = EH;/// 先将平衡因子进行修改, 后面在进行旋转
 42                     break;
 43                 case RH: /// 有一个右孩子, 这里就是 LR型(B类)的处理
 44                     L->BF = LH;
 45                     (*T)->BF = EH;
 46                     break;
 47                 case LH: /// LR型(A类)的处理
 48                     L->BF = EH;
 49                     (*T)->BF = RH;
 50                     break;
 51             }
 52         Lr->BF = EH; /// 修改平衡因子 , 然后进行 LR旋转
 53         L_Rotate(&(*T)->left);/// 先对子树进行左旋，这里要写成(*T)->left的，不能写 &L 的，
 54         ///虽然L指向(*T)的左孩子 ， 但是地址不一样！不能混
 55 
 56         R_Rotate(T);///  在对失衡点(*T)进行右旋
 57         break;
 58     }
 59 }
 60 ///下面是 右边失去平衡的调整操作 ，跟上面的是一个原理，可以对着图片的旋转来看
 61 void RightBalance(Bitree *T)
 62 {
 63     Bitree L , Lr;
 64     Lr = (*T)->right;
 65     switch(Lr->BF){
 66         case RH :
 67             Lr->BF = EH;
 68             (*T)->BF = EH;
 69             L_Rotate(T);
 70             break;
 71         case LH:
 72             L = Lr->left ;
 73             switch(L->BF){
 74                 case LH:
 75                     (*T)->BF = EH;
 76                     Lr->BF = RH;
 77                     break;
 78                 case RH :///
 79                     (*T)->BF = LH;
 80                     Lr->BF = EH;
 81                     break;
 82                 case EH:
 83                     Lr->BF = EH;
 84                     (*T)->BF = EH;
 85                     break;
 86             }
 87         L->BF = EH;
 88         R_Rotate(&(*T)->right);
 89         L_Rotate(T);
 90         break;
 91     }
 92 }
 93 int Insert(Bitree *T , int data , bool *taller)/// 插入操作
 94 {
 95 
 96     if((*T)==NULL){ /// 树空 , 添加结点
 97         (*T) = (Bitree)malloc(sizeof(BitreeNode));
 98         (*T)->BF = EH;
 99         (*T)->data = data;
100         (*T)->left = NULL;
101         (*T)->right = NULL;
102         *taller = true;
103     }
104     else if(data == (*T)->data){/// 树中有这个数据点了
105         *taller = false;/// 没有插入数据
106         return 0;///  插入失败 ， 返回0
107     }
108     else if (data < (*T)->data){
109         if( !Insert(&(*T)->left , data , taller)) /// 判断插入是否成功
110             return 0;
111         if(*taller)
112         switch((*T)->BF){/// 根据 平衡因子判断插入方向以及是否要旋转等
113             case LH:
114                 LeftBalance(T); /// 插入的话 ， 就变成了 LL型 或 LR型 ， 所以进行左边平衡操作
115                 *taller = false;
116                 break;
117             case EH :/// 这种的话，平衡没有破坏，就调一下平衡因子就行了
118                 (*T)->BF =LH;
119                 *taller = true;
120                 break;
121             case RH:
122                 (*T)->BF = EH;
123                 *taller = false;
124                 break;
125 
126         }
127     }
128     else{///原理同上
129         if( !Insert(&(*T)->right , data , taller))
130             return 0;
131         if(*taller)
132         switch((*T)->BF){
133             case LH:
134                 (*T)->BF = EH;
135                 *taller = false;
136                 break;
137             case EH:
138                 (*T)->BF = RH;
139                 *taller = true;
140                 break;
141             case RH:
142                 RightBalance(T);
143                 *taller = false;
144                 break;
145         }
146     }
147     return 1;
148 }
149 void traverse(Bitree T)
150 {
151 
152     if(T){
153         printf("%d " , T->data);
154         traverse(T->left);
155         traverse(T->right);
156     }
157 }
158 int main()
159 {
160     int a ;
161     Bitree T = NULL;
162     bool taller = false;
163     while(~scanf("%d",&a))
164         Insert(&T , a , &taller);
165     traverse(T);
166     return 0;
167 }

大概就是这样子了.