平衡二叉树的旋转

Posted 2021-04-09 宏睿技术

一、平衡二叉树的定义

    为避免树的高度增长过快，降低二叉树的排序性能，规定在插入和删除二叉树结点时，保证任意结点的左右子树高度差的绝对值不大于1。这样的二叉树被称为平衡二叉树（Balanced Binary Tree）。

二、平衡因子

    平衡因子：结点的平衡因子 = 结点的左子树深度 — 结点的右子树深度。若平衡因子的取值为-1、0或1时，该节点是平衡的，否则是不平衡的。

最低不平衡结点：用A表示最低不平衡结点，则A的祖先结点可能有不平衡的，但其所有后代结点都是平衡的。

简单理解为：一个结点的左右子树高度差不超过一，超过一就不平衡，需要进行旋转。

二、LL平衡旋转（右单旋转）

    B→根节点，B的右子树成为A的左子树

实现代码：

void rRotate(Node *Parent)//LL { Node *subL = Parent->_pLeft; Node *subLR = subL->_pRight; Parent->_pLeft = subLR; if (subLR)//左单支 subLR->_parent = Parent; subL->_pRight = Parent; Node *pParent = Parent->_parent; Parent->_parent = subL; subL->_parent = pParent; if (NULL == pParent)//Parent是根节点 _pRoot = subL; else if (Parent == pParent->_pLeft) pParent->_pLeft = subL; else pParent->_pRight = subL; //修改平衡因子 subL->_bf = 0; Parent->_bf = 0; }

    三、RR旋转（左单旋转）B左上为根，B的左子树成为A的右子树

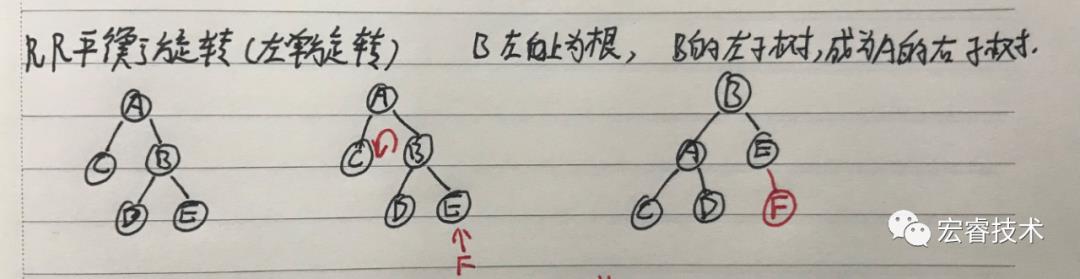
实现代码：

void lRotate(Node *Parent)//RR { Node *subR = Parent->_pRight; Node *subRL = subR->_pLeft; Parent->_pRight = subRL; if (subRL) subRL->_parent = Parent; subR->_pLeft = Parent; subR->_parent = Parent->_parent; Parent->_parent = subR; Node *pParent = subR->_parent; if (NULL == pParent) _pRoot = subR; else if (Parent == pParent->_pLeft) pParent->_pLeft = subR; else pParent->_pRight = subR; Parent->_bf = 0; subR->_bf = 0; }

四、LR平衡双旋转（先左后右双旋转）由基础旋转组合而来

实现代码：

void lrRotate(Node *Parent)//LR { Node *subL = Parent->_pLeft; Node *subLR = subL->_pRight; int bf = subLR->_bf; lRotate(Parent->_pLeft); rRotate(Parent); if (1 == bf) subL->_bf = -1; else if (-1 == bf) Parent->_bf = 1; subLR->_bf = 0; }

五、RL平衡旋转（先右后左双旋转）组合旋转，可以分为两步进行旋转

实现代码：

void rlRotate(Node *Parent) { Node *subR = Parent->_pRight; Node *subRL = subR->_pLeft; int bf = subRL->_bf; rRotate(Parent->_pRight); lRotate(Parent); if (1 == bf) Parent->_bf = -1; else if (-1 == bf) subR->_bf = 1; subRL->_bf = 0; }

AVL树插入代码：

bool Insert(const K& key, const V& value) { Node *pNew = new Node(key,value); Node *pCur = _pRoot; Node *parent = NULL; if (NULL == _pRoot) { _pRoot = pNew; return true; } while (pCur)//寻找插入位置 { if (key < pCur->_key) { parent = pCur; pCur = pCur->_pLeft; } else if (key > pCur->_key) { parent = pCur; pCur = pCur->_pRight; } else return false; } if (key < parent->_key)//插入元素 parent->_pLeft = pNew; else parent->_pRight = pNew; pNew->_parent = parent; //修改平衡因子 while (parent) { if (pNew == parent->_pLeft) parent->_bf--; else parent->_bf++; if (0 == parent->_bf) return true; else if (1 == parent->_bf || -1 == parent->_bf) { pNew = parent; parent = parent->_parent; } else//2需要进行旋转 { if (-2 == parent->_bf && -1 == pNew->_bf)//LL rRotate(parent); else if (2 == parent->_bf && 1 == pNew->_bf)//RR lRotate(parent); else if (-2 == parent->_bf && 1 == pNew->_bf)//LR lrRotate(parent); else if (2 == parent->_bf && -1 == pNew->_bf)//RL rlRotate(parent); return true; } } return true; }

本文参考算法网平衡二叉树旋转详解，和王道论坛。