玩转数据结构：第7章 集合和映射

Posted 2021-03-07 marlonkang

7-1 集合基础和基于二分搜索树的集合实现

07-Set-and-Map

集合

01-Set-Basics-and-BSTSet

 

文件IO操作，简单分词工具类

FileOperation

import java.io.FileInputStream;
import java.util.ArrayList;
import java.util.Scanner;
import java.util.Locale;
import java.io.File;
import java.io.BufferedInputStream;
import java.io.IOException;

// 文件相关操作
public class FileOperation {

    // 读取文件名称为filename中的内容，并将其中包含的所有词语放进words中
    public static boolean readFile(String filename, ArrayList<String> words){

        if (filename == null || words == null){
            System.out.println("filename is null or words is null");
            return false;
        }

        // 文件读取
        Scanner scanner;

        try {
            File file = new File(filename);
            if(file.exists()){
                FileInputStream fis = new FileInputStream(file);
                scanner = new Scanner(new BufferedInputStream(fis), "UTF-8");
                scanner.useLocale(Locale.ENGLISH);
            }
            else
                return false;
        }
        catch(IOException ioe){
            System.out.println("Cannot open " + filename);
            return false;
        }

        // 简单分词
        // 这个分词方式相对简陋, 没有考虑很多文本处理中的特殊问题
        // 在这里只做demo展示用
        if (scanner.hasNextLine()) {

            String contents = scanner.useDelimiter("A").next();

            int start = firstCharacterIndex(contents, 0);
            for (int i = start + 1; i <= contents.length(); )
                if (i == contents.length() || !Character.isLetter(contents.charAt(i))) {
                    String word = contents.substring(start, i).toLowerCase();
                    words.add(word);
                    start = firstCharacterIndex(contents, i);
                    i = start + 1;
                } else
                    i++;
        }

        return true;
    }

    // 寻找字符串s中，从start的位置开始的第一个字母字符的位置
    private static int firstCharacterIndex(String s, int start){

        for( int i = start ; i < s.length() ; i ++ )
            if( Character.isLetter(s.charAt(i)) )
                return i;
        return s.length();
    }
}

View Code

二分搜索树底层实现

BST.java

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class BST<E extends Comparable<E>> {

    private class Node{
        public E e;
        public Node left, right;

        public Node(E e){
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){

        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){

        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    // 二分搜索树的非递归前序遍历
    public void preOrderNR(){

        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            Node cur = stack.pop();
            System.out.println(cur.e);

            if(cur.right != null)
                stack.push(cur.right);
            if(cur.left != null)
                stack.push(cur.left);
        }
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node){

        if(node == null)
            return;

        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    // 后序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node){

        if(node == null)
            return;

        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

    // 二分搜索树的层序遍历
    public void levelOrder(){

        Queue<Node> q = new LinkedList<>();
        q.add(root);
        while(!q.isEmpty()){
            Node cur = q.remove();
            System.out.println(cur.e);

            if(cur.left != null)
                q.add(cur.left);
            if(cur.right != null)
                q.add(cur.right);
        }
    }

    // 寻找二分搜索树的最小元素
    public E minimum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty!");

        return minimum(root).e;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null)
            return node;
        return minimum(node.left);
    }

    // 寻找二分搜索树的最大元素
    public E maximum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty");

        return maximum(root).e;
    }

    // 返回以node为根的二分搜索树的最大值所在的节点
    private Node maximum(Node node){
        if(node.right == null)
            return node;

        return maximum(node.right);
    }

    // 从二分搜索树中删除最小值所在节点, 返回最小值
    public E removeMin(){
        E ret = minimum();
        root = removeMin(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){

        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }

    // 从二分搜索树中删除最大值所在节点
    public E removeMax(){
        E ret = maximum();
        root = removeMax(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMax(Node node){

        if(node.right == null){
            Node leftNode = node.left;
            node.left = null;
            size --;
            return leftNode;
        }

        node.right = removeMax(node.right);
        return node;
    }

    // 从二分搜索树中删除元素为e的节点
    public void remove(E e){
        root = remove(root, e);
    }

    // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    private Node remove(Node node, E e){

        if( node == null )
            return null;

        if( e.compareTo(node.e) < 0 ){
            node.left = remove(node.left , e);
            return node;
        }
        else if(e.compareTo(node.e) > 0 ){
            node.right = remove(node.right, e);
            return node;
        }
        else{   // e.compareTo(node.e) == 0

            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }

            // 待删除节点右子树为空的情况
            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }

            // 待删除节点左右子树均不为空的情况

            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;

            node.left = node.right = null;

            return successor;
        }
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null
");
            return;
        }

        res.append(generateDepthString(depth) + node.e +"
");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}

View Code

Set集合接口

public interface Set<E> {

    void add(E e);
    boolean contains(E e);
    void remove(E e);
    int getSize();
    boolean isEmpty();
}

View Code

BSTSet集合实现类

public class BSTSet<E extends Comparable<E>> implements Set<E> {

    private BST<E> bst;

    public BSTSet(){
        bst = new BST<>();
    }

    @Override
    public int getSize(){
        return bst.size();
    }

    @Override
    public boolean isEmpty(){
        return bst.isEmpty();
    }

    @Override
    public void add(E e){
        bst.add(e);
    }

    @Override
    public boolean contains(E e){
        return bst.contains(e);
    }

    @Override
    public void remove(E e){
        bst.remove(e);
    }
}

View Code

测试主程序入口

Main.java

import java.util.ArrayList;

public class Main {

    public static void main(String[] args) {

        System.out.println("Pride and Prejudice");

        ArrayList<String> words1 = new ArrayList<>();
        if(FileOperation.readFile("pride-and-prejudice.txt", words1)) {
            System.out.println("Total words: " + words1.size());

            BSTSet<String> set1 = new BSTSet<>();
            for (String word : words1)
                set1.add(word);
            System.out.println("Total different words: " + set1.getSize());
        }

        System.out.println();


        System.out.println("A Tale of Two Cities");

        ArrayList<String> words2 = new ArrayList<>();
        if(FileOperation.readFile("a-tale-of-two-cities.txt", words2)){
            System.out.println("Total words: " + words2.size());

            BSTSet<String> set2 = new BSTSet<>();
            for(String word: words2)
                set2.add(word);
            System.out.println("Total different words: " + set2.getSize());
        }
    }
}

View Code

a-tale-of-two-cities.txt

pride-and-prejudice.txt

 

7-2 基于链表的集合实现

02-LinkedListSet 

Set集合接口

public interface Set<E> {

    void add(E e);
    boolean contains(E e);
    void remove(E e);
    int getSize();
    boolean isEmpty();
}

View Code

动态数据结构的底层实现

LinkedList

public class LinkedList<E> {

    private class Node{
        public E e;
        public Node next;

        public Node(E e, Node next){
            this.e = e;
            this.next = next;
        }

        public Node(E e){
            this(e, null);
        }

        public Node(){
            this(null, null);
        }

        @Override
        public String toString(){
            return e.toString();
        }
    }

    private Node dummyHead;
    private int size;

    public LinkedList(){
        dummyHead = new Node();
        size = 0;
    }

    // 获取链表中的元素个数
    public int getSize(){
        return size;
    }

    // 返回链表是否为空
    public boolean isEmpty(){
        return size == 0;
    }

    // 在链表的index(0-based)位置添加新的元素e
    // 在链表中不是一个常用的操作，练习用：）
    public void add(int index, E e){

        if(index < 0 || index > size)
            throw new IllegalArgumentException("Add failed. Illegal index.");

        Node prev = dummyHead;
        for(int i = 0 ; i < index ; i ++)
            prev = prev.next;

        prev.next = new Node(e, prev.next);
        size ++;
    }

    // 在链表头添加新的元素e
    public void addFirst(E e){
        add(0, e);
    }

    // 在链表末尾添加新的元素e
    public void addLast(E e){
        add(size, e);
    }

    // 获得链表的第index(0-based)个位置的元素
    // 在链表中不是一个常用的操作，练习用：）
    public E get(int index){

        if(index < 0 || index >= size)
            throw new IllegalArgumentException("Get failed. Illegal index.");

        Node cur = dummyHead.next;
        for(int i = 0 ; i < index ; i ++)
            cur = cur.next;
        return cur.e;
    }

    // 获得链表的第一个元素
    public E getFirst(){
        return get(0);
    }

    // 获得链表的最后一个元素
    public E getLast(){
        return get(size - 1);
    }

    // 修改链表的第index(0-based)个位置的元素为e
    // 在链表中不是一个常用的操作，练习用：）
    public void set(int index, E e){
        if(index < 0 || index >= size)
            throw new IllegalArgumentException("Set failed. Illegal index.");

        Node cur = dummyHead.next;
        for(int i = 0 ; i < index ; i ++)
            cur = cur.next;
        cur.e = e;
    }

    // 查找链表中是否有元素e
    public boolean contains(E e){
        Node cur = dummyHead.next;
        while(cur != null){
            if(cur.e.equals(e))
                return true;
            cur = cur.next;
        }
        return false;
    }

    // 从链表中删除index(0-based)位置的元素, 返回删除的元素
    // 在链表中不是一个常用的操作，练习用：）
    public E remove(int index){
        if(index < 0 || index >= size)
            throw new IllegalArgumentException("Remove failed. Index is illegal.");

        Node prev = dummyHead;
        for(int i = 0 ; i < index ; i ++)
            prev = prev.next;

        Node retNode = prev.next;
        prev.next = retNode.next;
        retNode.next = null;
        size --;

        return retNode.e;
    }

    // 从链表中删除第一个元素, 返回删除的元素
    public E removeFirst(){
        return remove(0);
    }

    // 从链表中删除最后一个元素, 返回删除的元素
    public E removeLast(){
        return remove(size - 1);
    }

    // 从链表中删除元素e
    public void removeElement(E e){

        Node prev = dummyHead;
        while(prev.next != null){
            if(prev.next.e.equals(e))
                break;
            prev = prev.next;
        }

        if(prev.next != null){
            Node delNode = prev.next;
            prev.next = delNode.next;
            delNode.next = null;
            size --;
        }
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();

        Node cur = dummyHead.next;
        while(cur != null){
            res.append(cur + "->");
            cur = cur.next;
        }
        res.append("NULL");

        return res.toString();
    }
}

View Code

集合接口的实现类

LinkedListSet

import java.util.ArrayList;

public class LinkedListSet<E> implements Set<E> {

    private LinkedList<E> list;

    public LinkedListSet(){
        list = new LinkedList<>();
    }

    @Override
    public int getSize(){
        return list.getSize();
    }

    @Override
    public boolean isEmpty(){
        return list.isEmpty();
    }

    @Override
    public void add(E e){
        if(!list.contains(e))
            list.addFirst(e);
    }

    @Override
    public boolean contains(E e){
        return list.contains(e);
    }

    @Override
    public void remove(E e){
        list.removeElement(e);
    }

    public static void main(String[] args) {

        System.out.println("Pride and Prejudice");

        ArrayList<String> words1 = new ArrayList<>();
        if(FileOperation.readFile("pride-and-prejudice.txt", words1)) {
            System.out.println("Total words: " + words1.size());

            LinkedListSet<String> set1 = new LinkedListSet<>();
            for (String word : words1)
                set1.add(word);
            System.out.println("Total different words: " + set1.getSize());
        }

        System.out.println();


        System.out.println("A Tale of Two Cities");

        ArrayList<String> words2 = new ArrayList<>();
        if(FileOperation.readFile("a-tale-of-two-cities.txt", words2)){
            System.out.println("Total words: " + words2.size());

            LinkedListSet<String> set2 = new LinkedListSet<>();
            for(String word: words2)
                set2.add(word);
            System.out.println("Total different words: " + set2.getSize());
        }
    }
}

View Code

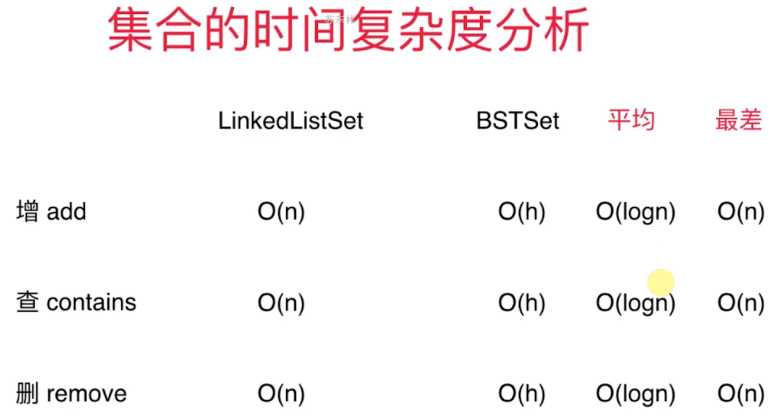
7-3 集合类的复杂度分析

03-Time-Complexity-of-Set

Main

import java.util.ArrayList;

public class Main {

    private static double testSet(Set<String> set, String filename){

        long startTime = System.nanoTime();

        System.out.println(filename);
        ArrayList<String> words = new ArrayList<>();
        if(FileOperation.readFile(filename, words)) {
            System.out.println("Total words: " + words.size());

            for (String word : words)
                set.add(word);
            System.out.println("Total different words: " + set.getSize());
        }
        long endTime = System.nanoTime();

        return (endTime - startTime) / 1000000000.0;
    }

    public static void main(String[] args) {

        String filename = "pride-and-prejudice.txt";

        BSTSet<String> bstSet = new BSTSet<>();
        double time1 = testSet(bstSet, filename);
        System.out.println("BST Set: " + time1 + " s");

        System.out.println();

        LinkedListSet<String> linkedListSet = new LinkedListSet<>();
        double time2 = testSet(linkedListSet, filename);
        System.out.println("Linked List Set: " + time2 + " s");

    }
}

View Code

7-4 Leetcode中的集合问题和更多集合相关问题

04-TreeSet-and-Set-Problems-in-Leetcode

// Leetcode 804. Unique Morse Code Words
// https://leetcode.com/problems/unique-morse-code-words/description/

LinkedListSetSolution

// Leetcode 804. Unique Morse Code Words
// https://leetcode.com/problems/unique-morse-code-words/description/

public class LinkedListSetSolution {

    private class LinkedList<E> {

        private class Node{
            public E e;
            public Node next;

            public Node(E e, Node next){
                this.e = e;
                this.next = next;
            }

            public Node(E e){
                this(e, null);
            }

            public Node(){
                this(null, null);
            }

            @Override
            public String toString(){
                return e.toString();
            }
        }

        private Node dummyHead;
        private int size;

        public LinkedList(){
            dummyHead = new Node();
            size = 0;
        }

        // 获取链表中的元素个数
        public int getSize(){
            return size;
        }

        // 返回链表是否为空
        public boolean isEmpty(){
            return size == 0;
        }

        // 在链表的index(0-based)位置添加新的元素e
        // 在链表中不是一个常用的操作，练习用：）
        public void add(int index, E e){

            if(index < 0 || index > size)
                throw new IllegalArgumentException("Add failed. Illegal index.");

            Node prev = dummyHead;
            for(int i = 0 ; i < index ; i ++)
                prev = prev.next;

            prev.next = new Node(e, prev.next);
            size ++;
        }

        // 在链表头添加新的元素e
        public void addFirst(E e){
            add(0, e);
        }

        // 在链表末尾添加新的元素e
        public void addLast(E e){
            add(size, e);
        }

        // 获得链表的第index(0-based)个位置的元素
        // 在链表中不是一个常用的操作，练习用：）
        public E get(int index){

            if(index < 0 || index >= size)
                throw new IllegalArgumentException("Get failed. Illegal index.");

            Node cur = dummyHead.next;
            for(int i = 0 ; i < index ; i ++)
                cur = cur.next;
            return cur.e;
        }

        // 获得链表的第一个元素
        public E getFirst(){
            return get(0);
        }

        // 获得链表的最后一个元素
        public E getLast(){
            return get(size - 1);
        }

        // 修改链表的第index(0-based)个位置的元素为e
        // 在链表中不是一个常用的操作，练习用：）
        public void set(int index, E e){
            if(index < 0 || index >= size)
                throw new IllegalArgumentException("Set failed. Illegal index.");

            Node cur = dummyHead.next;
            for(int i = 0 ; i < index ; i ++)
                cur = cur.next;
            cur.e = e;
        }

        // 查找链表中是否有元素e
        public boolean contains(E e){
            Node cur = dummyHead.next;
            while(cur != null){
                if(cur.e.equals(e))
                    return true;
                cur = cur.next;
            }
            return false;
        }

        // 从链表中删除index(0-based)位置的元素, 返回删除的元素
        // 在链表中不是一个常用的操作，练习用：）
        public E remove(int index){
            if(index < 0 || index >= size)
                throw new IllegalArgumentException("Remove failed. Index is illegal.");

            Node prev = dummyHead;
            for(int i = 0 ; i < index ; i ++)
                prev = prev.next;

            Node retNode = prev.next;
            prev.next = retNode.next;
            retNode.next = null;
            size --;

            return retNode.e;
        }

        // 从链表中删除第一个元素, 返回删除的元素
        public E removeFirst(){
            return remove(0);
        }

        // 从链表中删除最后一个元素, 返回删除的元素
        public E removeLast(){
            return remove(size - 1);
        }

        // 从链表中删除元素e
        public void removeElement(E e){

            Node prev = dummyHead;
            while(prev.next != null){
                if(prev.next.e.equals(e))
                    break;
                prev = prev.next;
            }

            if(prev.next != null){
                Node delNode = prev.next;
                prev.next = delNode.next;
                delNode.next = null;
                size --;
            }
        }

        @Override
        public String toString(){
            StringBuilder res = new StringBuilder();

            Node cur = dummyHead.next;
            while(cur != null){
                res.append(cur + "->");
                cur = cur.next;
            }
            res.append("NULL");

            return res.toString();
        }
    }

    private interface Set<E> {

        void add(E e);
        boolean contains(E e);
        void remove(E e);
        int getSize();
        boolean isEmpty();
    }

    private class LinkedListSet<E> implements Set<E> {

        private LinkedList<E> list;

        public LinkedListSet(){
            list = new LinkedList<>();
        }

        @Override
        public int getSize(){
            return list.getSize();
        }

        @Override
        public boolean isEmpty(){
            return list.isEmpty();
        }

        @Override
        public void add(E e){
            if(!list.contains(e))
                list.addFirst(e);
        }

        @Override
        public boolean contains(E e){
            return list.contains(e);
        }

        @Override
        public void remove(E e){
            list.removeElement(e);
        }
    }

    public int uniqueMorseRepresentations(String[] words) {

        String[] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
        LinkedListSet<String> set = new LinkedListSet<>();
        for(String word: words){
            StringBuilder res = new StringBuilder();
            for(int i = 0 ; i < word.length() ; i ++)
                res.append(codes[word.charAt(i) - ‘a‘]);

            set.add(res.toString());
        }

        return set.getSize();
    }
}

View Code

BSTSetSolution

// Leetcode 804. Unique Morse Code Words
// https://leetcode.com/problems/unique-morse-code-words/description/

import java.util.Stack;
import java.util.Queue;
import java.util.LinkedList;

public class BSTSetSolution {

    private class BST<E extends Comparable<E>> {

        private class Node{
            public E e;
            public Node left, right;

            public Node(E e){
                this.e = e;
                left = null;
                right = null;
            }
        }

        private Node root;
        private int size;

        public BST(){
            root = null;
            size = 0;
        }

        public int size(){
            return size;
        }

        public boolean isEmpty(){
            return size == 0;
        }

        // 向二分搜索树中添加新的元素e
        public void add(E e){
            root = add(root, e);
        }

        // 向以node为根的二分搜索树中插入元素e，递归算法
        // 返回插入新节点后二分搜索树的根
        private Node add(Node node, E e){

            if(node == null){
                size ++;
                return new Node(e);
            }

            if(e.compareTo(node.e) < 0)
                node.left = add(node.left, e);
            else if(e.compareTo(node.e) > 0)
                node.right = add(node.right, e);

            return node;
        }

        // 看二分搜索树中是否包含元素e
        public boolean contains(E e){
            return contains(root, e);
        }

        // 看以node为根的二分搜索树中是否包含元素e, 递归算法
        private boolean contains(Node node, E e){

            if(node == null)
                return false;

            if(e.compareTo(node.e) == 0)
                return true;
            else if(e.compareTo(node.e) < 0)
                return contains(node.left, e);
            else // e.compareTo(node.e) > 0
                return contains(node.right, e);
        }

        // 二分搜索树的前序遍历
        public void preOrder(){
            preOrder(root);
        }

        // 前序遍历以node为根的二分搜索树, 递归算法
        private void preOrder(Node node){

            if(node == null)
                return;

            System.out.println(node.e);
            preOrder(node.left);
            preOrder(node.right);
        }

        // 二分搜索树的非递归前序遍历
        public void preOrderNR(){

            Stack<Node> stack = new Stack<>();
            stack.push(root);
            while(!stack.isEmpty()){
                Node cur = stack.pop();
                System.out.println(cur.e);

                if(cur.right != null)
                    stack.push(cur.right);
                if(cur.left != null)
                    stack.push(cur.left);
            }
        }

        // 二分搜索树的中序遍历
        public void inOrder(){
            inOrder(root);
        }

        // 中序遍历以node为根的二分搜索树, 递归算法
        private void inOrder(Node node){

            if(node == null)
                return;

            inOrder(node.left);
            System.out.println(node.e);
            inOrder(node.right);
        }

        // 二分搜索树的后序遍历
        public void postOrder(){
            postOrder(root);
        }

        // 后序遍历以node为根的二分搜索树, 递归算法
        private void postOrder(Node node){

            if(node == null)
                return;

            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.e);
        }

        // 二分搜索树的层序遍历
        public void levelOrder(){

            Queue<Node> q = new LinkedList<>();
            q.add(root);
            while(!q.isEmpty()){
                Node cur = q.remove();
                System.out.println(cur.e);

                if(cur.left != null)
                    q.add(cur.left);
                if(cur.right != null)
                    q.add(cur.right);
            }
        }

        // 寻找二分搜索树的最小元素
        public E minimum(){
            if(size == 0)
                throw new IllegalArgumentException("BST is empty!");

            return minimum(root).e;
        }

        // 返回以node为根的二分搜索树的最小值所在的节点
        private Node minimum(Node node){
            if(node.left == null)
                return node;
            return minimum(node.left);
        }

        // 寻找二分搜索树的最大元素
        public E maximum(){
            if(size == 0)
                throw new IllegalArgumentException("BST is empty");

            return maximum(root).e;
        }

        // 返回以node为根的二分搜索树的最大值所在的节点
        private Node maximum(Node node){
            if(node.right == null)
                return node;

            return maximum(node.right);
        }

        // 从二分搜索树中删除最小值所在节点, 返回最小值
        public E removeMin(){
            E ret = minimum();
            root = removeMin(root);
            return ret;
        }

        // 删除掉以node为根的二分搜索树中的最小节点
        // 返回删除节点后新的二分搜索树的根
        private Node removeMin(Node node){

            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }

            node.left = removeMin(node.left);
            return node;
        }

        // 从二分搜索树中删除最大值所在节点
        public E removeMax(){
            E ret = maximum();
            root = removeMax(root);
            return ret;
        }

        // 删除掉以node为根的二分搜索树中的最大节点
        // 返回删除节点后新的二分搜索树的根
        private Node removeMax(Node node){

            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }

            node.right = removeMax(node.right);
            return node;
        }

        // 从二分搜索树中删除元素为e的节点
        public void remove(E e){
            root = remove(root, e);
        }

        // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
        // 返回删除节点后新的二分搜索树的根
        private Node remove(Node node, E e){

            if( node == null )
                return null;

            if( e.compareTo(node.e) < 0 ){
                node.left = remove(node.left , e);
                return node;
            }
            else if(e.compareTo(node.e) > 0 ){
                node.right = remove(node.right, e);
                return node;
            }
            else{   // e.compareTo(node.e) == 0

                // 待删除节点左子树为空的情况
                if(node.left == null){
                    Node rightNode = node.right;
                    node.right = null;
                    size --;
                    return rightNode;
                }

                // 待删除节点右子树为空的情况
                if(node.right == null){
                    Node leftNode = node.left;
                    node.left = null;
                    size --;
                    return leftNode;
                }

                // 待删除节点左右子树均不为空的情况

                // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
                // 用这个节点顶替待删除节点的位置
                Node successor = minimum(node.right);
                successor.right = removeMin(node.right);
                successor.left = node.left;

                node.left = node.right = null;

                return successor;
            }
        }

        @Override
        public String toString(){
            StringBuilder res = new StringBuilder();
            generateBSTString(root, 0, res);
            return res.toString();
        }

        // 生成以node为根节点，深度为depth的描述二叉树的字符串
        private void generateBSTString(Node node, int depth, StringBuilder res){

            if(node == null){
                res.append(generateDepthString(depth) + "null
");
                return;
            }

            res.append(generateDepthString(depth) + node.e +"
");
            generateBSTString(node.left, depth + 1, res);
            generateBSTString(node.right, depth + 1, res);
        }

        private String generateDepthString(int depth){
            StringBuilder res = new StringBuilder();
            for(int i = 0 ; i < depth ; i ++)
                res.append("--");
            return res.toString();
        }
    }

    private interface Set<E> {

        void add(E e);
        boolean contains(E e);
        void remove(E e);
        int getSize();
        boolean isEmpty();
    }

    private class BSTSet<E extends Comparable<E>> implements Set<E> {

        private BST<E> bst;

        public BSTSet(){
            bst = new BST<>();
        }

        @Override
        public int getSize(){
            return bst.size();
        }

        @Override
        public boolean isEmpty(){
            return bst.isEmpty();
        }

        @Override
        public void add(E e){
            bst.add(e);
        }

        @Override
        public boolean contains(E e){
            return bst.contains(e);
        }

        @Override
        public void remove(E e){
            bst.remove(e);
        }
    }

    public int uniqueMorseRepresentations(String[] words) {

        String[] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
        BSTSet<String> set = new BSTSet<>();
        for(String word: words){
            StringBuilder res = new StringBuilder();
            for(int i = 0 ; i < word.length() ; i ++)
                res.append(codes[word.charAt(i) - ‘a‘]);

            set.add(res.toString());
        }

        return set.getSize();
    }
}

View Code

底层是平衡二叉树（红黑树）

Solution.java

// Leetcode 804. Unique Morse Code Words
// https://leetcode.com/problems/unique-morse-code-words/description/

import java.util.TreeSet;

public class Solution {

    public int uniqueMorseRepresentations(String[] words) {

        String[] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
        TreeSet<String> set = new TreeSet<>();
        for(String word: words){
            StringBuilder res = new StringBuilder();
            for(int i = 0 ; i < word.length() ; i ++)
                res.append(codes[word.charAt(i) - ‘a‘]);

            set.add(res.toString());
        }

        return set.size();
    }
}

View Code