纳税义务人和扣缴义务人

Posted 2021-03-07 bitzhuwei

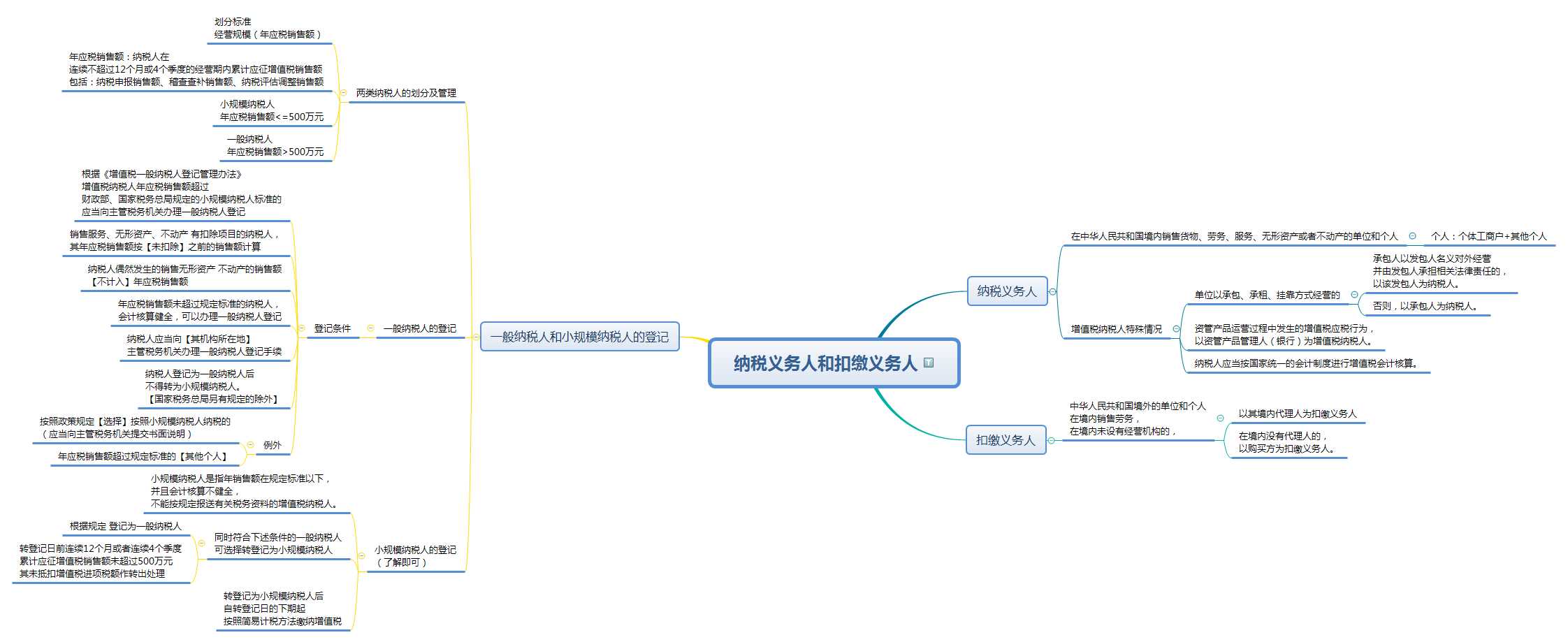
纳税义务人和扣缴义务人

 

资本论
市场上的商品
【市场】是频繁普遍地交换劳动产品的场所。只有在频繁普遍发生的情况下，才会存在经济规律。具有统计学意义的经济现象才能体现出经济规律，正如在光子的数量的足够多时，才能表现出波动性。频繁普遍，是本文所有经济现象的隐含形容词。
在市场上用于交换的劳动产品，是商品。
商品有【使用价值】和【价值】2种属性。 使用价值 是物理的、大自然方面的属性，它使商品有用。使用价值 不同，使得商品有交换的必要。价值 是社会的属性，劳动创造价值，消耗相等劳动量的商品，其价值相等，因此才能（双方心甘情愿地长期交地）交换。
劳动量可以以劳动时间计量。显然这个劳动时间的意思，是指社会平均劳动时间（否则就不符合频繁普遍的前提）。试想，某笨蛋1天做出来1双草鞋，刘备1天做出来8双，市场上大多数普通人1天做出来4双。如果市场上1双草鞋能卖1个金币。那么普通人会得到4个金币，刘备会得到8个，笨蛋只能得到1个。也就是说，刘备的劳动时间（创造的价值量）是普通人的2倍，是笨蛋的8倍。
吃大锅饭的错误，就在于让刘备和笨蛋都劳动一天，却都得到4个金币，这显然是不公平的，不得人心的，不能普遍频繁发生的，即必然销声匿迹的。
货币
金是商品。我用金买东西的时候，我没有提供对方直接需要使用的商品(除非他恰巧需要使用金做首饰)，我卖商品的时候，我没有得到我直接需要使用的商品。买和卖，就被金这个一般等价物分割开了。为什么偏偏是金做这个一般等价物？因为金的物理属性最适宜做一般等价物，它可分割，可融合，体积小，不怕酸碱不生锈不腐烂，容易称量，世界各地都有一定储量，千万年来 价值 稳定。因此金成为货币。
纸币是金的纸质符号。用纸币，就不需要每次都直接用金做买卖，更便捷安全。交易额也不受金总量的限制，因为可以超发纸币，印刷机印就行了。电子货币，连印刷都省了，没有密码，钱就不会丢失被盗，纸币的细菌传播被避免了，找零方便了，国家管理货币量更简单快捷了。如果政府信用破产，纸币就仅仅是纸，电子货币就仅仅是电脑里的一个数据了。
资本
人类消耗使用价值/价值，同时也在创造使用价值/价值。显然，创造的量＞消耗的量，否则怎么会有灯火辉煌高楼林立杀伐征战纸醉金迷？
如果养活劳动力一天需要3个饼，那么劳动力一天的价值就是3个饼的价值。劳动力的使用价值，就是创造价值。劳动力创造的价值(v+m)＞劳动力的价值v。资本家无偿获得了剩余价值m，因此暴富。
资本=原材料c＋劳动力v=＞产品(c+v+m)=新资本。用于这个生产再生产循环的资金，才是资本，埋在地下的金银纸币，最多是被封印休眠的资本。
资本就是现实世界的吸血鬼，它唯一的生存之道，就是不停地吸取剩余劳动m。
问：同样一家公司，利润由老板占有，老板发财。为何是被老板占有？因为老板是股东。如果公司里每个人都是股东呢？那就大家一起发财。为什么一般员工不当股东？因为他们没有初始资本，穷得只剩自己的劳动力可卖了。可见，想致富，要存储，无股份，不享福福。
如果人工智能能够 彻底 代替某个产业的所有人工劳动，那么此产业的产品就不再有价值，就会像树叶制造的氧气那样，成为免费或接近免费的东西。当然，如果资本家将此智能产业的产品据为己有，还是可以卖一段时间的钱的，只不过就不公平了，会和大锅饭一样最终销声匿迹。如果人工智能产业的产品仍然需要长期地花钱买，那只能是因为，所谓的人工智能仍旧需要程序员去更新维护，即仍然要投入人的劳动，即仍然具有 价值 这一属性。
价值的扭曲
资本追求的是 ROE=利润/资本 的最大化。ROE=m/(c+v)。
不同的行业里，c和v的比例是不同的。c的比例更大的行业，其价格就要高于价值（例如高科技企业，航空企业），否则，这个行业的资本家就吃亏了，不干了。反之亦然，c的比例小的行业（例如我国的小商品），其价格只能低于价值，否则，大量资本家会涌入这个行业，进而拉低其价格。资本追求最高利润率的不懈努力，使得各个行业的ROE，保持着动态平衡。这个平衡点上的ROE，就是平均ROE。
资本之死
如果劳动力一天工作8小时，养活自己的价值是2小时的劳动，那么m/v=6/2。显然，资本家会穷尽一切办法增加m降低v，所以才会不懈努力地推动科技和生产力的发展。
随着生产力的发展，c的比例会越来越大，所以 平均ROE 会越来越小。也就是说，资本家会发现，科技越发达，生产力越先进，他们就越难以找到好的投资机会。当生产力极度发达，资本就无法存活了，资本主义就会变成社会主义。只是这一天，到底需要多么强大的生产力呢？那般强大的生产力，存在吗？