机器学习第二周-模型评价（I）

Posted 2021-03-06 mindy-snail

    对于新建的模型，如何评价其好坏，以及自身的泛化能力，是机器学习中一个关键性问题。对于二分类模型，因原始数据可能是非平衡的，因此仅通过最后的预测准确率并不能评价模型的效果，对于机器学习中的分类与回归两大类模型，需采用不同的模型评价指标。

一?分类模型

 1．混淆矩阵及F1分数

    混淆矩阵（confusion matrix）实际是一张表格，因其能够很容易的看出机器学习有没有将样本的类别给混淆，故称之为混淆矩阵，以下为二分类的问题为例，其对应的混淆矩阵如下：

 

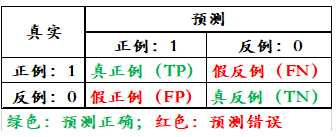
     正例为positive，负例为negative，横轴为预测值，纵轴为真实值

    TP：True Positive 真正例，表示预测值和真实值都为正例的个数

    TN：True Negative 真反例，表示与测值和真实值都为反例的个数

    FP：False Positive 假正例，表示真实值为反例，但是把他预测成了正例

    FN：False Negative 假反例 表示真实值是真例，但是把他预测成了反例

    准确率（Accuracy）ACC预测正确的个数比上总的个数，即分类模型所有判断正确的结果占总观测值的比重，准确率的表达式为：

      ACC=(TP+TN)/(TP+TN+FP+FN)

    精确率也叫查准率（precision）PPV，主要是针对正例来说的，就是预测正例的准确性，其公式为预测为正例且实际为正例的个数比上所有预测为正例个数，即在模型预测是Positive的所有结果中，模型预测对的比重，表达式为：

PPV=TP/(TP +FP)

    召回率（Recall）TPR也叫查全率灵敏度，预测正例预测正确的数目比上实际当中证实的正例的个数，在真实值是Positive的所有结果中，模型预测对的比重，表达式为：

TPR=TP/(TP+FN)

    精确率与召回率是一对相互矛盾的指标，精确率高的时候，召回率往往偏低，准确率低的时候，召回率往往偏高，主要是因FP与FN是互补的关系，精确率高了，FP的值就相应的低了，而FP值低了，FN的值就会提高。

    特异度（Specificity）TNR，是预测的反例在所有反例中的占比，在真实值是Negative的所有结果中，模型预测对的比重，其表达式为：

TNR=TN/(TN +FP)

 

    F1 是统计学中用来衡量二分类模型精确度的一种指标，同时兼顾了分类模型的精确率及召回率。F1分数可以看做是精确率和召回率的一种加权平均，其最大值为1，最小值为0,1代表模型的输出最好，0代表模型的输出结果最差。

F1=2PR/(P+R)

    其中P代表精确率PPV，C代表召回率TPR。

2．ROC与AUC 

    ROC（Receiver Operating Characteristic）受试者工作特征ROC是从医学上借鉴过来的概念。描述TPR和FPR之间的关系。X轴是FPR，Y轴是TPR。TPR就是所有正例中，有多少被正确地判定为正；FPR是所有反例中，有多少被错误地判定为正。

    分类阈值，即设置判断样本为正例的分界值，如果某个逻辑回归模型对某封电子邮件进行预测时返回的概率为 0.9995，则表示该模型预测这封邮件非常可能是垃圾邮件。相反，在同一个逻辑回归模型中预测分数为 0.0003 的另一封电子邮件很可能不是垃圾邮件。但若某封电子邮件的预测分数为 0.6 呢？为了将逻辑回归值映射到二元类别，必须指定分类阈值（也称为判定阈值）。如果值高于该阈值，则表示“垃圾邮件”；如果值低于该阈值，则表示“非垃圾邮件”。人们往往会认为分类阈值应始终为 0.5，但阈值取决于具体问题，应结合实际情况对其进行调整。在sklearn中有一个方法叫：decision_function，即返回分类阈值。

decision_scores=log_reg.decision_function(X_test)
y_predict = np.array(decision_scores >= 5, dtype=‘int‘)

       分类阈值取不同值，TPR和FPR的计算结果也不同，最理想情况下，我们希望所有正例与反例都被成功预测 TPR=1，FPR=0，即所有的正例预测值 > 所有的反例预测值，此时阈值取最小正例预测值与最大反例例预测值之间的值即可。

    ROC曲线距离左上角越近，证明分类器效果越好。如果算法1的ROC曲线完全包含算法2，则可以断定性能算法1>算法2。这很好理解，此时任做一条横线（纵线），任意相同TPR（FPR）时，算法1的FPR更低（TPR更高），故显然更优。

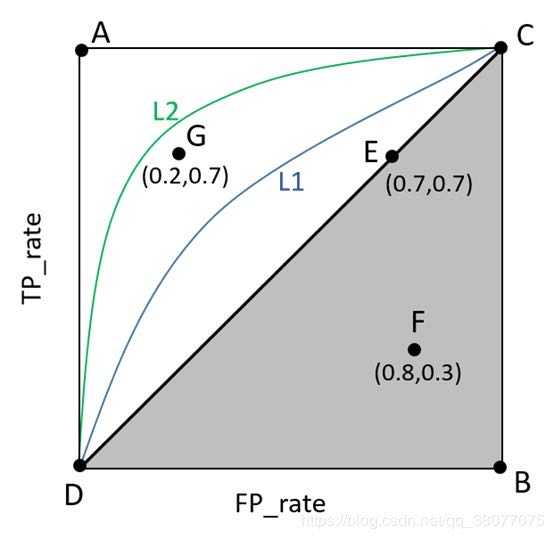
    从上面ROC图中的几个标记点，我们可以直观看出,左上角的点(TPR=1,FPR=0)，为完美分类，即医生医术高明，诊断全对。点G(TPR>FPR)，说明医生G的判断大体是正确的。中线上的点E(TPR=FPR)，也就是医生E的诊断全都是蒙的，蒙对一半，蒙错一半；下半平面的点F(TPR<FPR)，这个医生说你有病，那么你很可能没有病，医生F的话我们要反着听，为真庸医。

   若两个分类器的ROC曲线交叉，无法判断哪个分类器性能更好，这时可以计算曲线下的面积AUC，作为性能度量。一般在ROC曲线中，我们关注的是曲线下面的面积， 称为AUC（Area Under Curve）。AUC是横轴范围（0,1 ），纵轴是（0,1）所以总面积是小于1的，可以通过AUC直观评价模型的好坏。 

• • AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
  • 0.5 < AUC < 1，优于随机猜测。这个分类器妥善设定阈值的话，能有预测价值。
  • AUC = 0.5，跟随机猜测一样，模型没有预测价值。
  • AUC < 0.5，比随机猜测还差。

3．KS值 

    KS值是在模型中用于区分预测正负样本分隔程度的评价指标。每个样本的预测结果化为概率或者一个分数范围。从最小的概率或者最低分到最大的概率或者最高分，正负样本的累积分布。KS值为两个分布中，最大差值的绝对值。KS曲线是两条线，其横轴是阀值，纵轴是TPR（上面那条）与FPR（下面那条）的值，值范围[0,1]。两条曲线之间相相距最远的地方对应的阀值，就是最能划分模型的阀值。KS指标越高，模型的区分能力越强。

二、回归模型

1.简单评价指标

    平均绝对误差MAE是指预测值与真实值之间平均相差多大，能更好的反应预测误差值的真实情况。

    均方误差MSE是观察值与真实值偏差的平方和与观察次数的比值，也是线性回归中最常见的损失函数，线性回归过程中尽量让损失函数最小。同时MSE也可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。

    R-Square决定系数是通过数据的变化来表征一个拟合的好坏，正常取值范围[0,1]，越接近1，表明模型的变量对于y的解释能力越强，这个模型对数据拟合的效果也越好；越接近0，表明模型拟合的越差，经验值大于0.4，拟合效果好。但是数据集的样本越大，R方越大，因此不同数据集的模型结果比较会有一定的误差。

2.拟合优度常用其他指标

   赤池信息准则AIC，建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性，可以在参数数量和拟合能力之间权衡分析。增加自由参数的数目提高了拟合的优良性，AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合的情况，所以优先考虑的模型应是AIC值最小的那一个。假设在n个模型中做出选择，可一次算出n个模型的AIC值，并找出最小AIC值相对应的模型作为选择对象。赤池信息准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型。

   BIC是与AIC一样是对模型的拟合效果进行评价的一个指标，BIC值越小，则模型对数据的拟合越好。

   Hosmer–Lemeshow（The Hosmer–Lemeshow test）是评价logistic regression models拟合优度的常用方法，常在风险预测模型中使用。

三、交叉验证

   交叉验证，也称作循环估计，是一种统计学上将数据样本切割成较小子集的实用方法，该理论是由Seymour Geisser提出的。在给定的建模样本中，拿出大部分样本进行建模型，留小部分样本用刚建立的模型进行预报，并求这小部分样本的预报误差，记录它们的平方加和。这个过程一直进行，直到所有的样本都被预报了一次而且仅被预报一次。把每个样本的预报误差平方加和，称为PRESS(predicted Error Sum of Squares)。
　 交叉验证的基本思想是把在某种意义下将原始数据进行分组,一部分做为训练集(train set)，另一部分做为验证集(validation set or test set)。首先用训练集对分类器进行训练，再利用验证集来测试训练得到的模型(model)，以此来做为评价分类器的性能指标。下图是五折交叉验证，供参照理解。

　　无论分类还是回归模型，都可以利用交叉验证，进行模型评估，示例代码：

from sklearn.cross_validation import cross_val_score
print(cross_val_score(knn, X_train, y_train, cv=5))
print(cross_cal_score(lr, X, y, cv=5))

     以上是针对分类及回归模型评价指标的归纳，因时间原因，实际的操作是在下周补充并添加，留作以后回顾参照。