tarjan算法 求所有联通分量

Posted 2021-03-04 pangbi

摘自：https://blog.csdn.net/qq_34374664/article/details/77488976  （感谢)

tarjan算法，之所以用DFS就是因为它将每一个强连通分量作为搜索树上的一个子树。而这个图，就是一个完整的搜索树。
为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进行。每个点都有两个参数。
1，DFN［］作为这个点搜索的次序编号（时间戳），简单来说就是 第几个被搜索到的。％每个点的时间戳都不一样％。
2，LOW［］作为每个点在这颗树中的，最小的子树的根，每次保证最小，like它的父亲结点的时间戳这种感觉。如果它自己的LOW［］最小，那这个点就应该从新分配，变成这个强连通分量子树的根节点。
ps：每次找到一个新点，这个点LOW［］＝DFN［］。

而为了存储整个强连通分量，这里挑选的容器是，堆栈。每次一个新节点出现，就进站，如果这个点有 出度 就继续往下找。直到找到底，每次返回上来都看一看子节点与这个节点的LOW值，谁小就取谁，保证最小的子树根。如果找到DFN［］＝＝LOW［］就说明这个节点是这个强连通分量的根节点（毕竟这个LOW［］值是这个强连通分量里最小的。）最后找到强连通分量的节点后，就将这个栈里，比此节点后进来的节点全部出栈，它们就组成一个全新的强连通分量。

首先来一张有向图。网上到处都是这个图。我们就一点一点来模拟整个算法。

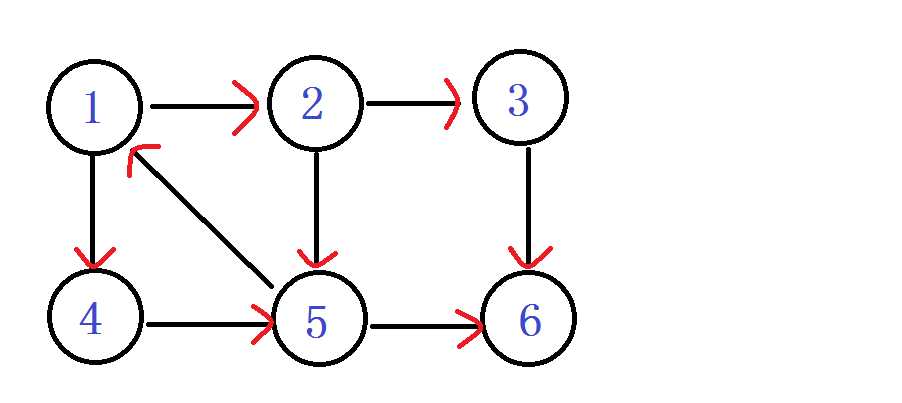
从1进入 DFN［1］＝LOW［1］＝ ＋＋index －－－－1
入栈 1
由1进入2 DFN［2］＝LOW［2］＝ ＋＋index －－－－2
入栈 1 2
之后由2进入3 DFN［3］＝LOW［3］＝ ＋＋index －－－－3
入栈 1 2 3
之后由3进入 6 DFN［6］＝LOW［6］＝＋＋index －－－－4
入栈 1 2 3 6

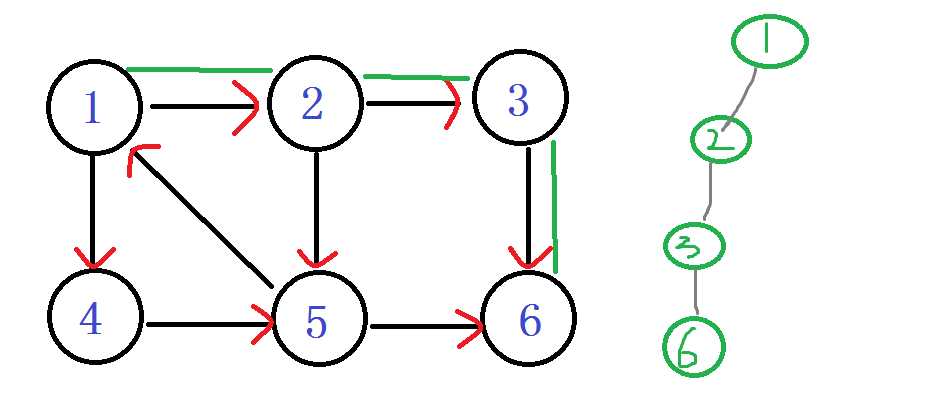
之后发现 嗯？ 6无出度，之后判断 DFN［6］＝＝LOW［6］
说明6是个强连通分量的根节点：6及6以后的点 出栈。
栈： 1 2 3 
之后退回 节点3 Low[3] = min(Low[3], Low[6]) LOW［3］还是 3
节点3 也没有再能延伸的边了，判断 DFN［3］＝＝LOW［3］
说明3是个强连通分量的根节点：3及3以后的点 出栈。
栈： 1 2 
之后退回 节点2 嗯？！往下到节点5
DFN［5］＝LOW［5］＝ ＋＋index －－－－－5
入栈 1 2 5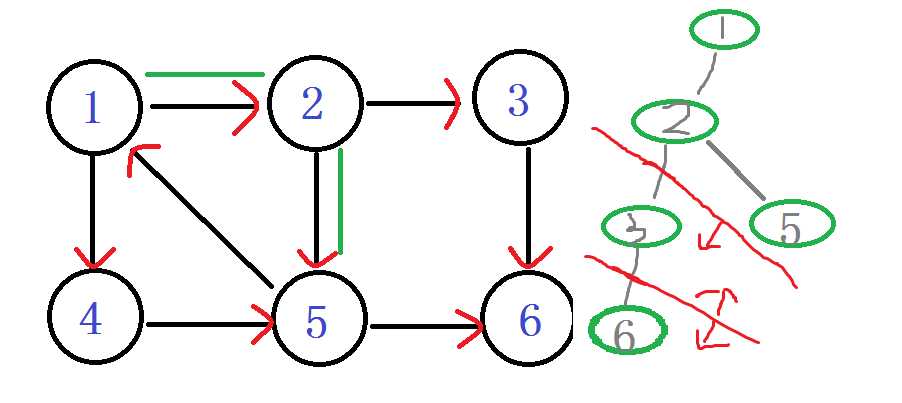

ps：你会发现在有向图旁边的那个丑的（划掉）搜索树 用红线剪掉的子树，那个就是强连通分量子树。每次找到一个。直接。一剪子下去。半个子树就没有了。。

结点5 往下找，发现节点6 DFN［6］有值，被访问过。就不管它。
继续 5往下找，找到了节点1 他爸爸的爸爸。。DFN［1］被访问过并且还在栈中，说明1还在这个强连通分量中，值得发现。 Low[5] = min(Low[5], DFN[1]) 
确定关系，在这棵强连通分量树中，5节点要比1节点出现的晚。所以5是1的子节点。so
LOW［5］＝ 1

由5继续回到2 Low[2] = min(Low[2], Low[5])
LOW［2］＝1；
由2继续回到1 判断 Low[1] = min(Low[1], Low[2]) 
LOW［1］还是 1
1还有边没有走过。发现节点4，访问节点4
DFN［4］＝LOW［4］＝＋＋index －－－－6
入栈 1 2 5 4 
由节点4，走到5，发现5被访问过了，5还在栈里，
Low[4] = min(Low[4], DFN[5]) LOW［4］＝5
说明4是5的一个子节点。

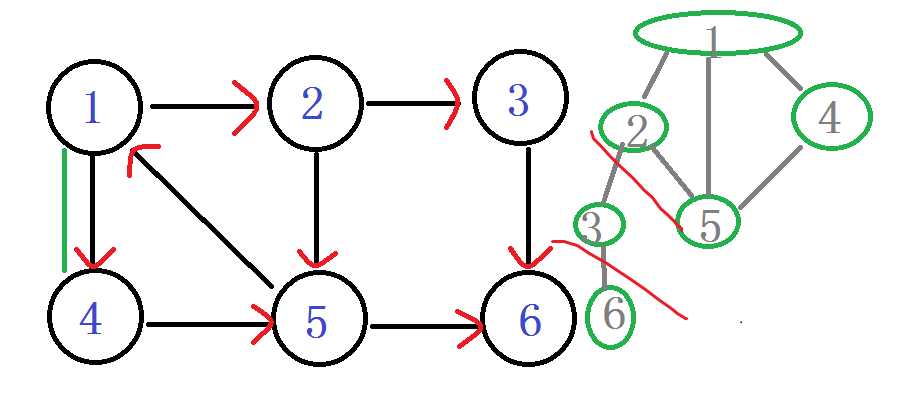
由4回到1.

回到1，判断 Low[1] = min(Low[1], Low[4])
LOW［1］还是 1 。

判断 LOW［1］ ＝＝ DFN［1］ 
诶？！相等了    说明以1为根节点的强连通分量已经找完了。
将栈中1以及1之后进栈的所有点，都出栈。
栈 ：（鬼都没有了）

这个时候就完了吗？！

你以为就完了吗？！

然而并没有完，万一你只走了一遍tarjan整个图没有找完怎么办呢？！

所以。tarjan的调用最好在循环里解决。

like    如果这个点没有被访问过，那么就从这个点开始tarjan一遍。

因为这样好让每个点都被访问到。

 1 #include<cstdio>
 2  #include<algorithm>
 3  #include<string.h>
 4  using namespace std;
 5  struct node {
 6      int v,next;
 7  }edge[1001];
 8   int DFN[1001],LOW[1001];
 9  int stack[1001],heads[1001],visit[1001],cnt,tot,index;
10 void add(int x,int y)
11 {
12      edge[++cnt].next=heads[x];
13      edge[cnt].v = y;
14      heads[x]=cnt;
15     return ;
16  }
17  void tarjan(int x)//代表第几个点在处理。递归的是点。
18  {
19      DFN[x]=LOW[x]=++tot;// 新进点的初始化。
20      stack[++index]=x;//进站
21      visit[x]=1;//表示在栈里
22     for(int i=heads[x];i!=-1;i=edge[i].next)
23      {
24          if(!DFN[edge[i].v]) {//如果没访问过
25             tarjan(edge[i].v);//往下进行延伸，开始递归
26              LOW[x]=min(LOW[x],LOW[edge[i].v]);//递归出来，比较谁是谁的儿子／父亲，就是树的对应关系，涉及到强连通分量子树最小根的事情。
27         }
28         else if(visit[edge[i].v ]){  //如果访问过，并且还在栈里。
29              LOW[x]=min(LOW[x],DFN[edge[i].v]);//比较谁是谁的儿子／父亲。就是链接对应关系
30          }
31      }
32      if(LOW[x]==DFN[x]) //发现是整个强连通分量子树里的最小根。
33     {
34          do{
35             printf("%d ",stack[index]);
36              visit[stack[index]]=0;
37              index--;
38          }while(x!=stack[index+1]);//出栈，并且输出。
39          printf("
");
40      }
41      return ;
42  }
43  int main()
44  {
45      memset(heads,-1,sizeof(heads));
46      int n,m;
47      scanf("%d%d",&n,&m);
48     int x,y;
49      for(int i=1;i<=m;i++)
50      {
51          scanf("%d%d",&x,&y);
52         add(x,y);
53      }
54     for(int i=1;i<=n;i++)
55          if(!DFN[i])  tarjan(i);//当这个点没有访问过，就从此点开始。防止图没走完
56     return 0;
57  }