人工智能导论A*算法求解八数码问题

Posted 2021-03-03 vivlalib

A*算法是一种启发式搜索算法，它的关键在于，每次从open表中选取结点时，要按特定的策略选取。该策略如下所述：

　　引入估值函数, f(n)是结点n的函数，f(n)越小，就意味着从初始状态节点S通过结点n的路径长度的估值最短。简而言之，f(n)越小，则通过结点n的路径是最佳路径的可能性越大。

 

　　因此，从open表中选取结点之前，我们先以f(n)为指标对open表中的所有节点进行排序，然后选取f(n)最小者即可。

　　　　具体地，在本题中

 

 

 

 

 

以下是完整代码

  1 # from queue import Queue
  2 from 八数码问题BFS import move0  # move0函数参考上一篇博文：https://www.cnblogs.com/vivlalib/p/12557518.html
  3 import numpy as np
  4 import time
  5 
  6 class Node:
  7     def __init__(self, state, parent, operator):
  8         self.state = state
  9         self.parent = parent
 10         self.operator = operator
 11     def operate(self, dir):  # 操作算符
 12         new_state = move0(self.state, dir)
 13         if new_state is False:
 14             return None
 15         else:
 16             return Node(new_state, self, dir)  # 以self为父
 17     def islegal(self):  # 检查结点的合法性, 根据实际问题改变
 18         return self
 19     def traverse(self):
 20         cur = self
 21         res = []
 22         while cur is not None:
 23             # print(cur.state)
 24             res.append(cur)
 25             cur = cur.parent
 26         # res.pop()
 27         return res
 28     def depth(self):  # 当前结点到根节点的距离，根据实际问题改变
 29         return len(self.traverse()) - 1
 30 
 31 def findn(state, n):  # 在state中寻找n的位置
 32     for i in range(len(state)):
 33         for j in range(len(state)):
 34             if state[i][j] == n:
 35                 ind0 = [i, j]
 36     return ind0
 37 def manhattan(pos1, pos2):  # pos1, pos2 are like [x, y]
 38     return abs(pos1[0] - pos2[0]) + abs(pos1[1] - pos2[1])
 39 
 40 
 41 def distance0(state1, state2):  # 自己乱写的距离函数，很慢  15s
 42     state1 = np.array(state1)
 43     state2 = np.array(state2)
 44     ret = np.sum(np.abs(state1-state2))  # ∑|state1[i] - state2[i]|  对应维度差的绝对值之和，即曼哈顿距离
 45     return ret
 46 
 47 def distance(state1, state2):  # 这里使用曼哈顿距离,  0.21s
 48 
 49     posn1, posn2 = [], []
 50     for n in range(9):  # 分别在state1与state2中查找0到9的位置
 51         posn1.append(findn(state1, n))
 52         posn2.append(findn(state2, n))
 53     dsum = 0
 54     for i in range(9):
 55         dsum += manhattan(posn1[i], posn2[i])
 56     return dsum
 57 
 58 
 59 
 60 
 61 def f(node:Node, goal_state):  # 估价函数
 62     """
 63     公式表示为： f(n)=g(n)+h(n),
 64     其中 f(n) 是从初始点经由节点n到目标点的估价函数，
 65     g(n) 是在状态空间中从初始节点到n节点的实际代价，
 66     h(n) 是从n到目标节点最佳路径的估计代价。
 67     :param node:
 68     :return:
 69     """
 70     cur_state = np.array(node.state)
 71     goal_state = np.array(goal_state)
 72     gn = node.depth()
 73     hn = distance(cur_state, goal_state)
 74     return gn + hn
 75 
 76 
 77 def showinfo(node: Node):  # 用于搜索成功后的输出
 78     nlist = node.traverse()
 79     nlist.reverse()
 80     for n in nlist:
 81         if n.operator is not None:
 82             print(n.operator)
 83         print(n.state)
 84 
 85 
 86 def Astar(init_state, goal_state):
 87     dirs = [‘up‘, ‘down‘, ‘left‘, ‘right‘]
 88     open = []  # open表
 89     closed = []
 90     root = Node(init_state, None, None)  # 起始状态，根节点
 91     open.append(root)
 92     while open:  # 若open表为空，退出循环
 93         open.sort(key=lambda x: f(x, goal_state))
 94         node = open.pop(0)  # 选出open表中f(n)最小者
 95         closed.append(node)
 96         # 扩展
 97         for dir in dirs:
 98             node_tmp = node.operate(dir)  # 以dir为方向拓展结点
 99             # 新节点合法
100             if node_tmp is not None and node_tmp not in closed:
101                 open.append(node_tmp)
102                 if node_tmp.state == goal_state:  # node_tmp 是目标结点？
103                     print(‘搜索成功。‘)
104                     showinfo(node_tmp)
105                     return True
106     return False
107 
108 goalss = [[1, 2, 3],
109         [8, 0, 4],
110         [7, 6, 5]]
111 goal = [[2,0,3],
112         [1,8,4],
113         [7,6,5]]
114 init = [[2,8,3],
115         [1,0,4],
116         [7,6,5]]
117 
118 goal = [[1, 2, 3],
119         [8, 0, 4],
120         [7, 6, 5]]
121 
122 init = [[2,8,0],
123         [1,6,3],
124         [7,5,4]]
125 if __name__ == ‘__main__‘:
126 
127     print(Astar(init,goal))
128     print(time.process_time())

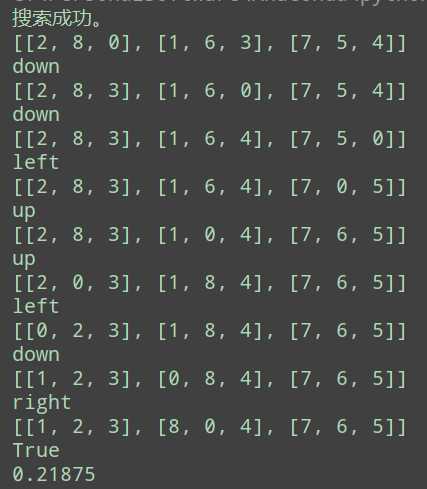
运行结果如下：