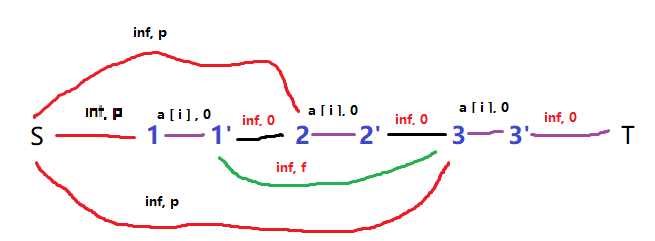
一个餐厅在相继的 NN 天里,每天需用的餐巾数不尽相同。假设第 ii 天需要 r_iri?块餐巾( i=1,2,...,N)。餐厅可以购买新的餐巾,每块餐巾的费用为 pp 分;或者把旧餐巾送到快洗部,洗一块需 m 天,其费用为 f 分;或者送到慢洗部,洗一块需 nn 天(n>mn>m),其费用为 ss 分(s<fs<f)。
每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。
试设计一个算法为餐厅合理地安排好 NN 天中餐巾使用计划,使总的花费最小。编程找出一个最佳餐巾使用计划。
#include <bits/stdc++.h>
using namespace std;
#define int long long
template<class T>inline void read(T &res)
{
char c;T flag=1;
while((c=getchar())<‘0‘||c>‘9‘)if(c==‘-‘)flag=-1;res=c-‘0‘;
while((c=getchar())>=‘0‘&&c<=‘9‘)res=res*10+c-‘0‘;res*=flag;
}
const int MAXN = 2e3 + 5;
const int inf = 0x3f3f3f3f;
int N;
struct Edge{
int to, val, cost;
Edge *next, *ops;
Edge(int to, int val, int cost, Edge *next): to(to), val(val), cost(cost), next(next){}
};
Edge *head[MAXN << 1];
void BuildGraph(int u, int v, int w, int c) {
head[u] = new Edge(v, w, c, head[u]);
head[v] = new Edge(u, 0, -c, head[v]);
head[u]->ops = head[v]; head[v]->ops = head[u];
}
namespace zkw{
int s, t, ans, res;
int dis[MAXN << 1];
bool vis[MAXN << 1];
bool Spfa() {
memset(vis, false, sizeof vis);
memset(dis, 0x3f, sizeof dis);
deque<int> q;
q.push_back(s);
vis[s] = true; dis[s] = 0;
while (!q.empty()) {
int u = q.front(); q.pop_front(); vis[u] = false;
for (Edge *e = head[u]; e; e = e->next) {
int v = e->to;
if (e->val > 0 && dis[u] + e->cost < dis[v]) {
dis[v] = dis[u] + e->cost;
if (!vis[v]) {
vis[v] = true;
if (!q.empty() && dis[v] < dis[q.front()]) q.push_front(v);
else q.push_back(v);
}
}
}
}
return dis[t] < inf;
}
int Dfs(int u, int flow) {
if (u == t) {
vis[u] = true;
res += flow;
return flow;
}
int used = 0; vis[u] = true;
for (Edge *e = head[u]; e; e = e->next) {//当前弧就不加了
int v = e->to;
if ((!vis[v] || v == t) && e->val && dis[u] + e->cost == dis[v]) {
int mi = Dfs(v, min(e->val, flow - used));
if (mi) {
e->val -= mi;
e->ops->val += mi;
ans += e->cost * mi;
used += mi;
}
if (used == flow) break;
}
}
return used;
}
void Work() {
res = 0; ans = 0;
while (Spfa()) {
vis[t] = true;
while (vis[t]) {
memset(vis, false, sizeof vis);
Dfs(s, inf);
}
}
}
}
signed main() {
read(N);
zkw :: s = 0; zkw :: t = N * 2 + 1;
int s = 0, t = 2 * N + 1;
for ( int i = 1; i <= N; ++i ) {
int x; read(x);
BuildGraph(s, i, x, 0);
BuildGraph(i + N, t, x, 0);
}
int p, m, f, n, S;
read(p); read(m); read(f); read(n); read(S);
for ( int i = 1; i <= N; ++i ) {
BuildGraph(s, i + N, inf, p);
if(i + m <= N)
BuildGraph(i, i + N + m, inf, f);
if(i + n <= N)
BuildGraph(i, i + N + n, inf, S);
if(i + 1 <= N)
BuildGraph(i, i + 1, inf, 0);
}
zkw :: Work();
cout << zkw :: ans << endl;
return 0;
}