数据科学流程之创建新特征

Posted 2021-03-03 guojiaxue

当特征和目标变量不是很相关时，可以修改输入的数据集，应用线性，非线性变换（或者其他相似方法）来提高系统的精度。

- 数据是“死”的，人的思维是“活”的。

- 数据科学家负责改变数据集和输入数据，使数据更好的符合分类模型。

基本方法：
A. 特征的线性修正

B. 特征的非线性修正

K近邻方法（K-Nearset neighbors,KNN）

K近邻算法思路：

　　在特征空间中，如果一个样本附近的k个最近（即特征空间中最邻近）样本的大多数属于某一个类别，则该样本也属于这个类别。

K邻近算法步骤：

　　在分类过程中仅需要在训练集中寻找最近（基于欧氏距离或其他的距离度量）的前K个样本，然后在这K个最相似样本中出现最多的目标标号就被选为分类标号。

参数：

邻近数目K；

估计相似度的度量（常用的是欧氏距离，L2距离）。

A 特征线性修正

例：加利福尼亚州的房价数据集（california_housing）分析

目标变量是房子价格（实数）——回归问题

注：

回归问题是连续型数据，分类问题是离散性数据

(1) 从sklearn工具包中加载数据——Python命令直接加载

In[1]:
1 import numpy as np
2 from sklearn.datasets import fetch_california_housing
3 housing = fetch_california_housing()
4 housing

Out[1]:
{‘data‘: array([[   8.3252    ,   41.        ,    6.98412698, ...,    2.55555556,
           37.88      , -122.23      ],
        [   8.3014    ,   21.        ,    6.23813708, ...,    2.10984183,
           37.86      , -122.22      ],
        [   7.2574    ,   52.        ,    8.28813559, ...,    2.80225989,
           37.85      , -122.24      ],
        ...,
        [   1.7       ,   17.        ,    5.20554273, ...,    2.3256351 ,
           39.43      , -121.22      ],
        [   1.8672    ,   18.        ,    5.32951289, ...,    2.12320917,
           39.43      , -121.32      ],
        [   2.3886    ,   16.        ,    5.25471698, ...,    2.61698113,
           39.37      , -121.24      ]]),
 ‘target‘: array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894]),
 ‘feature_names‘: [‘MedInc‘,
  ‘HouseAge‘,
  ‘AveRooms‘,
  ‘AveBedrms‘,
  ‘Population‘,
  ‘AveOccup‘,
  ‘Latitude‘,
  ‘Longitude‘],
 ‘DESCR‘: ‘.. _california_housing_dataset:

California Housing dataset
--------------------------

**Data Set Characteristics:**

    :Number of Instances: 20640

    :Number of Attributes: 8 numeric, predictive attributes and the target

    :Attribute Information:
        - MedInc        median income in block
        - HouseAge      median house age in block
        - AveRooms      average number of rooms
        - AveBedrms     average number of bedrooms
        - Population    block population
        - AveOccup      average house occupancy
        - Latitude      house block latitude
        - Longitude     house block longitude

    :Missing Attribute Values: None

This dataset was obtained from the StatLib repository.
http://lib.stat.cmu.edu/datasets/

The target variable is the median house value for California districts.

This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).

It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.

.. topic:: References

    - Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
      Statistics and Probability Letters, 33 (1997) 291-297
‘}

这里的‘feature_name‘是特征名，有房龄，人均面积，人均房间数，人均卧室数，能容纳多少人等等信息；‘data‘是二维数组(特征数据数组)，包含了每个房子的具体信息，如房甲可以容纳3人，20平，20年等；‘target‘是一维数组(目标数组或标签数组)，包含了房子的价格。

1 X=housing[‘data‘]
2 Y=housing[‘target‘]

1 #将原始数据按照比例分割为“测试集”和“训练集”
2 from sklearn.model_selection import train_test_split
3 X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.8)

 (2-1)计算均方误差

　　均方差（Mean Squared Error，MSE）是参数估计值与真实值之差的平方的期望值。MSE的值越小，说明预测模型描述实验数据的准确度更好。

　　　

 

1 from sklearn.neighbors import KNeighborsRegressor
2 from sklearn.metrics import mean_squared_error
3 regressor = KNeighborsRegressor()#建立一个K邻近模型
4 regressor.fit(X_train,Y_train)#将训练集的两部分进行拟合（建模）
5 Y_est = regressor.predict(X_test)#对测试集预测得到Y_est
6 print("MSE=",mean_squared_error(Y_test, Y_est))#利用均方误差将观察结果和预测结果进行模型评估

MSE= 1.1570134432841734

注：每次运行可能获得的MSE值都不一样，因为将原始数据进行分割时，虽然是按照比例2：8分割；但是是随机分割，每次分到的数据值都有所不同。

注：MAE和MSE的区别

平均绝对误差（Mean Absolute Error，MAE）是所有单个观测值与算术平均值的偏差的绝对值的平均。

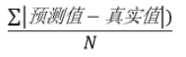
1 from sklearn.metrics import mean_absolute_error
2 print("MAE=",mean_absolute_error(Y_test,Y_est))

MAE= 0.8234513512596899

(2-2)计算均方误差——Z-scores标准化

　　Z-scores标准化是将特征映射为均值为0，标准差为1的新特征，使原始数据转换为无量纲化值，即各指标值都处于同一数量级别（均值为0，标准差为1的级别）。也就是求每一列的均值，然后用原始数据减去均值再除以方差。

1 from sklearn.preprocessing import StandardScaler#标准化
2 scaler = StandardScaler()
3 X_train_scaled = scaler.fit_transform(X_train)#先拟合数据，再把其转换成标准形式（也就是为了得到特征值的均值和方差，即转换规则）
4 X_test_scaled = scaler.transform(X_test)#把测试数据标准化（因为上一步已经拟合过建好了模型，就不需要再次拟合了，直接标准化就行了）
5 regressor = KNeighborsRegressor()#K邻近模型
6 regressor.fit(X_train_scaled,Y_train)#把标准化之后的新特征和Y_train进行拟合
7 Y_est = regressor.predict(X_test_scaled)#对标准化的测试特征值预测
8 print("MSE",mean_squared_error(Y_test,Y_est))

MSE 0.4485372399520397

第一步：导入sklearn包；

第二步：实例化出一个scaler；

第三步：利用.fit_transform(trainData)先拟合数据，得到均值和方差，再转换为标准形式；（抽象理解为X轴上是数据，Y轴上是标准化后（均值为0方差为1）的数据）

第四步：利用.transform(testData)把测试数据标准化；

第五步：实例化K邻近模型；

第六步：利用K邻近模型里的.fit()函数拟合标准化数据和训练集的标签数据；

第七步：利用模型.predict()函数对标准化测试集进行预测；

第八步：计算观测值和预测值的均方误差。

标准化之后，均方差值减小一半。

注：Z-scores标准化属于线性变换。

（2-3）计算均方误差——鲁棒性缩放

　　鲁棒性缩放（RobustScaler）采用中位数和IQR对每个特征进行单独缩放。IQR：第一个和第三个四分位数。

　　由于数据读入缺失，传输错误或传感器损坏等原因，如果有一个或一些点远离中心，这些异常数据对均值和方差的影响较大，但对中位数和四分位数影响不大，因此鲁棒缩放对于异常值更

1 from sklearn.preprocessing import RobustScaler
2 scaler2 = RobustScaler()
3 X_train_scaled = scaler2.fit_transform(X_train)
4 X_test_scaled = scaler2.transform(X_test)
5 regressor = KNeighborsRegressor()
6 regressor.fit(X_train_scaled,Y_train)
7 Y_est = regressor.predict(X_test_scaled)
8 print("MSE=",mean_squared_error(Y_test,Y_est))

MSE= 0.44666046843260077

注：鲁棒缩放属于线性变换。

- 通过比较标准化的MSE和鲁棒缩放的MSE可以判断该数据集内异常数据多少。假如标准化MSE>鲁棒缩放MSE就可以得出该数据集异常数据较多的结论，反之相反。

B 特征非线性修正

　　假定输出结果与房屋居住人数大致相关（但不是线性相关）：

　　- 事实上，房屋是1个人住还是3个人住，其价格会有很大区别。

　　- 然而，同样的房子10个人居住和12个人居住，其价格差别并不是很大（尽管仍然是两个人的差别）

我们可以将房屋利用率的平方根作为新特征

平方根特点：当数据比较小的时候，变化比较大；当数据比较大的时候，变化比较小。

 1 non_linear_feat = 5 #AvgOccup平均占用率是第六个特征。索引从0开始。
 2 X_train_new_feat = np.sqrt(X_train[:,non_linear_feat])#将训练集第6列整个取出求平方根
 3 X_train_new_feat.shape = (X_train_new_feat.shape[0],1)#将行数，列数存入
 4 X_train_extended = np.hstack([X_train,X_train_new_feat])#堆栈数组水平顺序（列），将新特征列存入数据集

 5 X_test_new_feat = np.sqrt(X_test[:,non_linear_feat])
 6 X_test_new_feat.shape = (X_test_new_feat.shape[0],1)
 7 X_test_extended = np.hstack([X_test,X_test_new_feat])

 8 scaler = StandardScaler()
 9 X_train_extended_scaled = scaler.fit_transform(X_train_extended)
10 X_test_extended_scaled = scaler.transform(X_test_extended)
11 regressor = KNeighborsRegressor()
12 regressor.fit(X_train_extended_scaled,Y_train)
13 Y_est = regressor.predict(X_test_extended_scaled)
14 print("MSE=",mean_squared_error(Y_test,Y_est))

MSE= 0.3796934162768246

注：sqrt()属于非线性变换。

我们可以看到这次的MSE又小了，说明我们这次特征的非线性变换很有效。