拯救大兵瑞恩

Posted 2021-02-27 jjl0229

链接

https://www.acwing.com/problem/content/1133/

题目

1944 年，特种兵麦克接到国防部的命令，要求立即赶赴太平洋上的一个孤岛，营救被敌军俘虏的大兵瑞恩。

瑞恩被关押在一个迷宫里，迷宫地形复杂，但幸好麦克得到了迷宫的地形图。

迷宫的外形是一个长方形，其南北方向被划分为 N 行，东西方向被划分为 M 列， 于是整个迷宫被划分为 N×M 个单元。

每一个单元的位置可用一个有序数对 (单元的行号, 单元的列号) 来表示。

南北或东西方向相邻的 2 个单元之间可能互通，也可能有一扇锁着的门，或者是一堵不可逾越的墙。

注意： 门可以从两个方向穿过，即可以看成一条无向边。

迷宫中有一些单元存放着钥匙，同一个单元可能存放 多把钥匙，并且所有的门被分成 P 类，打开同一类的门的钥匙相同，不同类门的钥匙不同。

大兵瑞恩被关押在迷宫的东南角，即 (N,M) 单元里，并已经昏迷。

迷宫只有一个入口，在西北角。

也就是说，麦克可以直接进入 (1,1) 单元。

另外，麦克从一个单元移动到另一个相邻单元的时间为 1，拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。

试设计一个算法，帮助麦克以最快的方式到达瑞恩所在单元，营救大兵瑞恩。

输入格式
第一行有三个整数,分别表示 N,M,P 的值。

第二行是一个整数 k，表示迷宫中门和墙的总数。

接下来 k 行，每行包含五个整数，(X_{i1},Y_{i1},X_{i2},Y_{i2},G_i)：当 Gi≥1 时，表示 ((X_{i1},Y_{i1})) 单元与 ((X{i2}2,Y{i2})) 单元之间有一扇第 (G_i) 类的门，当 Gi=0 时，表示 ((X_{i1},Y_{i1})) 单元与 ((X{i2}2,Y{i2})) 单元之间有一面不可逾越的墙。

接下来一行，包含一个整数 S，表示迷宫中存放的钥匙的总数。

接下来 S 行，每行包含三个整数 (X_{i1},Y_{i1},Q_i)，表示 ((X_{i1},Y_{i1})) 单元里存在一个能开启第 (Q_i) 类门的钥匙。

输出格式
输出麦克营救到大兵瑞恩的最短时间。

如果问题无解，则输出 -1。

数据范围
(|X_{i1}?X_{i2}|+|Y_{i1}?Y_{i2}|=1,)
(0≤G_i≤P,)
(1≤Q_i≤P,)
(1≤N,M,P≤10,)
(1≤k≤150)
输入样例：

4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0 
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2 
4 2 1

输出样例：

14

样例解释：
迷宫如下所示：

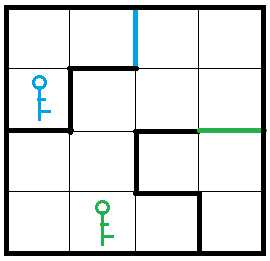
思路

状压DP和bfs。n,m,s都很小。预处理每个格子上有的钥匙种类，以及方格之间的门和墙。然后从(0,0)开始跑bfs，储存每个点的位置和钥匙，f[x][y][s]表示在(x,y)点有钥匙s的状态，对于每个点去更新它可以到达的点和具有钥匙的状态的最短距离。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=10,inf=0x3f3f3f3f;
int n,m,p;
int id(int x,int y){
    return m*(x)+y;
}
int g[N*N][N*N]; //-1不通过 0通过 1~有门
int gg[N][N]; //0没钥匙
struct ac{
    int x,y,s,c;
    bool operator<(const ac &b) const {
        return c<b.c;
    }
};
int f[N][N][1<<N];
priority_queue<ac>  q;
int X[]={0,0,-1,1};
int Y[]={1,-1,0,0};
int bfs(){
    memset(f,inf,sizeof f);
    f[0][0][gg[0][0]]=0;
    q.push((ac){0,0,gg[0][0],0});
    while(!q.empty()){
        int x=q.top().x,y=q.top().y,s=q.top().s;q.pop();
        for(int i=0;i<4;++i){
            int xx=x+X[i],yy=y+Y[i],ss=(s|gg[xx][yy]);
            if(xx<0||xx>=n||yy<0||yy>=m||g[id(x,y)][id(xx,yy)]==-1) continue;
            if(  (g[id(x,y)][id(xx,yy)]&s)  ||  g[id(x,y)][id(xx,yy)]==0 ) {
                if(f[x][y][s]+1<f[xx][yy][ss]){
                    f[xx][yy][ss]=f[x][y][s]+1;
                    q.push((ac){xx,yy,ss,f[xx][yy][ss]});
                }
            }
        }
    }
    int ans=inf;
    for(int i=0;i<(1<<p); ++i){
        ans=min(ans,f[n-1][m-1][i]);
    }
    return ans;
}
int main(){
    cin>>n>>m>>p;
    int k;
    cin>>k;
    while(k--){
        int x1,y1,x2,y2,t;

        cin>>x1>>y1>>x2>>y2>>t;
        x1--,y1--,x2--,y2--;

        if(t==0){
            g[id(x1,y1)][id(x2,y2)]=-1;
            g[id(x2,y2)][id(x1,y1)]=-1;
        }
        else {
            --t;
            g[id(x1,y1)][id(x2,y2)]|=(1<<t);
            g[id(x2,y2)][id(x1,y1)]|=(1<<t);
        }
    }
    int s;
    cin>>s;
    while(s--){
        int x,y,t;
        cin>>x>>y>>t;
        --x,--y,--t;
        gg[x][y]|=(1<<t);
    }
    int ans=bfs();
    if(ans==inf) cout<<"-1";
    else cout<<ans<<endl;
    return 0;
}