二叉树总结树的遍历

Posted 2020-09-08

该文我会用来总结二叉树相关的知识

二叉树如下图：

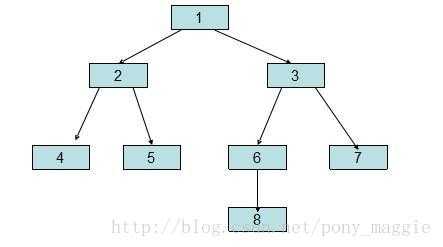
二叉树的结构

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

二叉树构造方法

为了测试二叉树的的各种算法，我不得不写一个二叉树的构造方法，我主要是用层次遍历的方式来构造二叉树的。层次遍历在后面会详细说到。

用字符串的方式来输入二叉树的序列，例如：

输入：1 2 3 4 5 6 7 null null null null null 8 null null

以上输入都是字符，最后两个null可省略。

 1 TreeNode *createBinaryTree(vector<string> &arr){
 2     TreeNode *head = NULL;
 3     if (!arr.at(0).compare("null"))return head;//空树
 4     queue<TreeNode *>Q;
 5     vector<string>::iterator it = arr.begin();
 6     head = new TreeNode(stringToInteger(*it++));//stringToInteger将string转为int
 7     TreeNode *p = NULL;
 8     Q.push(head);//树根入队
 9     //队列不空，且没超过arr的大小（用于arr最后多余的null未列出来的情况,即上面说的可省略的情况）
10     while (!Q.empty() && it != arr.end()){
11         p = Q.front();//取出队首元素
12         Q.pop();
13         if (!(*it).compare("null")){//arr序列的下一个为空,则左子树为空
14             p->left = NULL;
15         }
16         else{//否则生成左子树
17             p->left = new TreeNode(stringToInteger(*it));
18             Q.push(p->left);//左子树入队
19         }
20         ++it;
21         if (it == arr.end())break;//不忘判断arr是否越界
22         if (!(*it).compare("null")){//arr序列的下一个为空,则右子树为空
23             p->right = NULL;
24         }
25         else{//否则生成右子树
26             p->right = new TreeNode(stringToInteger(*it));
27             Q.push(p->right);//右子树入队
28         }
29         ++it;
30     }
31     return head;
32 }

用数值的方式来输入二叉树的序列，例如：

输入：1 2 3 4 5 6 7 -1 -1 -1 -1 -1 8

默认树的所有值都是大于0的。

TreeNode *createBinaryTree(const vector<int> &arr){
    int index = 0;
    queue<TreeNode *>Q;
    TreeNode *head = new TreeNode(arr.at(index++));
    Q.push(head);
    TreeNode *p = NULL;
    while (index < arr.size() && !Q.empty()){
        p = Q.front();
        Q.pop();
        if (arr.at(index) >= 0){
            TreeNode *temp = new TreeNode(arr.at(index));
            p->left = temp;
            Q.push(temp);
        }
        ++index;
        if (index >= arr.size())break;
        if (arr.at(index) >= 0){
            TreeNode *temp = new TreeNode(arr.at(index));
            p->right = temp;
            Q.push(temp);
        }
        ++index;
    }
    return head;
}

二叉树遍历方法

前序遍历：1->2->4->5->3->6->8->7

中序遍历：4->2->5->1->8->6->3->7

后序遍历：4->5->2->8->6->7->3->1

层次遍历：1->2->3->4->5->6->7->8

前序递归实现：

 1 vector<int> preorder(TreeNode* root){
 2     vector<int> retInt;
 3     if (root == NULL)return retInt;//空树
 4     retInt.push_back(root->val);//先访问值
 5     vector<int> left = preorder(root->left);//进入左子树
 6     retInt.insert(retInt.end(), left.begin(), left.end());//复制左子树的访问结果
 7     vector<int> right = preorder(root->right);//进入右子树
 8     retInt.insert(retInt.end(), right.begin(), right.end());
 9     return retInt;
10 }

前序费递归实现：

 1 vector<int> preorder(TreeNode* root){
 2     vector<int>retInt;
 3     if (root == NULL)return retInt;//空树
 4     stack<TreeNode *>s;
 5     s.push(root);//树根入栈
 6     while (!s.empty()){
 7         TreeNode *p = s.top();
 8         retInt.push_back(p->val);//先访问值
 9         if (p->left != NULL){
10             s.push(p->left);//遍历左子树，左子树入栈
11         }
12         else{//左子树为空
13             s.pop();//当前节点出栈
14             while (p->right == NULL && !s.empty()){//寻找非空右子树
15                 p = s.top();
16                 s.pop();
17             }
18             if (p->right != NULL)s.push(p->right);//右节点入栈
19         }
20     }
21     return retInt;
22 }

中序递归实现：

1 vector<int> inorder(TreeNode* root){
2     vector<int> retInt;
3     if (root == NULL)return retInt;//空树
4     retInt = inorder(root->left);//遍历左子树
5     retInt.push_back(root->val);//访问当前节点值
6     vector<int> temp = inorder(root->right);//遍历右子树
7     retInt.insert(retInt.end(),temp.begin(),temp.end());//复制右子树的结果
8     return retInt;
9 }

中序非递归实现：

 1 vector<int> inorder(TreeNode* root){
 2     vector<int> retInt;
 3     if (root == NULL) return retInt;//空树
 4     TreeNode *p = NULL;
 5     stack<TreeNode *> s;
 6     s.push(root);//树根入栈
 7     while (!s.empty()){
 8         p = s.top();//获取栈顶元素
 9         if (p->left != NULL){
10             s.push(p->left);//其左子树入栈
11         }
12         else{//左子树为空时
13             s.pop();
14             retInt.push_back(p->val);//访问其节点值
15             while (p->right == NULL && !s.empty()){//寻找非空右子树
16                 p = s.top();//若右子树为空，获取新的栈顶元素
17                 retInt.push_back(p->val);//访问新元素的值
18                 s.pop();
19             }
20             if (p->right != NULL)s.push(p->right);//右子树入栈
21         }
22     }
23     return retInt;
24 }

后序的递归实现：

1 vector<int> postorderTraversal2(TreeNode* root){
2     vector<int> retInt;
3     if (root == NULL)return retInt;//空树
4     retInt = preorderTraversal2(root->left);//进入左子树
5     vector<int> right = preorderTraversal2(root->right);//进入右子树
6     retInt.insert(retInt.end(), right.begin(), right.end());
7     retInt.push_back(root->val);//最后访问值
8     return retInt;
9 }

后序的非递归实现：

 

总结：

前序、中序、后序

用法：

LeetCode的Binary Tree Inorder Traversal可用中序遍历来检查，二叉搜索树的中序遍历结果是递增的。