立体视觉—计算视差图
Posted twzh123456
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了立体视觉—计算视差图相关的知识,希望对你有一定的参考价值。
一、立体视觉简介
1、立体视觉的研究背景及意义
立体视觉是计算机视觉领域的一个重要课题,它的目的在于重构场景的三维几何信息。立体视觉的研究具有重要的应用价值,其应用包括航空及遥感测量,工业自动化系统等。
立体视觉的研究方法之一,利用多幅图象来恢复三维信息的方法,它是被动方式的。根据图象获取方式的区别又可以划分成普通立体视觉和通常所称的光流(optical flow)两大类。普通立体视觉研究的是由两摄像机同时拍摄下的两幅图象,而光流法中研究的是单个摄像机沿任一轨道运动时顺序拍下的两幅或更多幅图象。前者可以看作后者的一个特例,它们具有相同的几何构形,研究方法具有共同点。双目立体视觉是它的一个特例。
2、立体匹配算法的基本实现思想
该算法是基于灰度的匹配算法,这是一种区域相关方法, 在一幅图象中以一点为中心选定一区域(窗口),在另一幅图象中寻找与该区域相关系数最大的区域,把该找到的区域的中心认为是原来那区域中心的对应点。它对噪声很敏感,所以需要搭配去噪滤波使用。
二、视差图计算
1、什么是视差图
视差图是以图像对中任一幅图像为基准,其大小为该基准图像的大小,元素值为视差值的图像。由于视差图包含了场景的距离信息,因此从立体图像对中提取视差图的图像匹配,一直是双目视觉研究中最为活跃的领域,值得我们去深度的学习。
2、NCC方法计算视差图
NCC是归一化相关性(normalization cross-correlation)的简称,NCC,就是用于归一化待匹配目标之间的相关程度,比较的是原始像素。通过在待匹配像素位置p(px,py)构建匹配窗口,与目标像素位置p‘(px+d,py)同样构建邻域匹配窗口的方式建立目标函数来对匹配窗口进行度量相关性,注意这里构建相关窗口的前提是两帧图像之间已经校正到水平位置,即光心处于同一水平线上,此时极线是水平的,否则匹配过程只能在倾斜的极线方向上完成。度量方式由如下式子定义:
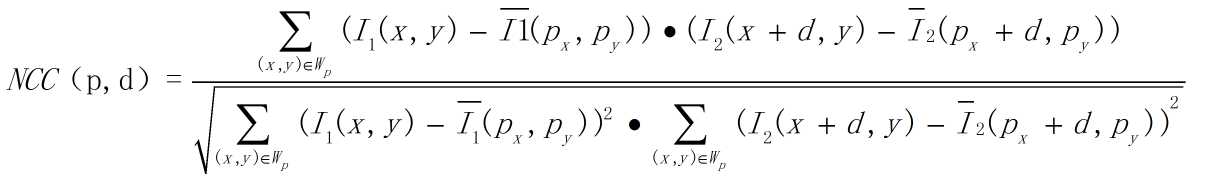
其中p点表示图像I1待匹配像素坐标(px,py),d表示在图像I2被查询像素位置在水平方向上与px的距离。左边为图像I1,右边为图像I2。左视图和右视图两幅图像大小相同,只有水平方向上的视角变换。
三、实验环境
Python + PyCharm
四、实验数据

图片下载地址为:http://vision.middlebury.edu/stereo/data/scenes2003/
五、实验步骤与结果展示
5.1 当窗口大小为3时,视差图如下:

分析:匹配窗口中出现很多不连续的点,图像边缘特征也很模糊。
5.2 当窗口大小为5时,视差图如下:

5.3 当窗口大小为7时,视差图如下:

5.4 当窗口大小为11时,视差图如下:

- 分析总结:从以上实验结果可以看出,当窗口值为3时视差匹配结果很模糊,基本看不清;把窗口值大小增大到5后,运行的匹配结果图片稍微清晰了一点,但仍无法看出图中是何物品,当真大窗口值后,可以很明显地看出,运行结果中的图片越来越靠近实物图像。所以,窗口值大小越大,视差图更清晰。但窗口值也不是越大运行结果就越清晰,当窗口值过大时,图片噪声也增多,从而使图片与实物图片相比更为杂乱,运行耗时越长。
六、实验总结
从以上对im2和im3的计算结果可以看出窗口值过小时,在低纹理区域出现误匹配,匹配精度较低,视差图特别模糊;随着窗口值增大,匹配区分度逐渐清晰,误匹配区域得到矫正,匹配精度随着窗口值增大而变高。但当窗口值过大时,在深度区域容易出现误匹配。窗口值过小时,匹配代价区分度过低,在低纹理区域容易出现误匹配,匹配精度较低;窗口值的大小应适中,不宜过大也不宜过小。随着窗口值增大,匹配区分度逐渐清晰,误匹配区域得到矫正,匹配精度随着窗口值增大而变高。
七、实验代码展示
# -*- coding: utf-8 -*- from PIL import Image from pylab import * import cv2 from numpy import * from numpy.ma import array from scipy.ndimage import filters def plane_sweep_ncc(im_l,im_r,start,steps,wid): """ 使用归一化的互相关计算视差图像 """ m,n = im_l.shape # 保存不同求和值的数组 mean_l = zeros((m,n)) mean_r = zeros((m,n)) s = zeros((m,n)) s_l = zeros((m,n)) s_r = zeros((m,n)) # 保存深度平面的数组 dmaps = zeros((m,n,steps)) # 计算图像块的平均值 filters.uniform_filter(im_l,wid,mean_l) filters.uniform_filter(im_r,wid,mean_r) # 归一化图像 norm_l = im_l - mean_l norm_r = im_r - mean_r # 尝试不同的视差 for displ in range(steps): # 将左边图像移动到右边,计算加和 filters.uniform_filter(np.roll(norm_l, -displ - start) * norm_r, wid, s) # 和归一化 filters.uniform_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, s_l) filters.uniform_filter(norm_r*norm_r,wid,s_r) # 和反归一化 # 保存 ncc 的分数 dmaps[:,:,displ] = s / sqrt(s_l * s_r) # 为每个像素选取最佳深度 return np.argmax(dmaps, axis=2) def plane_sweep_gauss(im_l,im_r,start,steps,wid): """ 使用带有高斯加权周边的归一化互相关计算视差图像 """ m,n = im_l.shape # 保存不同加和的数组 mean_l = zeros((m,n)) mean_r = zeros((m,n)) s = zeros((m,n)) s_l = zeros((m,n)) s_r = zeros((m,n)) # 保存深度平面的数组 dmaps = zeros((m,n,steps)) # 计算平均值 filters.gaussian_filter(im_l,wid,0,mean_l) filters.gaussian_filter(im_r,wid,0,mean_r) # 归一化图像 norm_l = im_l - mean_l norm_r = im_r - mean_r # 尝试不同的视差 for displ in range(steps): # 将左边图像移动到右边,计算加和 filters.gaussian_filter(np.roll(norm_l, -displ - start) * norm_r, wid, 0, s) # 和归一化 filters.gaussian_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, 0, s_l) filters.gaussian_filter(norm_r*norm_r,wid,0,s_r) # 和反归一化 # 保存 ncc 的分数 dmaps[:,:,displ] = s / np.sqrt(s_l * s_r) # 为每个像素选取最佳深度 return np.argmax(dmaps, axis=2) im_l = array(Image.open(r‘C:UsersAdministratorDesktopim2.png‘).convert(‘L‘), ‘f‘) im_r = array(Image.open(r‘C:UsersAdministratorDesktopim3.png‘).convert(‘L‘),‘f‘) # 开始偏移,并设置步长 steps = 40 start = 4 # ncc 的宽度 wid = 9 res = plane_sweep_ncc(im_l,im_r,start,steps,wid) import scipy.misc scipy.misc.imsave(‘depth.png‘,res) show() # -*- coding: utf-8 -*- from PIL import Image from pylab import * import cv2 from numpy import * from numpy.ma import array from scipy.ndimage import filters def plane_sweep_ncc(im_l,im_r,start,steps,wid): """ 使用归一化的互相关计算视差图像 """ m,n = im_l.shape # 保存不同求和值的数组 mean_l = zeros((m,n)) mean_r = zeros((m,n)) s = zeros((m,n)) s_l = zeros((m,n)) s_r = zeros((m,n)) # 保存深度平面的数组 dmaps = zeros((m,n,steps)) # 计算图像块的平均值 filters.uniform_filter(im_l,wid,mean_l) filters.uniform_filter(im_r,wid,mean_r) # 归一化图像 norm_l = im_l - mean_l norm_r = im_r - mean_r # 尝试不同的视差 for displ in range(steps): # 将左边图像移动到右边,计算加和 filters.uniform_filter(np.roll(norm_l, -displ - start) * norm_r, wid, s) # 和归一化 filters.uniform_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, s_l) filters.uniform_filter(norm_r*norm_r,wid,s_r) # 和反归一化 # 保存 ncc 的分数 dmaps[:,:,displ] = s / sqrt(s_l * s_r) # 为每个像素选取最佳深度 return np.argmax(dmaps, axis=2) def plane_sweep_gauss(im_l,im_r,start,steps,wid): """ 使用带有高斯加权周边的归一化互相关计算视差图像 """ m,n = im_l.shape # 保存不同加和的数组 mean_l = zeros((m,n)) mean_r = zeros((m,n)) s = zeros((m,n)) s_l = zeros((m,n)) s_r = zeros((m,n)) # 保存深度平面的数组 dmaps = zeros((m,n,steps)) # 计算平均值 filters.gaussian_filter(im_l,wid,0,mean_l) filters.gaussian_filter(im_r,wid,0,mean_r) # 归一化图像 norm_l = im_l - mean_l norm_r = im_r - mean_r # 尝试不同的视差 for displ in range(steps): # 将左边图像移动到右边,计算加和 filters.gaussian_filter(np.roll(norm_l, -displ - start) * norm_r, wid, 0, s) # 和归一化 filters.gaussian_filter(np.roll(norm_l, -displ - start) * np.roll(norm_l, -displ - start), wid, 0, s_l) filters.gaussian_filter(norm_r*norm_r,wid,0,s_r) # 和反归一化 # 保存 ncc 的分数 dmaps[:,:,displ] = s / np.sqrt(s_l * s_r) # 为每个像素选取最佳深度 return np.argmax(dmaps, axis=2) im_l = array(Image.open(r‘C:imageim3.png‘).convert(‘L‘), ‘f‘) im_r = array(Image.open(r‘C:imageim4.png‘).convert(‘L‘),‘f‘) # 开始偏移,并设置步长 steps = 40 start = 4 # ncc 的宽度 wid = 9 res = plane_sweep_ncc(im_l,im_r,start,steps,wid) import scipy.misc scipy.misc.imsave(‘depth.png‘,res) show()
以上是关于立体视觉—计算视差图的主要内容,如果未能解决你的问题,请参考以下文章