数据结构之排序算法

Posted 2021-02-20 zyj-0917

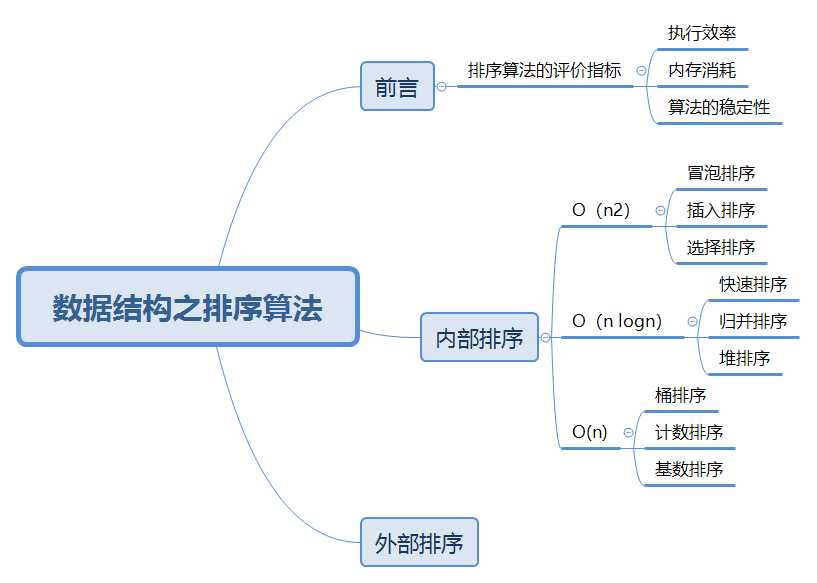
一、前言

排序算法的评价指标：

1. 算法执行效率

• 最好、最坏以及平均时间复杂度。注意：原始数据有序度的不同，对排序的执行时间有很大的影响
• 时间复杂度的系数、常数、低阶。注意：实际开发中，数据规模可能很小，因此需要考虑这几个方面
• 比较次数和交换次数。注意：基于比较的排序算法会涉两个基本的操作，即元素比较大小和元素交换或者移动

2.算法的内存消耗

• 引入原地排序(Sorted in place)，即原地排序算法，特指空间复杂度为O(1)

3.算法的稳定性

• 稳定性指原始原始数据集中存在两个相等的元素，在排序过后，两个元素的前后相对顺序不发生改变。不改变为稳定的排序，否则为不稳定的排序。

二、时间复杂度为O(n2)的排序算法

• 冒泡排序(Bubble Sort)

1. 核心思想：对相邻的两个元素进行比较，看是否满足大小关系要求。
2. 核心代码：

//排序方法
    public static void bubbleSort(int[] arr){
        //首先判断数组的大小
        if (arr.length <= 1){
            return;
        }
        for (int i = 0; i < arr.length - 1; i++) {//冒泡的趟数for (int j = 0; j < arr.length - 1 - i; j++) {//交换次数
                if (arr[j] > arr[j + 1]){
                    int temp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = temp;
                }
            }
        }
    }
重点：冒泡的次数i为：数组的长度n - 1；每次冒泡的比较次数j = n - i - 1
代码优化：

//优化的排序方法
    public static void bubbleSort(int[] arr){
        //首先判断数组的大小
        if (arr.length <= 1){
            return;
        }
        for (int i = 0; i < arr.length - 1; i++) {//冒泡的趟数
            boolean flag = false;//添加标志位，用于判断是否发生数据交换;若某一趟没有发生交换，说明后续数组已经有序，可以不用进行比较
            for (int j = 0; j < arr.length - 1 - i; j++) {//交换次数
                if (arr[j] > arr[j + 1]){
                    temp = arr[j + 1];
                    arr[j + 1] = arr[j];
                    arr[j] = temp;
　　                 flag = true;
                }
            }
            if(!flag){
                break;
            }
        }
    }

 

　　　　3.算法指标：

• 最好时间复杂度O(n)，即原始数组为有序的；最坏时间复杂度O(n2)，即原始数组为逆序的；
• 平均时间复杂度：因原始数组的有序性不同，分析比较复杂。引入“有序度”和“无序度”的概念。
• 有序度指的是具有有序关系的元素对的个数
• 完全无序的数组有序度为0；完全有序的数组有序度为n*(n-1)/2,即满有序度
• 逆序度与有序度相反。逆序度 = 满有序度 - 有序度。
• 排序的过程相当于增加有序度，减少无序度
• 平均时间复杂度取中间值。n*(n-1)/4,O(n2)
• 是原地排序算法
• 是稳定排序算法
• 插入排序（Insertion Sort）
• 核心思想：将未排序数组分为已排序区间和未排序区间。将未排序区间的元素与已排序区间的元素依次进行比较，进行插入
• 核心代码：

 1 public static void insertionSort(int[] arr){//默认从小到大，尾部比较法
 2         for (int i = 1; i < arr.length; i++) {//此时i代表的是未排序区间中要参与插入的元素以及其位置
 3             int value = arr[i];
 4             int j = i - 1;
 5             for (; j >= 0 ; j--) {//从尾部开始比较，j代表已排序区间的元素个数
 6                 if (arr[j] > value){
 7                     arr[j + 1] = arr[j];
 8                 }else{
 9                     break;
10                 }
11             }
12             arr[j + 1] = value;
13         }
14     }

//默认从大到小，头部插入法
for (int i = 1; i < arr.length; i++) {
    for (int j = 0; j < i ; j++) {
        if (arr[j] < arr[i]){
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
}
注意：若从小到大排序，则选择尾部插入法；从大到小排序，则选择头部插入法

• 算法指标
• 是稳定排序算法
• 是原地排序算法
• 最好：O(n)；最坏：O(n2)；平均时间复杂度：O(n2)
• 选择排序（Selection Sort）
• 核心思想：将数组分为待排序区间和已排序区间。从未排序区间中选择元素最小的元素，放到已排序区间的末尾
• 核心代码：

 1 public static void sectionSort(int[] arr){默认从小到大
 2         for (int i = 0; i < arr.length - 1; i++) {//比较后元素要插入的位置
 3             int min = arr[i];
 4             int minIndex = i;//用于存放最小值的坐标
 5             for (int j = i + 1; j < arr.length; j++) {//比较区间中最小的元素
 6                 if (min > arr[j]){
 7                     min = arr[j];
 8                     minIndex = j;
 9                 }
10             }
11             if (minIndex != i){
12                 arr[minIndex] = arr[i];
13                 arr[i] = min;
14             }
15         }
16     }

• 算法指标：
• 原地排序算法、非稳定算法
• 最好、最坏以及平均时间复杂度都为O(n2)
• 小结

1. 算法性能：插入排序 > 选择排序 > 冒泡排序
2. 三种算法都可以看作将排序区间分为待排序区间和已排序区间
3. 使用场景：小规模数据排序