《利用Swap Set分析风控模型更替的影响》

Posted 2021-02-20 cx2016

 

利用Swap Set分析风控模型更替的影响

 

 

风控业务背景

当你开发完成一个新模型，此时风控策略同学肯定会问——这一版模型相对于上一版模型有什么提升？因此，我们需要评估新模型与旧模型之间的性能差异。如果新模型的性能还不如旧模型，那也就没有替换旧模型的必要了（KPI也就堪忧 ）。

本文将介绍风控策略中常见的一种分析方法——Swap Set Analysis（交换集分析）。

目录
Part 1. Swap Set的初步认识
Part 2. 从通过率和坏账率评估模型的业务效果
Part 3. Swap Set的理解分析
Part 4. 如何开展拒绝推断？
致谢
版权声明
参考资料

Part 1. Swap Set的初步认识

在新旧模型更替过程中，不仅需要调整风控策略，更需要将新模型的价值最大化。这个分析过程可以通过Swap set实现。

Swap set refers to “swapping out” a set of customer accounts — generally bad accounts — and replacing them with, or “swapping in,” a set of good customer accounts.

在《信贷风控审批中的决策否决管理》一文中，我们知道信用评分模型使用时需要结合策略分析制定一个cutoff（及格分数线），通常高于这个cutoff会审批通过，否则予以拒绝（人工否决案例除外）。

因此，新旧两个模型都分别会制订一个cutoff，按是否被（新/旧）模型（拒绝/通过）为维度，两两交叉可形成一个矩阵，如图1所示。

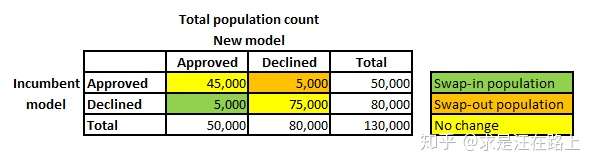图 1 - Swap Set矩阵

由此，客群可细分为3个子客群（segment），它们分别是：

• 1. Swap-in population：指旧模型拒绝但新模型接受的客户。
• 2. Swap-out population：指旧模型接受但新模型拒绝的客户。
• 3. No change：指同时被新旧模型拒绝或接受，因此审批状态没有差异。

Part 2. 从通过率和坏账率评估模型的业务效果

诚然，我们可以对比新旧模型的技术指标（AUC、KS、Gini等）来对比两者的差异，但是模型最终是用在风控策略中的。因此，我们从业务应用角度来评估模型性能更为合适。

通常情况下，通过率（approval rate）与坏账率（bad rate）之间是正相关的。通过率上升，往往带来坏账率上升。极端考虑：当通过率达到100%时，等同风控系统完全失效，此时坏账率将达到最大；当通过率为0%时，坏账率也能达到0%，但此时平台也将赚不到钱。

因此，这也就是风险管理的精髓所在——风险和收益同在，如何在通过率和坏账率之间寻找一个平衡点。

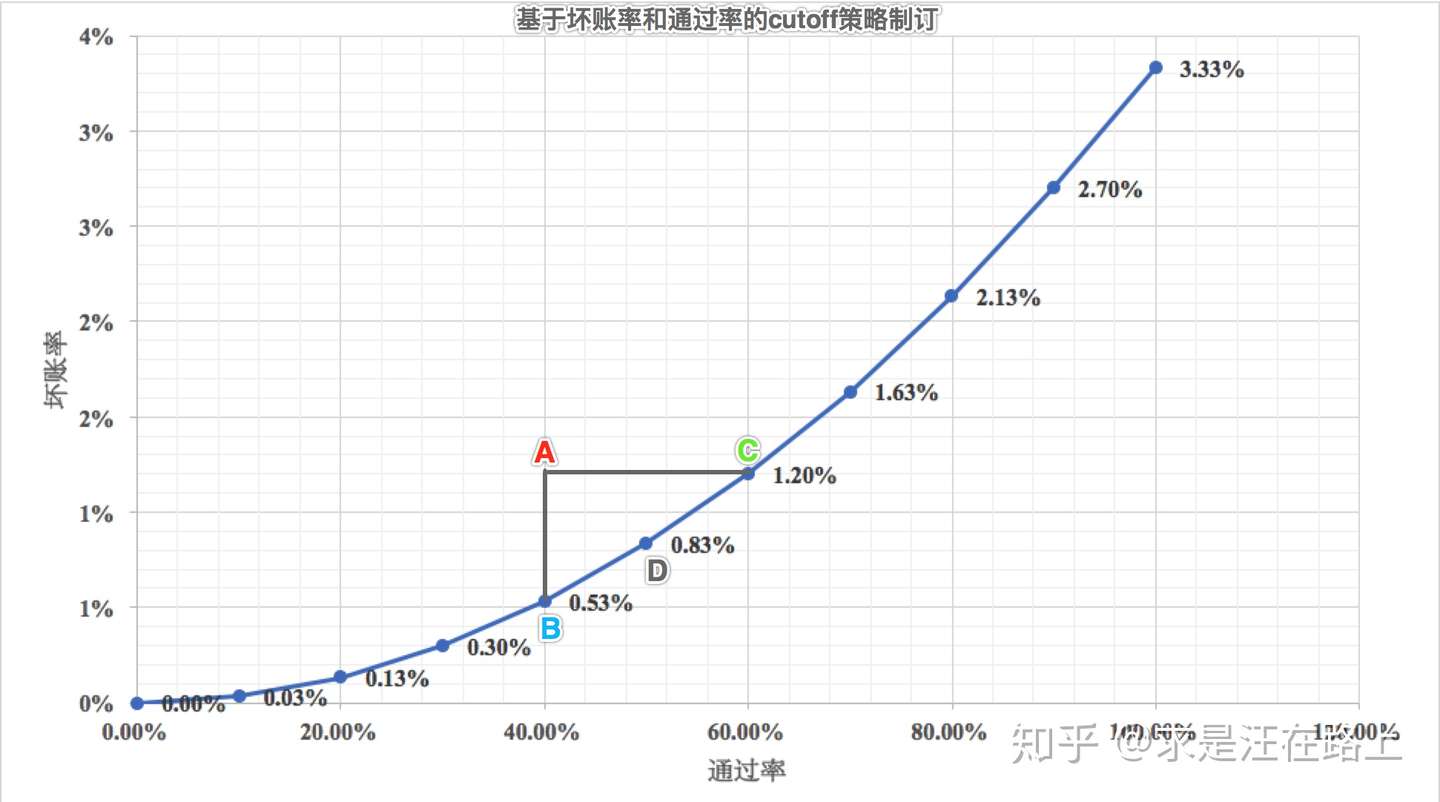图 2 - 基于坏账率和通过率的cutoff策略制订

如图2所示，如果当前策略（A点）：通过率40%，坏账率1.2%，那么在引入信用评分模型后，我们可以从2个临界点之间的任意一个位置作为新的策略目标，分别是：

B点：保持通过率在40%不变，坏账率由1.2%下降到0.53%；
C点：保持坏账率在1.2%不变，通过率由40%提高到60%；
D点：保证通过率提高到50%，同时坏账率下降到0.83%；

然而，坏账率较高的客群，由于风险定价也相应较高，带来的收益并一定会减少。相反，很多平台并没有把坏账率控制得多低，而是通过风险定价来获得很高的利润。例如，714高炮平台的通过率很高（通常> 50%），坏账率也很高，但其风险定价（借款1000，收砍头息200，到手800，7天后还款1000）极高，这还是能保证其得到暴利。

因此，我们可以从通过率和坏账率两个维度评估模型的业务性能。那么，对应到图1的swap set矩阵中，若满足以下几个场景，则可论证“新模型比旧模型表现更好”这一观点。

1. 场景一（对应B点）：Swap-in population = Swap-out population，即新模型和旧模型的通过率相同，但坏账率降低。
2. 场景二（对应C点）：Swap-in population > Swap-out population，即新模型相对于旧模型的通过率更高，但坏账率保持不变。
3. 场景三：Swap-in population = Swap-out population，即新模型和旧模型的通过率相同，且坏账率也相同，但用户响应率（response rate）提高。

Part 3. Swap Set的理解分析

我们知道，无论是放贷还是拒绝的客群中都有好坏客户，只是拒绝客群中bad rate相对于放贷客群中更高而已（ 这也是拒绝推断涉及的命题）。显然，我们希望Swap out更多的坏客户，Swap in更多的好客户。这也是Swap set的取名意义所在——拿坏人交换好人。

如图3所示，新模型从旧模型拒绝的人群中swap in进6个人（5个good，1个bad）至放贷，并swap out出6个人（3个bad，3个good）至拒绝。

在这个交换（swap）过程中，通过总人数不变（通过率不变，都为50%），但由于swap out比swap in多出2个bad，因此新模型的坏账率更低。

最终，旧模型拒绝和通过的人群中各有4个bad；而新模型拒绝人群中有6个bad，通过人群中只有2个bad。尽管通过率都是50%，但bad的分布已经发生了变化，导致坏账率降低。

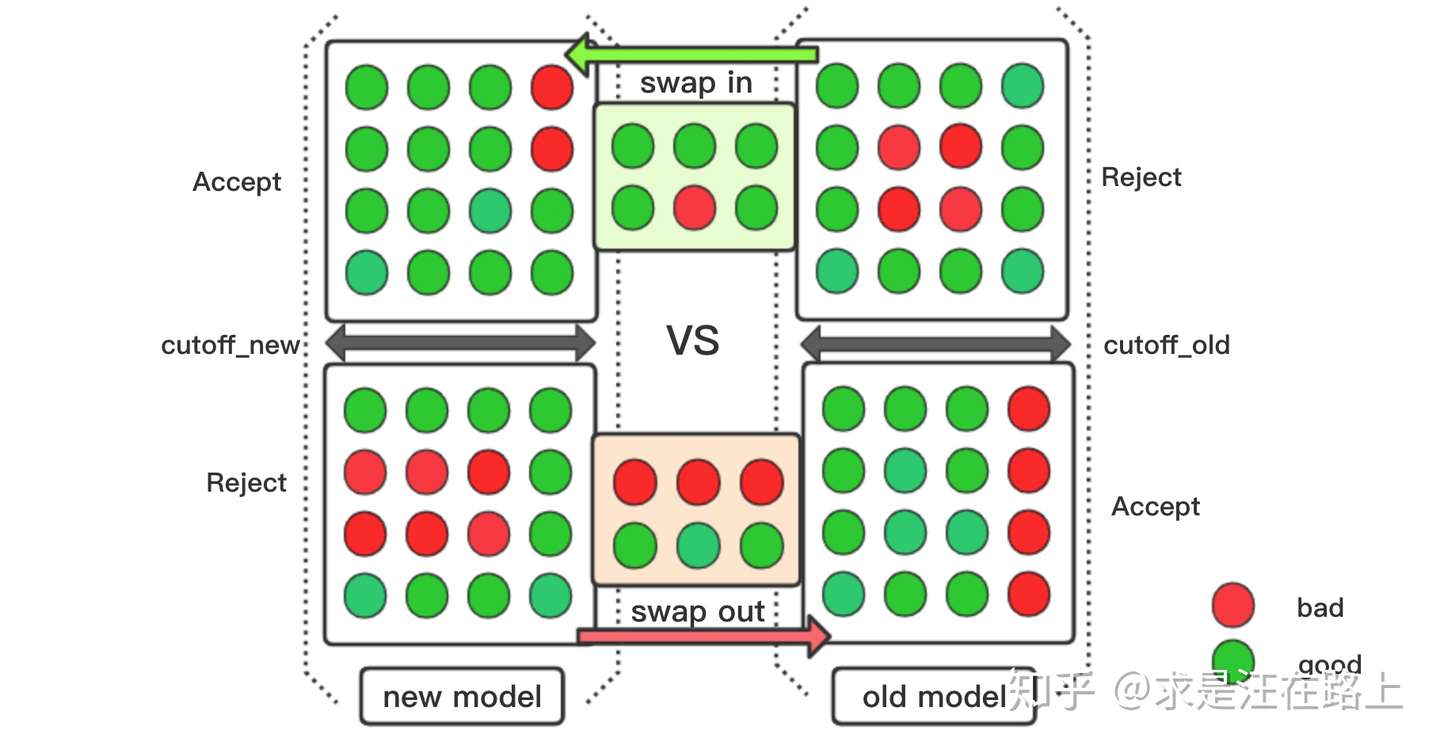图 3 - swap in 和 swap out的图解

为了更容易理解，我们在图1的基础上结合数字分析。我们执行以下步骤得到图4。

step1. 统计每个格子里的坏客户数（bads）。
step2. 除以每个格子里的总客户数（total），得到bad rate

在图1中可知，新旧模型的通过率都保持不变（38.4%），但是旧模型的坏账率为8.3%，而新模型的坏账率为4.9%。那么就可得出结论：

在通过率不变的前提下，新模型相对于旧模型显著降低了41%的坏账率！
其中： 41% =（4.9% - 8.3%）/ 8.3%

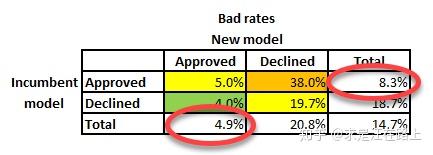图 4 - bad rate统计

Part 4. 如何开展拒绝推断？

在图4的计算过程中，我们会发现一个问题：对于旧模型拒绝的客户，我们并不能获知其好坏（贷后逾期表现）。此时只能采用一种近似的方式，也就是通过对照组来估计，或者称为拒绝推断（reject inference）。

方案1: 同时间窗不同尾号

如果上线策略时分尾号进行AB-Test，对A组（对照组）只打分不生效，B组（实验组）打分并生效。由于B组中低于cutoff的客户将会被策略拒绝，那么就可以从A组中低于cutoff的放贷客群的bad rate作为B组的近似估计。（is there any bias?）

方案2: 跨时间窗相同尾号

如果模型上线存在灰度期，那么在灰度阶段就是只打分不生效，因此可从这段灰度期中低于新模型cutoff的客群中计算bad rate，作为正式生效时对拦截客群的bad rate估计。当然，由于存在逾期好坏的表现期，如果只是对比首逾风险，也得至少有1个月的灰度期。